на листе клеточной тетради с помощью линейки
найти и изучить
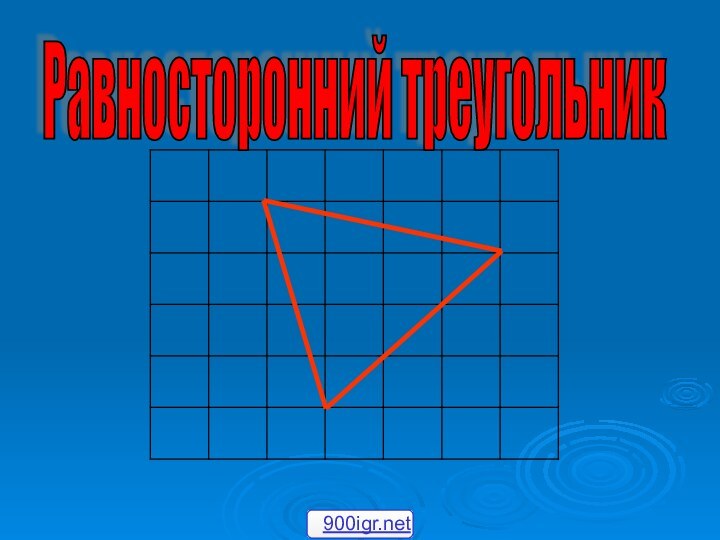
различные соотношения в равностороннем треугольникевыбрать наиболее интересные и представить их одноклассникам, и показать в своей работе
Цели работы
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









Цели работы
Как мы шли к этой цели?
A
B
C
P
E
L
F
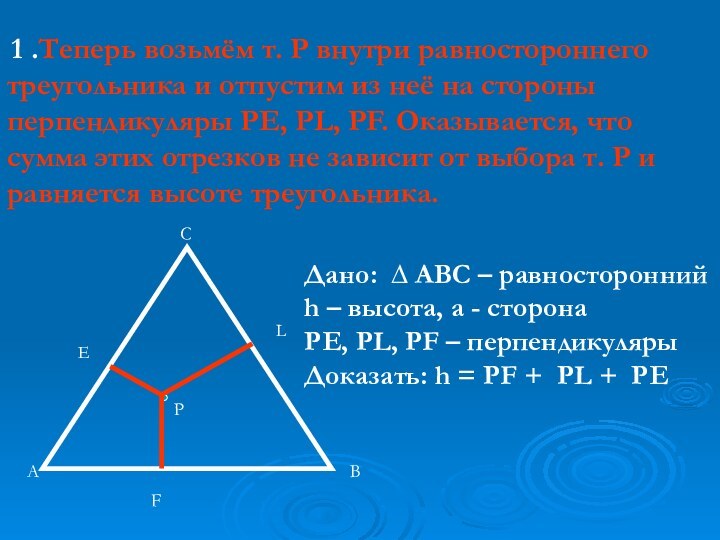
Дано: ∆ АВС – равносторонний
h – высота, a - сторона
РЕ, РL, PF – перпендикуляры
Доказать: h = РF + PL + PE
М
N
K
D
M
R
S
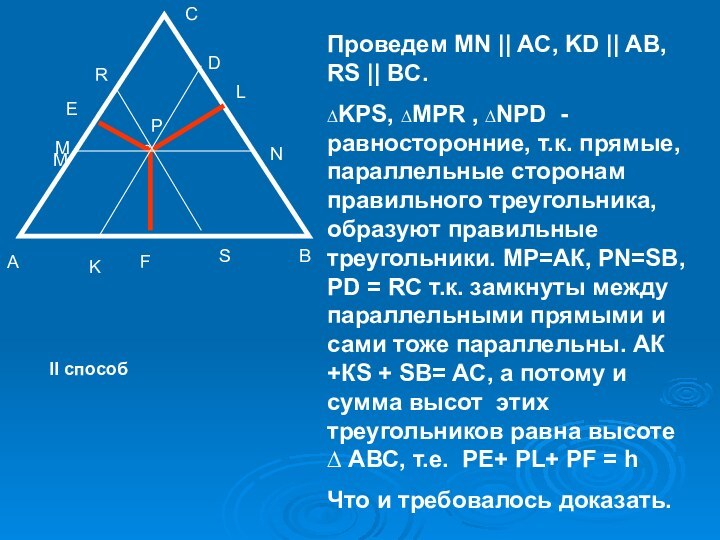
II способ
А
В
С
Е
L
F
P
Дано: ∆ АВС – равносторонний
Доказать: AF + CL + BE = CF + BL + AE
заключение