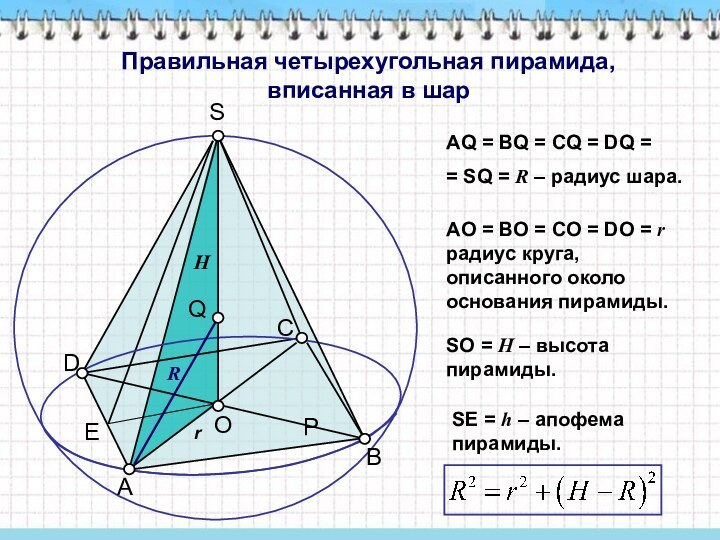
= CQ = SQ= R – радиус шара.
AO =
BO = CO = r – радиус круга, описанного около основания пирамиды.SO = H – высота пирамиды.
SЕ = h – апофема пирамиды.
P
E
T
C
A
B
R
r
H
O
S
Q
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задач на комбинации многогранников и тел вращения
Содержание
- 2. Правильная треугольная пирамида, вписанная в шарАQ =
- 3. Правильная четырехугольная пирамида, вписанная в шарAQ =
- 4. Треугольная пирамида описана около шараE1Q = OQ
- 5. ABCOSDEQE1MPP1Четырехугольная пирамида описана около шараE1Q = P1Q
- 6. Задачи12345Шар вписан в пирамиду. Пирамида вписана в
- 7. В правильную четырехугольную пирамиду вписан шар, объем
- 8. Решение.2) Пусть OQ = x, тогда из
- 9. Площадь поверхности сферы, вписанной в конус, равна
- 10. Решение.2) a – сторона куба, тогда 3)
- 11. Площадь основания конуса равна площади поверхности вписанного
- 12. Ответ:Высота конуса равна 6, а объём равен
- 13. Реши задачу и оформи решение либо на
- 14. Скачать презентацию
- 15. Похожие презентации
Правильная треугольная пирамида, вписанная в шарАQ = ВQ = CQ = SQ= R – радиус шара.AO = BO = CO = r – радиус круга, описанного около основания пирамиды.SO = H – высота пирамиды. SЕ =
Слайд 2
Правильная треугольная пирамида, вписанная в шар
АQ = ВQ
= CQ = SQ= R – радиус шара.
BO = CO = r – радиус круга, описанного около основания пирамиды.
Слайд 3
Правильная четырехугольная пирамида, вписанная в шар
AQ = BQ
= CQ = DQ =
= SQ = R
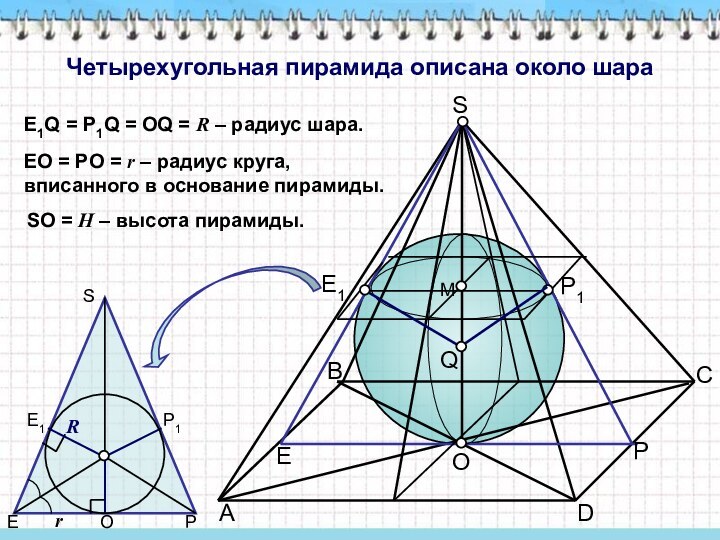
– радиус шара.AO = BO = CO = DO = r радиус круга, описанного около основания пирамиды.
SO = H – высота пирамиды.
SЕ = h – апофема пирамиды.
P
E
D
C
A
B
R
r
H
O
S
Q
Слайд 4
Треугольная пирамида описана около шара
E1Q = OQ =
TQ = R – радиус шара.
EO = PO =
r – радиус круга, вписанного в основание пирамиды.A
B
C
O
S
P
E
Q
E1
T
r
E1
E
O
Q
S
R
R
r
r
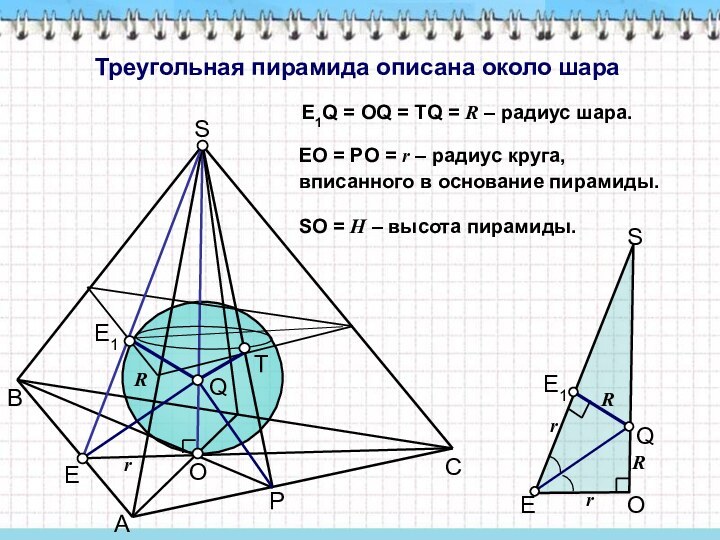
SO = H – высота пирамиды.
R
Слайд 5
A
B
C
O
S
D
E
Q
E1
M
P
P1
Четырехугольная пирамида описана около шара
E1Q = P1Q =
OQ = R – радиус шара.
EO = PO =
r – радиус круга, вписанного в основание пирамиды.SO = H – высота пирамиды.
R
E
P
S
E1
P1
O
r
Слайд 6
Задачи
1
2
3
4
5
Шар вписан в пирамиду.
Пирамида вписана в шар.
Сфера вписана в конус.
Куб вписан в конус.
Шар
вписан в конус.
Слайд 7
В правильную четырехугольную пирамиду вписан шар, объем которого
32π/3. Найдите объем пирамиды, если её высота равна 6.
Решение.
тогда
5)
Тогда сторона основания пирамиды вдвое больше, и равна Ответ: 96.
4
1
Слайд 8
Решение.
2) Пусть OQ = x, тогда из ΔAOQ
выразим сторону АО:
x
3) Составим теорему Пифагора для ΔASO:
Откуда находим
OQ = 4.4) Тогда SO = 5+4=9,
5) В основании пирамиды квадрат, со стороной a, равной
Ответ: 54.
4
3
и АО = 3.
2
Слайд 9
Площадь поверхности сферы, вписанной в конус, равна 100π.
Длина окружности, по которой сфера касается поверхности конуса, равна
6π. Найдите радиус основания конуса.Решение.
A
B
O
S
О1
Р
О2
2) Sсферы = 4πR2 =100π, тогда R = O1P = 5.
3) Из ΔO1O2P по теореме Пифагора находим:
4) В ΔO1PS отрезок РО2 высота, проведенная из вершины прямого угла, значит
5) Найдем высоту конуса SO= SO2 +O2O1+O1O = 2,25 + 4 + 5 = 11,25.
6) Δ SО2Р∞ΔSOВ (∠О2=∠О=90°, ∠S – общий),
откуда
Ответ: 15.
3
4
2,25
15
3
Слайд 10
Решение.
2) a – сторона куба, тогда
3) Выразим
через a:
4) Δ SО1Р1∞ΔSOР (∠О1=∠О=90°, ∠S – общий),
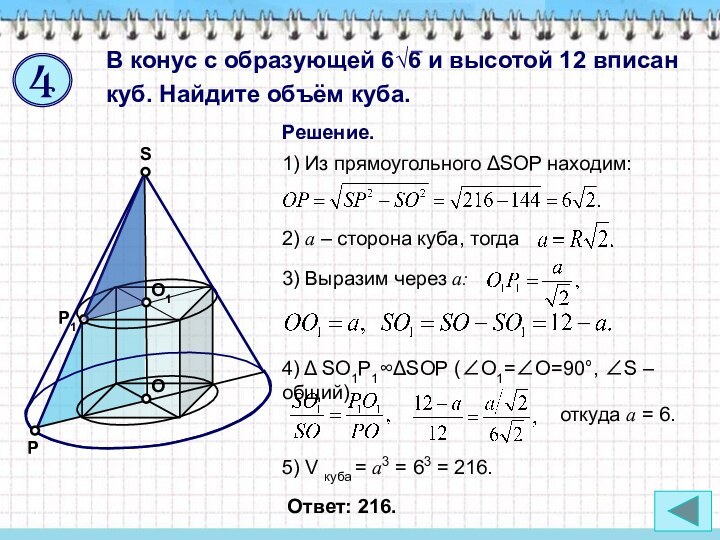
откуда a = 6.
1) Из прямоугольного ΔSOP находим:
5) V куба = a3 = 63 = 216.
Ответ: 216.
4
Слайд 11 Площадь основания конуса равна площади поверхности вписанного в
него шара. Найдите радиус шара, если образующая конуса равна
10.O
S
О1
Р
Р1
Решение.
1) Обозначим радиус шара r, а радиус основания конуса R.
2) По условию
т.е.
3) Δ SP1O1∞ΔSOP (∠Р1=∠О=90°, ∠S – общий),
откуда SO1 = 5 ,
5
5) Тогда
коэффициент подобия треугольников k = ½.
2r
откуда r = 3.
4) Заметим, что РР1= 2r, SP1= 10 – 2r, SO = 5+r.
Ответ: 3.
5
Слайд 12
Ответ:
Высота конуса равна 6, а объём равен 144π.
Найдите площадь полной поверхности куба, вписанного в конус.
Желаю удачи!
Реши самостоятельно
1
2
96
Шар объём которого равен 32π/3, вписан в конус. Найдите высоту конуса, если радиус его основания равен 2√3.
6
Ответ:
Слайд 13 Реши задачу и оформи решение либо на альбомном
листе, либо в виде электронного документа (PowerPoint, Paint, Word
и т.д.)Что нового вы узнали на уроке?
Домашнее задание
Рефлексия
Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?
Чему вы научились?
Какое у вас настроение в конце урока?
