Слайд 2
Содержание проекта
♦ Многогранники
♦ Тела вращения
Слайд 3
Многогранники
Для рассмотрения столь обширной темы
для начала дадим определения многограннику.
Многогранник в (трехмерном пространстве) - геометрическое
тело, ограниченное плоскими многоугольниками.
Эти многоугольники называются гранями, их стороны ребрами, а их вершины - вершинами многогранника.
Рис.1 Октаэдр Рис.2 Тетраэдр Рис.3 Куб Рис.4 Параллелепипед
Слайд 4
Виды многогранников
Правильным многогранником называется такой многогранник, у которого все
грани равны и представляют собой равные правильные многоугольники, все
ребра и все вершины также равны между собой. В то время, как правильных многоугольников существует сколько угодно, правильных многогранников ограниченное число.
Пример: тетраэдр, октаэдр и т.д.
Полуправильные многогранники — в общем случае это различные выпуклые многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.
Слайд 5
Правильные многогранники
В данном разделе мы рассмотрим 5
видов правильных многогранников.
Куб
Тетраэдр
Октаэдр
Икосаэдр
Додекаэдр
Куб — правильный многогранник, каждая грань
которого представляет собой квадрат. Частный
случай параллелепипеда и призмы.
Свойства:
♦ Количество вершин: 8
♦Количество рёбер: 12
♦Количество граней: 6
♦ Граней при вершине: 3
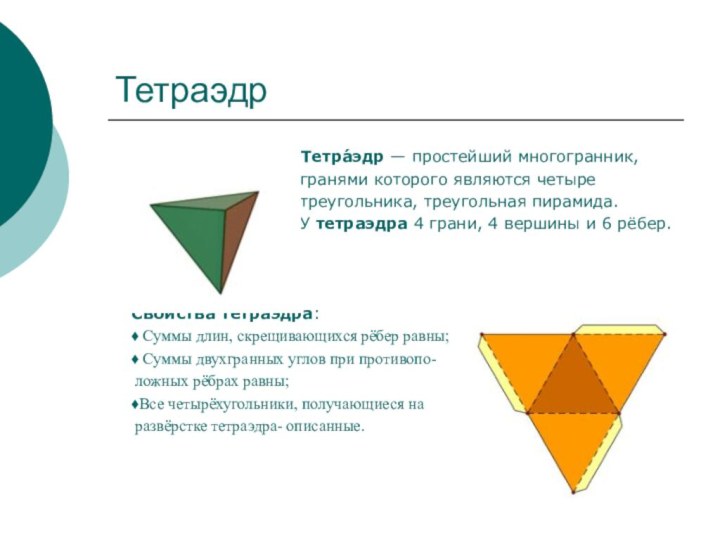
Тетра́эдр — простейший многогранник,
гранями которого являются четыре
треугольника, треугольная пирамида.
У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Свойства тетраэдра:
♦ Суммы длин, скрещивающихся рёбер равны;
♦ Суммы двухгранных углов при противопо-
ложных рёбрах равны;
♦Все четырёхугольники, получающиеся на
развёрстке тетраэдра- описанные.
Слайд 8
Октаэдр
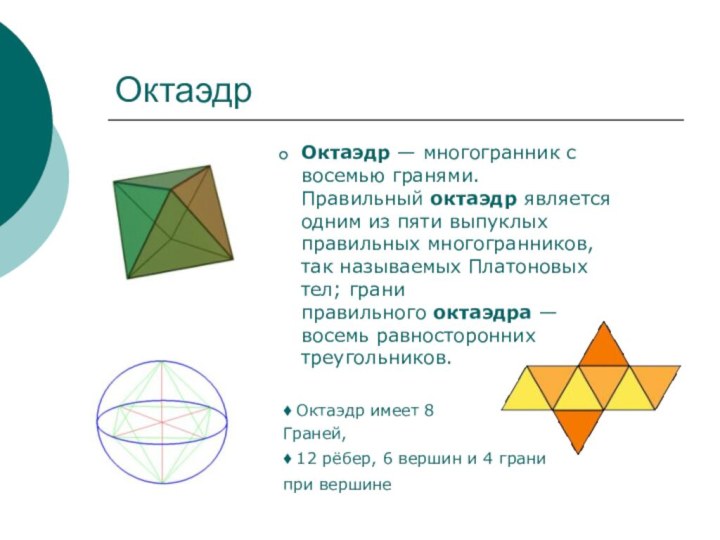
Октаэдр — многогранник с восемью гранями. Правильный октаэдр является одним из
пяти выпуклых правильных многогранников, так называемых Платоновых тел; грани
правильного октаэдра — восемь равносторонних треугольников.
♦ Октаэдр имеет 8
Граней,
♦ 12 рёбер, 6 вершин и 4 грани
при вершине
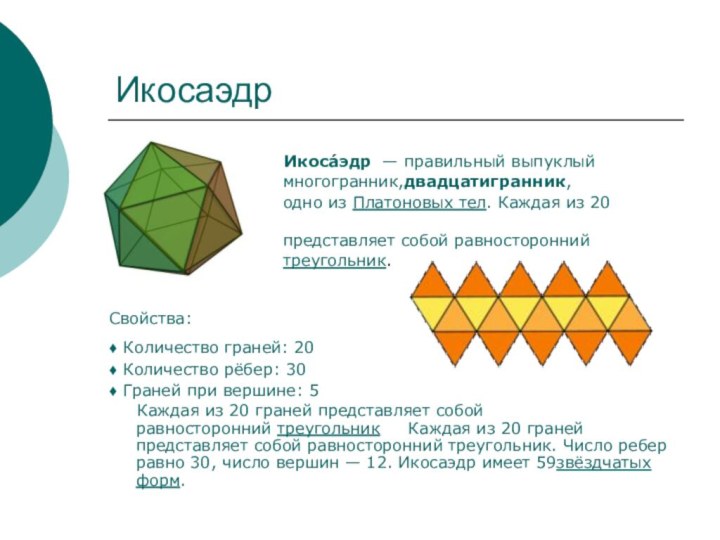
Икоса́эдр — правильный выпуклый
многогранник,двадцатигранник,
одно из Платоновых тел. Каждая из 20 граней
представляет собой равносторонний
треугольник.
Свойства:
♦ Количество граней: 20
♦ Количество рёбер: 30
♦ Граней при вершине: 5
Каждая из 20 граней представляет собой равносторонний треугольник Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59звёздчатых форм.
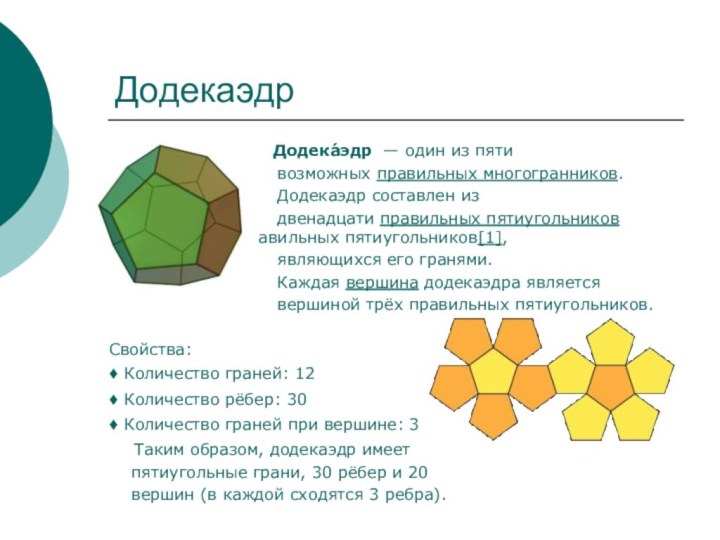
Додека́эдр — один
из пяти
возможных правильных многогранников.
Додекаэдр составлен из
двенадцати правильных пятиугольников двенадцати правильных пятиугольников[1],
являющихся его гранями.
Каждая вершина додекаэдра является
вершиной трёх правильных пятиугольников.
Свойства:
♦ Количество граней: 12
♦ Количество рёбер: 30
♦ Количество граней при вершине: 3
Таким образом, додекаэдр имеет
пятиугольные грани, 30 рёбер и 20
вершин (в каждой сходятся 3 ребра).
Слайд 11
Неправильные многогранники
Неправильные многогранники бывают выпуклыми и невыпуклыми. Выпуклый
многогранник расположен по одну сторону от плоскости каждой своей
грани. Невыпуклый многогранник расположен по разные стороны от одной из плоскости.
Пример выпуклого: куб.
Слайд 12
Невыпуклые многогранники
Однородные многогранники, то есть невыпуклые многогранники, все грани
которых - правильные многоугольники и все многогранные углы которых
равны, действительно существуют. Однородный многогранник может быть невыпуклым в одном из двух случаев.
Пример: пирамида, призма.
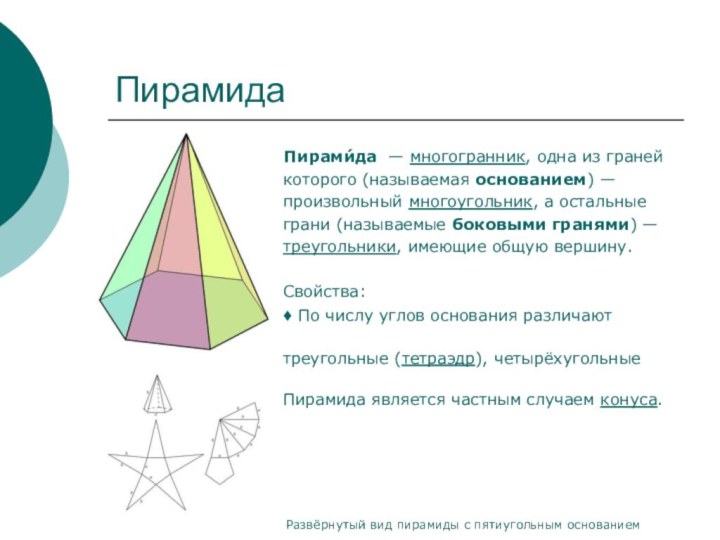
Пирами́да — многогранник,
одна из граней
которого (называемая основанием) —
произвольный многоугольник, а остальные
грани (называемые боковыми гранями) —
треугольники, имеющие общую вершину.
Свойства:
♦ По числу углов основания различают пирамиды
треугольные (тетраэдр), четырёхугольные и т. д.
Пирамида является частным случаем конуса.
Развёрнутый вид пирамиды с пятиугольным основанием
Призма —многогранник, две
грани которого
являются конгруэнтными (равными)
многоугольниками, лежащими в параллельных
плоскостях, а остальные грани —
параллелограммами, имеющими общие стороны
с этими многоугольниками. Эти
параллелограммы называются боковыми
гранями призмы, а оставшиеся два
многоугольника называются её основаниями.
Своства:
♦ Основания призмы являются равными многоугольниками.
♦ Боковые грани призмы являются параллелограммами.
♦ Боковые ребра призмы параллельны и равны
Слайд 15
Тела вращения
Тела вращения — объёмные тела, возникающие при
вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей
в той же плоскости.
Слайд 16
Цилиндр
Цили́ндр — геометрическое тело — геометрическое тело, ограниченное цилиндрической поверхностью — геометрическое тело, ограниченное цилиндрической поверхностью и
двумя параллельными плоскостями,
пересекающими её.
Конус — тело — тело в евклидовом пространстве,
полученное объединением всех лучей, исходящих
из одной точки (вершины конуса) и проходящих
через плоскую поверхность. Иногда конусом
называют часть такого тела, имеющую
ограниченный объём и полученную объединением
всех отрезков, соединяющих вершину и точки плоской
поверхности (последнюю в таком случае
называют основанием конуса, а конус
называют опирающимся на данное основание). Если
основание конуса представляет собой многоугольник,
такой конус является пирамидой.
Шар — геометрическое тело;
совокупность всех точек пространства,
находящихся от центра на расстоянии, не
больше заданного. Это
расстояние называется радиусом шара.
Шар образуется
вращением полукруга вращением полукруга около его неподвижного диаметра вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Сфе́ра — это геометрическое
место точек в пространстве,
равноудаленных от
некоторой заданной точки
(центра сферы).
Сфера является частным случаем эллипсоидаСфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шараСфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объём, также из всех поверхностей с данной площадью сфера ограничивает наибольший объём. Поэтому тела сферической формы встречаются в природе, например, маленькие капли водыСфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объём, также из всех поверхностей с данной площадью сфера ограничивает наибольший объём. Поэтому тела сферической формы встречаются в природе, например, маленькие капли воды при свободном падении приобретают сферическую форму именно из-за минимизации площади поверхности силой поверхностного натяжения.