- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Платоновы и Архимедовы тела (10 класс)
Содержание
- 2. «Предмет математики настолько серьезен, что полезно не упускать случая сделать его немного занимательным» Блез Паскаль
- 3. Содержание:♣ Основные понятия♣ Платоновы тела♣ Архимедовы тела♣ Список используемой литературы
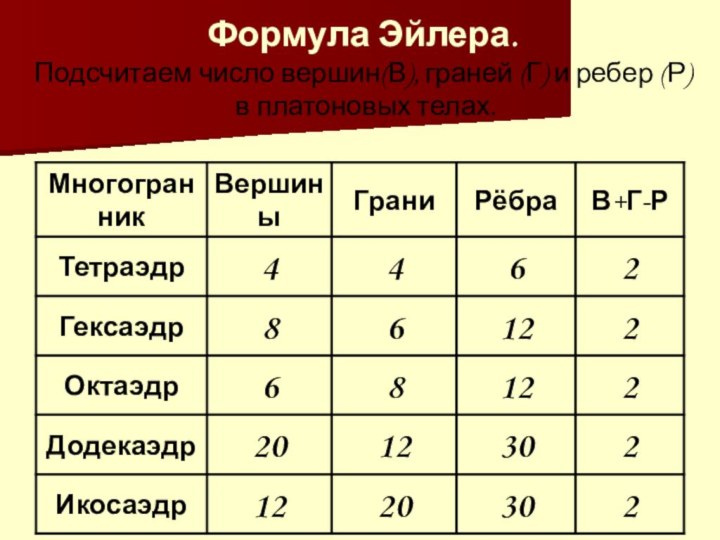
- 4. Основные понятия: Многогранник –
- 5. Платон428 – 347 гг. до н. э.
- 6. В своем диалоге «Тимей» Платон говорит, что
- 7. Многогранник называется правильным, если все его грани
- 8. Все правильные многогранники имеют разное число граней
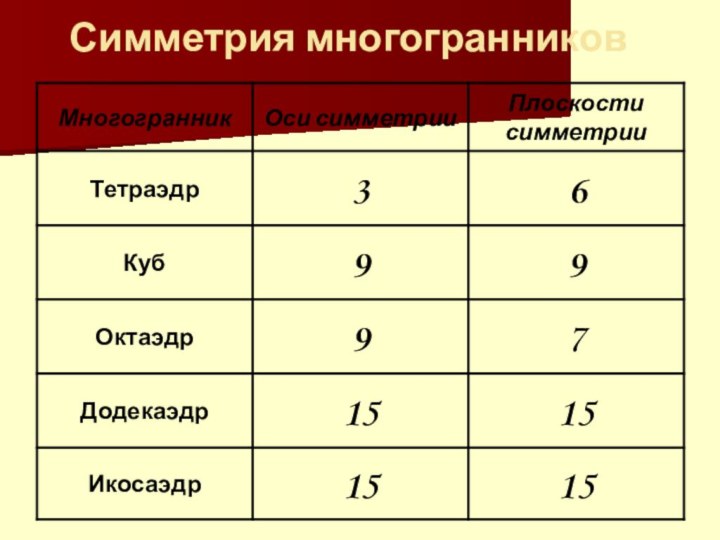
- 9. Формула Эйлера. Подсчитаем число вершин(В), граней (Г) и ребер (Р) в платоновых телах.
- 10. Леонард Эйлер 4(15).4.1707 – 7(18).9.1783
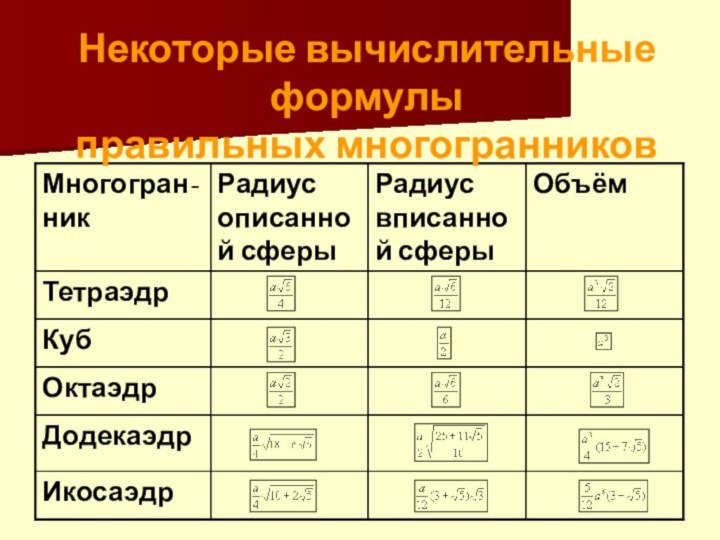
- 11. Симметрия многогранников
- 12. Некоторые вычислительные формулы правильных многогранников
- 13. Свойства Внутри каждого правильного многогранника су-ществует точка,
- 14. „Тайная вечеря“ С. Дали Большой
- 15. Сальвадор Дали «Тайная вечеря»
- 16. Кристаллы Кристаллы — тела, име-ющие многогранную форму. Вот
- 17. Впрочем, многогранники - отнюдь не только объект
- 18. Архимедовы тела Кроме правильных мно-гогранников
- 19. Архимед287 - 212 гг. до н. э.
- 20. Полуправильный многогранник – это… выпуклый многогранник,
- 21. Полуправильные многогранники получаются в процессе усечения вершин правильных многогранников
- 22. Существует 13 видов Архимедовых тел:
- 23. Усеченный тетраэдр Усеченный кубУсеченный тетраэдр – это
- 24. РомбокубооктаэдрРомбокубооктаэдр – это полуправильный многогранник, составленный из
- 25. Усеченный кубооктаэдрКубооктаэдрУсеченный кубооктаэдр – это полу-правильный многогранник,
- 26. Усеченный октаэдрУсеченный додекаэдрУсеченный октаэдр – это полуправильный
- 27. РомбоикосододекаэдрУсеченный икосододекаэдрРомбоикосододекаэдр – это полуправильный многогранник, составленный
- 28. Икосододекаэдр Усеченный икосаэдрИкосододекаэдр – это полуправильный многогранник,
- 29. Плосконосый куб – это полупра-вильный многогранник, составленный
- 30. В основу формирования пространственной конструк-ции положена геометрия
- 31. !!! КОНЕЦ !!!
- 32. Тетраэдр Тетра́эдр — много-гранник с четырьмя
- 33. ГексаэдрГексаэдр (куб, hexa – шесть) – правильный
- 34. Октаэдр Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь»
- 35. Додекаэдр Додека́эдр (от греч. dodeka —
- 36. Скачать презентацию
- 37. Похожие презентации





























Слайд 2 «Предмет математики настолько серьезен, что полезно не упускать
случая сделать его немного занимательным»
Блез Паскаль
Слайд 3
Содержание:
♣ Основные понятия
♣ Платоновы тела
♣ Архимедовы тела
♣ Список
используемой литературы
Слайд 4
Основные понятия:
Многогранник – это
геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми
гранями.Ребра – стороны граней многогранника, а концы ребер – вершины многогранника.
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.
Слайд 6
В своем диалоге «Тимей»
Платон говорит,
что атом
огня имеет
вид тетраэдра,
земли – гексаэдра (куба),
воздуха
– октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра.
Ученики Платона продолжили его дело в
изучении перечисленных тел.
Поэтому эти
многогранники
называют
платоновыми
телами.
Слайд 7
Многогранник называется правильным, если все его грани –
равные между собой правильные многоугольники, из каждой его вершины
выходит одинаковое число ребер и все двугранные углы равны.Что такое правильный
многогранник?
Слайд 8 Все правильные многогранники имеют разное число граней и
названия получили по этому числу. Существует всего пять видов
правильных многогранников:Тетраэдр
Гексаэдр
Октаэдр
Додекаэдр
Икосаэдр
Слайд 13
Свойства
Внутри каждого правильного многогранника су-ществует точка, которая
служит центром трех сфер: описанной сферы (проходящей через все
вершины многогранника); вписанной сферы (касающейся всех его граней); полувписанной сфе-ры (касающаяся всех его ребер).Для каждого правильного многогранника сущест-вует взаимный(двойственный) по отношению к данному многогранник.
Центры граней правильного многогранника слу-жат вершинами взаимного многогранника.
Слайд 14
„Тайная вечеря“ С. Дали
Большой интерес
к формам правильных многогранников проявляли также скульпторы, архитекторы, художники.
Их всех поражало совершенство, гармония многогранников.Леонардо да Винчи (1452 – 1519) увле-кался теорией многогранников и часто изображал их на своих полотнах.
Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.
Слайд 16
Кристаллы
Кристаллы — тела, име-ющие многогранную форму. Вот один
из примеров таких тел: кристалл пирита (сернистый колчедан FeS)
— природная модель додекаэдра.ПИРИТ (от греч. “пир” — огонь) — сернистое железо или серный колчедан. Размеры крис-таллов пирита часто достигают нескольких сантиметров и яв-ляются хорошим коллекционным материалом.
Слайд 17 Впрочем, многогранники - отнюдь не только объект научных
исследований. Их формы — завершенные и при-чудливые, широко используются
в декоративном искусстве.Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.
Ярчайшим примером худо-жественного изображения многогранников в XX веке являются графические фан-тазии Маурица Эшера (1898-1972).
Слайд 18
Архимедовы тела
Кроме правильных мно-гогранников существует
13 полуправильных мно-гогранников, которые носят свое название «тел Архимеда»,
поскольку он первым их описал.Это тела, составленные из многоугольников двух видов, причем в каждой вершине сходится одно и то же число многоугольников каждого вида. Примером такого многогранника является футбольный мяч. Он составлен из пяти шестиугольников.
Слайд 20
Полуправильный многогранник – это…
выпуклый многогранник, обладающий
двумя свойствами:
все его грани являются правильными многоугольниками двух или
более типов (если все грани — правильные много-угольники одного типа, это — правильный многогранник); все многогранные углы при вершинах конгруэнтны.
Слайд 21
Полуправильные многогранники
получаются в процессе усечения вершин правильных многогранников
Слайд 23
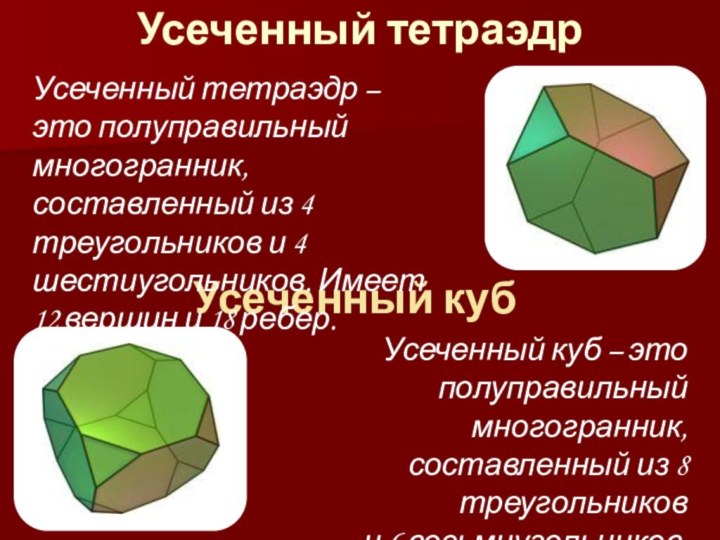
Усеченный тетраэдр
Усеченный куб
Усеченный тетраэдр – это полуправильный многогранник,
составленный из 4 треугольников и 4 шестиугольников. Имеет 12
вершин и 18 ребер.Усеченный куб – это полуправильный многогранник, составленный из 8 треугольников
и 6 восьмиугольников. Имеет 24 вершин и 32 ребра.
Слайд 24
Ромбокубооктаэдр
Ромбокубооктаэдр – это полуправильный многогранник, составленный из 8
треугольников
и 18 квадратов. Имеет 24 вершины и 48 ребра.
Плосконосый
додекаэдрПлосконосый додекаэдр – это полуправильный многогранник, составленный из 80 треугольников и 12 пятиугольников. Имеет 60 вершин и 150 граней.
Слайд 25
Усеченный кубооктаэдр
Кубооктаэдр
Усеченный кубооктаэдр – это полу-правильный многогранник, составлен-ный
из 12 квадратов, 8 шести-угольников и 6 восьмиугольников. Имеет
48 вершин и 72 ребра.Кубооктаэдр – это полупра-вильный многогранник , составленный из 8 треугольников
и 6 квадратов. Имеет 12 вершин и 24 ребра.
Слайд 26
Усеченный октаэдр
Усеченный додекаэдр
Усеченный октаэдр – это полуправильный многогранник,
составленный их 6 квадратов и 8 шестиугольников. Имеет 24
вершины и 36 ребер.Усеченный додекаэдр – это полуправильный многогранник, составленный из 20 треугольников
12 десятиугольников. Имеет 60 вершины и 90ребер.
Слайд 27
Ромбоикосододекаэдр
Усеченный икосододекаэдр
Ромбоикосододекаэдр – это полуправильный многогранник, составленный из
20 треугольников, 30 квадратов и 12 пятиугольников. Имеет 60
вершин и 120 ребер.Усеченный икосододекаэдр – это полуправильный многогранник, состав-ленный из 30 квадратов, 20 шести-угольников и 12 десятиугольников. Имеет 120 вершин и 180 ребер.
Слайд 28
Икосододекаэдр
Усеченный икосаэдр
Икосододекаэдр – это полуправильный многогранник,
составленный из
20 треугольников и 12 пятиугольников. Имеет 30 вершин и
60 ребер.Усеченный икосаэдр – это полуправильный многогранник, составленный из 12 пятиугольников и 20 шестиугольников. Имеет 60 вершин и 90 ребер.
Слайд 29 Плосконосый куб – это полупра-вильный многогранник, составленный из
32 треугольников и 6 квадратов. Имеет 24 вершины и
60 ребер.Плосконосый куб
Слайд 30 В основу формирования пространственной конструк-ции положена геометрия Платона
и Архимеда, позво-ляющая создавать практичес-ки любые ком-
позиционные
решения из
правильных
и полупра-
вильных
многогран-
ников.
Слайд 32
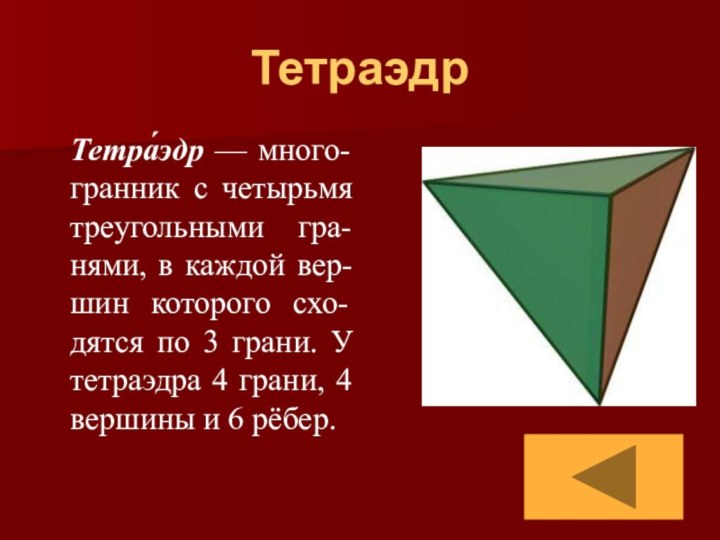
Тетраэдр
Тетра́эдр — много-гранник с четырьмя треугольными
гра-нями, в каждой вер-шин которого схо-дятся по 3 грани.
У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Слайд 33
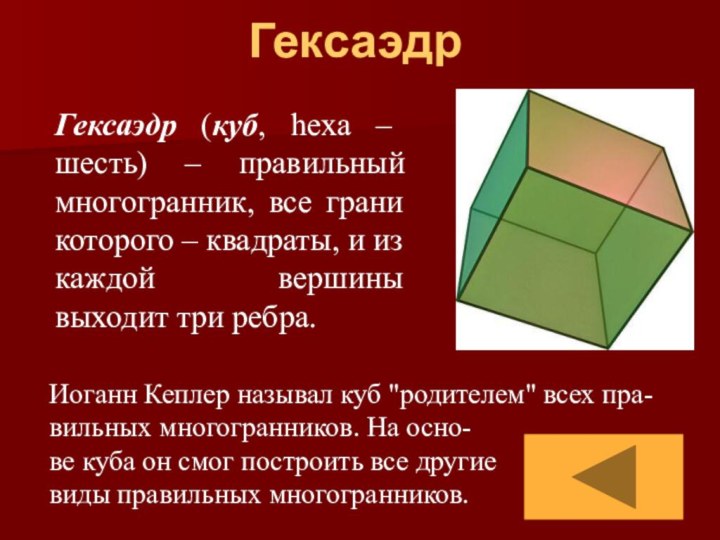
Гексаэдр
Гексаэдр (куб, hexa – шесть) – правильный многогранник,
все грани которого – квадраты, и из каждой вершины
выходит три ребра.Иоганн Кеплер называл куб "родителем" всех пра-вильных многогранников. На осно-
ве куба он смог построить все другие
виды правильных многогранников.
Слайд 34
Октаэдр
Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и
греч. έδρα - «основание») — один из пяти правильных
многогранников, имеющий 8 граней (треугольных), 12 рёбер, 6 вершин (в каждой вершине сходятся 4 ребра).
Слайд 35
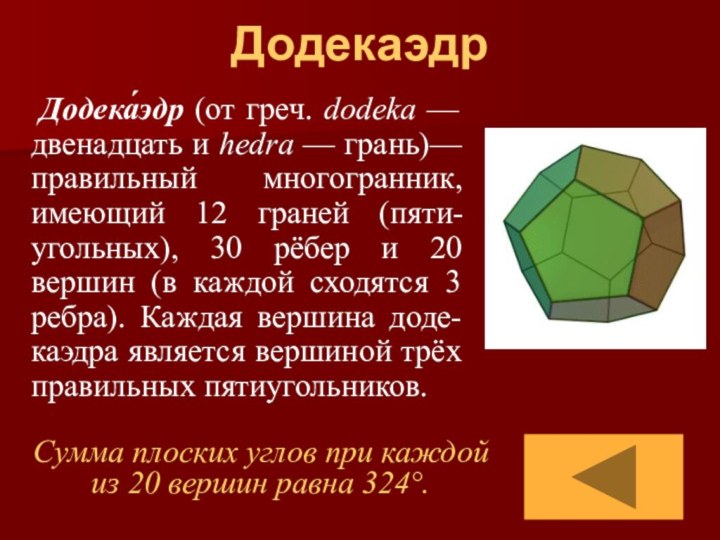
Додекаэдр
Додека́эдр (от греч. dodeka — двенадцать
и hedra — грань)— правильный многогранник, имеющий 12 граней
(пяти-угольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Каждая вершина доде-каэдра является вершиной трёх правильных пятиугольников.Сумма плоских углов при каждой из 20 вершин равна 324°.