- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Центральные и вписанные углы
Содержание
- 2. Центральный угол Центральный угол — угол с вершиной в центре окружности. Центральный угол равен радианной/градусной мере дуги, на которую опирается.
- 3. ПримерТочка О – центр окружности, угол АСВ=65°.
- 4. ЗадачаТочка О – центр окружности, угол АСВ=70°. Найдите величину угла АОВ.Решение
- 5. ЗадачаТочка О – центр окружности, угол АСВ=70°.
- 6. ЗадачаТочка О – центр окружности, угол АСВ=25°. Найдите величину угла АОВ.Решение
- 7. ЗадачаТочка О – центр окружности, угол АСВ=25°.
- 8. ЗадачаТочка О – центр окружности, угол АСВ=65°. Найдите величину угла АОВ.Решение
- 9. ЗадачаТочка О – центр окружности, угол АСВ=65°.
- 10. ЗадачаТочка О – центр окружности, угол АСВ=79°. Найдите величину угла АОВ.Решение
- 11. ЗадачаТочка О – центр окружности, угол АСВ=79°.
- 12. ЗадачаТочка О – центр окружности, угол АСВ=43°. Найдите величину угла АОВ.Решение
- 13. ЗадачаТочка О – центр окружности, угол АСВ=43°.
- 14. Вписанный уголВписанный угол — угол, вершина которого лежит на окружности,
- 15. ПримерНайдите вписанный угол, опирающийся на дугу, которая
- 16. Задача Найти величину угла А0С (см. рис.), если угол АВС равен Решение
- 17. ЗадачаНайти величину угла А0С (см. рис.), если
- 18. ЗадачаНайти величину угла ВАD, изображенного на картинке:Решение
- 19. ЗадачаНайти величину угла ВАD, изображенного на картинке:Так
- 20. Найти величину угла D, изображенного на картинке:ЗадачаРешение
- 21. Задача Найти величину угла D, изображенного на
- 22. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.ЗадачаРешение
- 23. ЗадачаЦентральный угол на больше острого вписанного угла, опирающегося
- 24. Найти градусную меру угла ВАD:Задача Решение
- 25. Задача Найти градусную меру угла ВАD:
- 26. Хо́рдаХо́рда— отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы).
- 27. ПримерНайдите хорду, на которую опирается угол 30˚,
- 28. ЗадачаХорда AB делит окружность на две части, градусные величины
- 29. Так как дуги ACB, AB относятся друг другу
- 30. Найти длину отрезка ME:ЗадачаРешение
- 31. ЗадачаНайти длину отрезка ME:По свойству пересекающихся хорд ME*EP = NE *EQ3*4 = ME*6Ответ: 2.
- 32. ЗадачаХорда AB стягивает дугу окружности в 82˚. Найдите угол ABC между
- 33. Проведем радиус в точку касания . По свойству
- 34. Касательная к окружностиПрямая, имеющая одну общую точку
- 35. ПримерЧерез концы A и B дуги окружности в 620 проведены касательные AC иBC. Найдите
- 36. ЗадачаНайдите угол ACO, если его сторона CA касается окружности, O — центр
- 37. ЗадачаНайдите угол ACO, если его сторона CA касается окружности, O — центр
- 38. ЗадачаНайдите угол ACO, если его сторона CA касается окружности, O — центр
- 39. Центральный угол AOD, как опирающийся на дугу AD, равен
- 40. ЗадачаК окружности с центром в точке О
- 41. По свойству касательной и секущей, проведенных из
- 42. Дополнительные Свойства, используемые для решения задач.
- 43. Свойство первоеa=1/2( AB+ CD)Угол, вершина
- 44. Свойство второеa=1/2( AB- CD)Угол, вершина
- 45. Свойство третьеa=1/2 ACУгол, составленный касательной и хордой, измеряется половиной дуги, заключенной внутри его.
- 46. Свойство четвертоеa =AD*n
- 47. Теорема о касательной и секущей
- 48. Теорема перваяВеличина угла, образованного касательной и хордой,
- 49. На рисунке, где MA - касательная, а
- 50. Скачать презентацию
- 51. Похожие презентации







































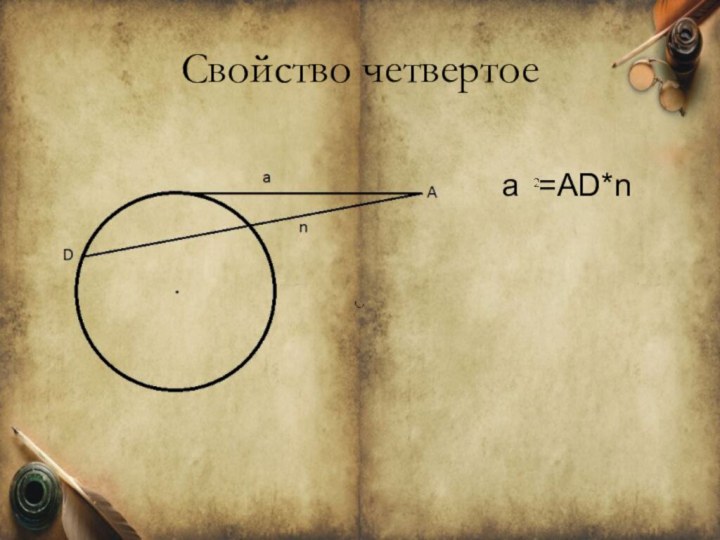



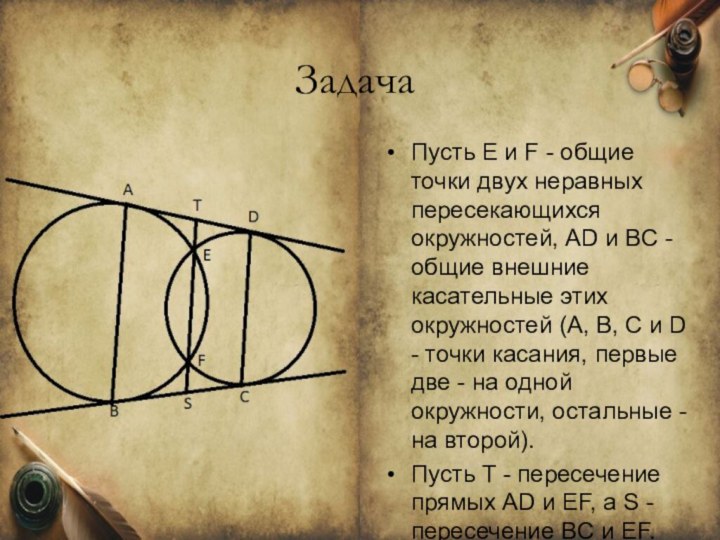
Слайд 2
Центральный угол
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен
радианной/градусной мере дуги, на которую опирается.
Слайд 3
Пример
Точка О – центр окружности, угол АСВ=65°. Найдите
величину угла АОВ.
Так как, вписанный угол равен половине центрального,
опирающегося на ту же дугу, тоАСВ=1/2АОВ
1/2АОВ=65°
АОВ=130°
Слайд 5
Задача
Точка О – центр окружности, угол АСВ=70°. Найдите
величину угла АОВ.
Так как, вписанный угол равен половине центрального,
опирающегося на ту же дугу, тоАСВ=1/2АОВ
1/2АОВ=70°
АОВ=140°
Слайд 7
Задача
Точка О – центр окружности, угол АСВ=25°. Найдите
величину угла АОВ.
Так как, вписанный угол равен половине центрального,
опирающегося на ту же дугу, тоАСВ=1/2АОВ
1/2АОВ=25°
АОВ=50°
Слайд 9
Задача
Точка О – центр окружности, угол АСВ=65°. Найдите
величину угла АОВ.
Так как, вписанный угол равен половине центрального,
опирающегося на ту же дугу, тоАСВ=1/2АОВ
1/2АОВ=65°
АОВ=130°
Слайд 11
Задача
Точка О – центр окружности, угол АСВ=79°. Найдите
величину угла АОВ.
Так как, вписанный угол равен половине центрального,
опирающегося на ту же дугу, тоАСВ=1/2АОВ
1/2АОВ=79°
АОВ=158°
Слайд 13
Задача
Точка О – центр окружности, угол АСВ=43°. Найдите
величину угла АОВ.
Так как, вписанный угол равен половине центрального,
опирающегося на ту же дугу, тоАСВ=1/2АОВ
1/2АОВ=43°
АОВ=86°
Слайд 14
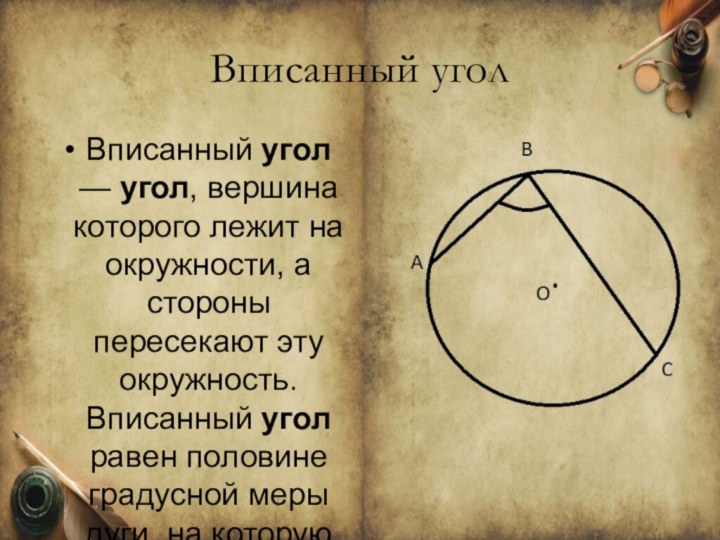
Вписанный угол
Вписанный угол — угол, вершина которого лежит на окружности, а
стороны пересекают эту окружность. Вписанный угол равен половине градусной меры
дуги, на которую опирается.
Слайд 15
Пример
Найдите вписанный угол, опирающийся на дугу, которая составляет окружности.
Окружность
составляет 360° , поэтому дуга АС, которая составляет 4/9 окружности, равняется
4/9*360°=160° . Поэтому вписанный угол АВС равен 80° , так как градусная мера вписанного угла вдвое меньше градусной меры дуги, на которую опирается.Ответ: 80°
Слайд 17
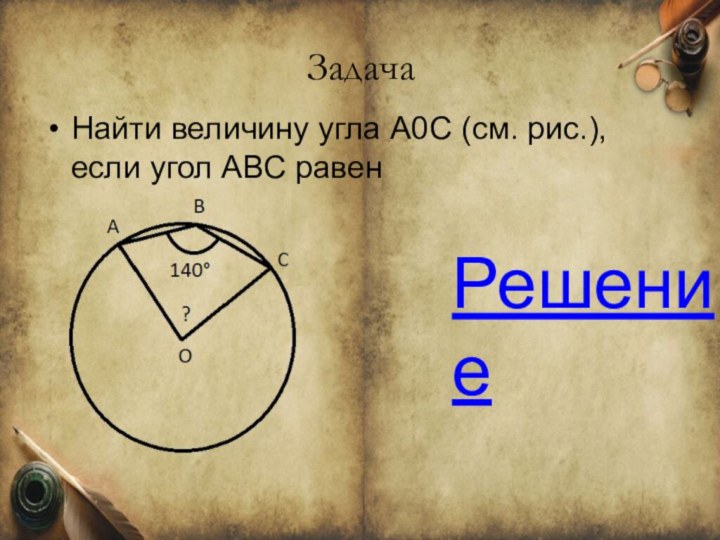
Задача
Найти величину угла А0С (см. рис.), если угол
АВС равен
Заметим, тот угол АОС, что помечен на картинке,
хоть и является центральным углом, но не является соответствующим для вписанного угла АВС, так как они опираются на разные дуги (угол АВС опирается на дугу АС, а угол АОС — на дугу АВС).Так как вписанный угол АВС, равный 140°, опирается на дугу АС, то она равна 280° . Значит дуга АВС равна 360°-280°=80° . А значит центральный угол АОС, который измеряется градусной мерой дуги, на которую опирается, равен 80°.
Слайд 19
Задача
Найти величину угла ВАD, изображенного на картинке:
Так как
углы ВСА и ВDA опираются на одну дугу (АВ),
то они равны, то есть .BDA=40°
Теперь обратимся к треугольнику АВD. Он прямоугольный, так как угол АВD, опирающийся на диаметр, — прямой. Значит, BAD=90°-40°=50°.
Слайд 21
Задача
Найти величину угла D, изображенного на картинке:
ASB=
CSD=110° как вертикальные.
Из треугольника АВS:
BAS=180°-110°-40°=30°BAS= BDC=30°, так как
Углы опираются на одну
дугу.
Слайд 22 Центральный угол на больше острого вписанного угла, опирающегося на
ту же дугу окружности. Найдите вписанный угол.
Задача
Решение
Слайд 23
Задача
Центральный угол на больше острого вписанного угла, опирающегося на
ту же дугу окружности. Найдите вписанный угол.
Обозначим градусную меру
угла АСВ за x, тогда AOD = x+20°Так как центральный угол вдвое больше соответствующего вписанного угла, то составим уравнение: 2x=x+20 , откуда
x = 20°
Слайд 25
Задача
Найти градусную меру угла ВАD:
CDA=50°,
следовательно ABC=100° как дуга вписанного угла. Аналогично, CKB=20°,
следовательноBC=40°. Тогда AB=ABC-BC=60°. А так как AD=180° (AD — диаметр), то BCD=180° -60°= =120° . А значит, BAD=60°.
Слайд 26
Хо́рда
Хо́рда— отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы).
Слайд 27
Пример
Найдите хорду, на которую опирается угол 30˚, вписанный
в окружность радиуса 43.
Угол AOC – соответствующий центральный для вписанного
угла в 30°.Значит, по свойству вписанных углов, AOC=60°.
Тогда треугольник AOC – не просто равнобедренный, но и равносторонний A= C=(180°-60°)/2.
А значит, AC=AO=OC=43
Слайд 28
Задача
Хорда AB делит окружность на две части, градусные величины которых
относятся как 11:61. Под каким углом видна эта хорда
из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.Решение
Слайд 29 Так как дуги ACB, AB относятся друг другу как
11:61, то пусть дуга ACB=11x градусов, а дуга AB=61x градусов.
Тогда, поскольку вся окружность составляет 360° , то11x+61x=360
72x=360
X=5
Тогда на большую дугу AB приходится 61*5°=305°.
А угол ABC, что мы ищем – вписанный, опирающийся на дугу AB , равную 305˚. Значит он равен половине ее градусной меры, то есть 152,5°
Ответ: 152,5.
Хорда AB делит окружность на две части, градусные величины которых относятся как 11:61. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Задача
Слайд 31
Задача
Найти длину отрезка ME:
По свойству пересекающихся хорд ME*EP
= NE *EQ
3*4 = ME*6
Ответ: 2.
Слайд 32
Задача
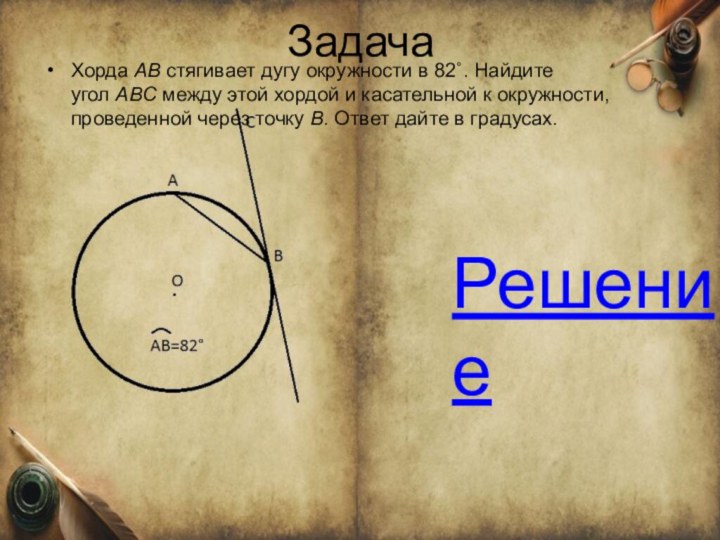
Хорда AB стягивает дугу окружности в 82˚. Найдите угол ABC между этой
хордой и касательной к окружности, проведенной через точку B. Ответ
дайте в градусах.Решение
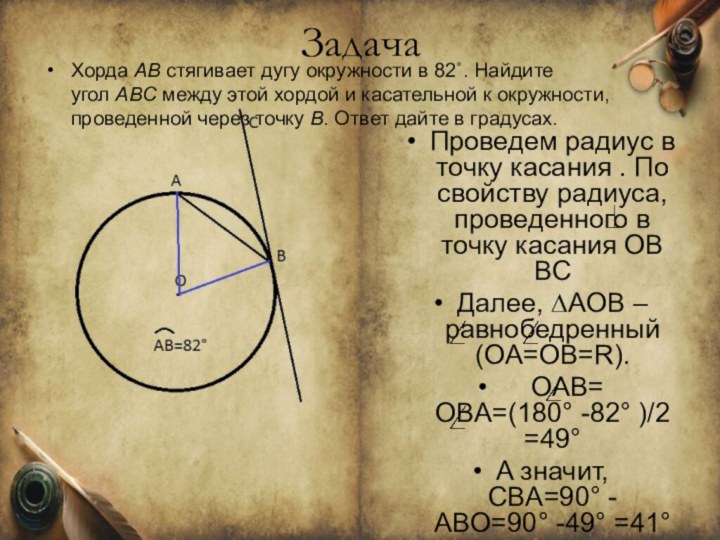
Слайд 33 Проведем радиус в точку касания . По свойству радиуса,
проведенного в точку касания OB BC
Далее, ∆AOB –
равнобедренный (OA=OB=R). OАB= OBA=(180° -82° )/2=49°
A значит, CBA=90° - ABO=90° -49° =41°
Ответ: 41° .
Задача
Хорда AB стягивает дугу окружности в 82˚. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Слайд 34
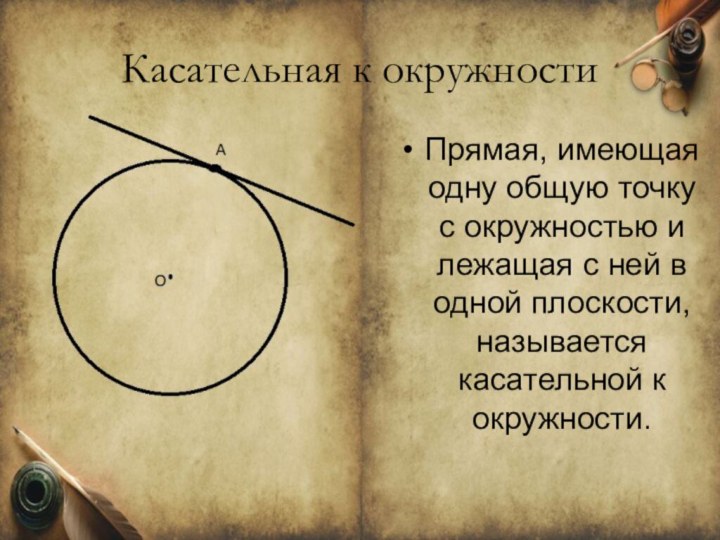
Касательная к окружности
Прямая, имеющая одну общую точку с окружностью и
лежащая с ней в одной плоскости, называется касательной к
окружности.
Слайд 35
Пример
Через концы A и B дуги окружности в 620 проведены касательные AC иBC. Найдите угол ACB.
Ответ дайте в градусах.
Так как ВС и АС касательные,
то по свойству касательной:OBC= OAC=900
Известно, что сумма углов в четырёхугольнике равна 3600.
В четырёхугольнике ОАСВ нам известны три угла, можем найти четвёртый:
OBC+ OAC+ ACB+ AOB=3600
900 + 900 + ACB +620 =3600
ACB = 1180
Слайд 36
Задача
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности,
а меньшая дуга окружности AB, заключенная внутри этого угла, равна
67˚. Ответ дайте в градусах.Решение
Слайд 37
Задача
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности,
а меньшая дуга окружности AB, заключенная внутри этого угла, равна
67˚. Ответ дайте в градусах.Раз дуга AB, заключенная внутри угла C, равна 67˚, то центральный угол AOB, на нее опирающийся, равен также 67˚.
А поскольку OAC=90˚ (радиус, проведенный в точку касания, перпендикулярен касательной), то в треугольнике ACO нам известны два угла.
ACO=180 ˚-90 ˚-67 ˚=23 ˚
Слайд 38
Задача
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности,
а большая дуга AD окружности, заключенная внутри этого угла, равна 136˚.
Ответ дайте в градусах.Решение
Слайд 39
Центральный угол AOD, как опирающийся на дугу AD, равен 136˚.
Тогда
смежный ему угол AOB равен 44˚.
Далее задача аналогична предыдущей.
C
= 180˚-90˚-44˚=46˚Задача
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 136˚. Ответ дайте в градусах.
Слайд 40
Задача
К окружности с центром в точке О проведены
касательная AB и секущая АО. Найдите радиус окружности, если
AB=15, АО=17.Решение
Слайд 41 По свойству касательной и секущей, проведенных из одной
точки к окружности
AB =AC*AD
15 =(17-R)(17+R), где R=OC=OD
R
=17 -15 R =(17-15)(17+15)
R =64
R=8
Ответ:8
К окружности с центром в точке О проведены касательная AB и секущая АО. Найдите радиус окружности, если AB=15, АО=17.
Задача
Слайд 43
Свойство первое
a=1/2( AB+ CD)
Угол, вершина которого
лежит внутри круга, измеряется полусуммой двух дуг, одна из
которых заключена между его сторонами, а другая – между продолжениями сторон.
Слайд 44
Свойство второе
a=1/2( AB- CD)
Угол, вершина которого
лежит вне круга, измеряется полуразностью двух дуг, заключенных между
его сторонами.
Слайд 45
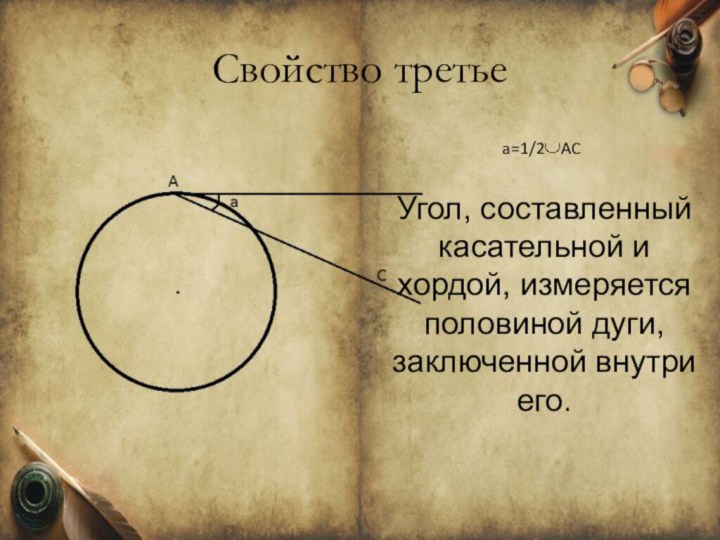
Свойство третье
a=1/2 AC
Угол, составленный касательной и хордой,
измеряется половиной дуги, заключенной внутри его.
Слайд 48
Теорема первая
Величина угла, образованного касательной и хордой, имеющими
общую точку на окружности, равна половине угловой величины дуги,
заключенной между его сторонами.Доказательство
Рассмотрим угол NАВ, образованный касательной NA и хордой AB.
Проведем диаметр АС. Касательная перпендикулярна диаметру, проведенному в точке касания, следовательно, угол(CAN)=90°
Известно, что вписанный угол равен половине центрального угла дуги, на которую он опирается. Отсюда имеем, что угол(BAC) равен половине угловой величины дуги ВС или половине угла(ВОС). угол(BAC)=угол(BOC)/2.
угол(NAB)=90°-угол(BAC), отсюда получаем
угол(NAB)=90°-угол(BOC)/2=(180°-угол(BOC))/2=угол(АОВ)/2
то есть равен половине угловой величины дуги ВА.
Фактически, это вырожденный случай теоремы о величине вписанного угла, когда вершина угла достигает конца дуги (хорды). Одна из сторон угла при этом становится касательной.
Слайд 49 На рисунке, где MA - касательная, а MCB
- секущая, эта теорема выглядит так: МА2=МВ*МС. Докажем это.По
предыдущей теореме угол МАС равен половине угловой величины дуги АС. Но вписанный угол ABC тоже опирается на дугу AC, и по теореме о величине вписанного угла равен половине угловой величины дуги АС. Оба угла равны половине угловой величины дуги AC, следовательно, эти углы равны между собой. угол(MAC)= угол(ABC). Принимая во внимание то, что у треугольников АМС и ВМА угол при вершине М общий, констатируем подобие этих треугольников по двум углам. Из подобия имеем: MC/MA=МА/MB, откуда получаем МА2=МВ*МСТеорема вторая
Если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.