- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему урока геометрии по теме Соотношения между сторонами и углами прямоугольного треугольника
Содержание
- 2. Приветствую вас на уроке геометрии в 8 классе Уроки №59-6006.02.2017 г.
- 3. Успешного усвоения материала Интересные мысли и высказывания Геометрия приближает разум к истинеПлатон
- 4. Отчёт по выполнению ДР в группе
- 5. КР№4 – 16 февраля.
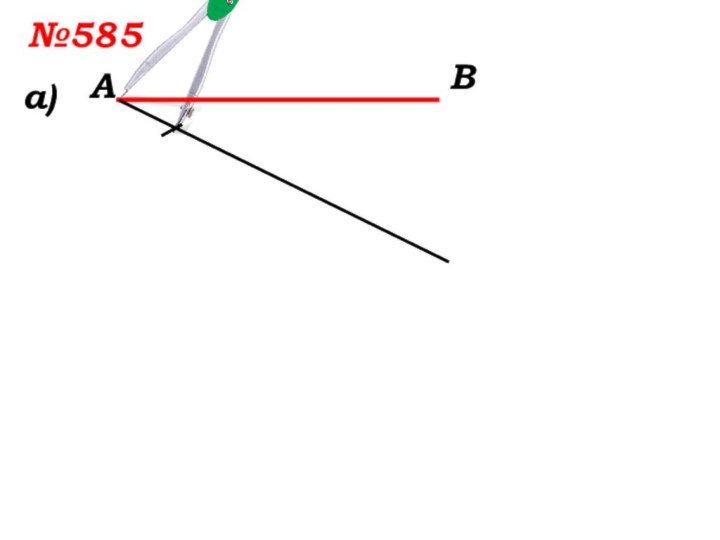
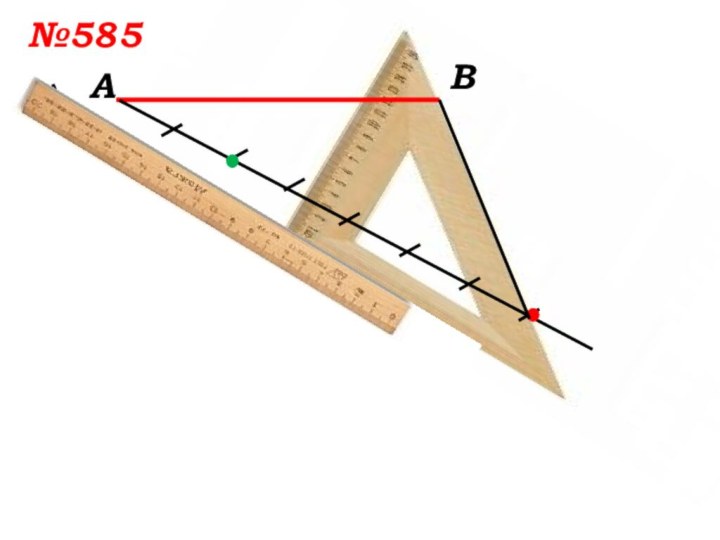
- 6. №585 а)АВ
- 7. №585 а)АВ
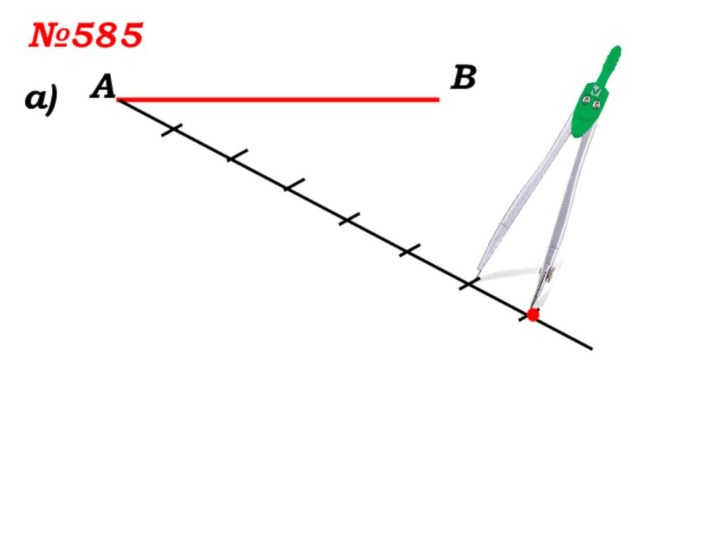
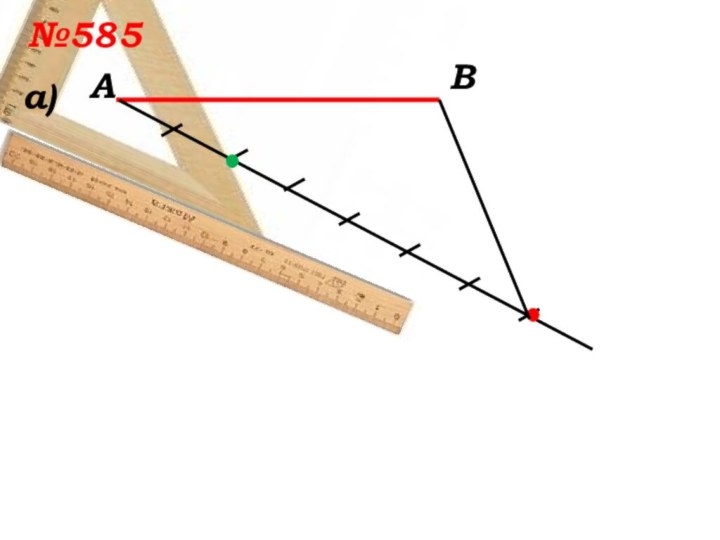
- 8. №585 а)АВ
- 9. №585 а)АВ
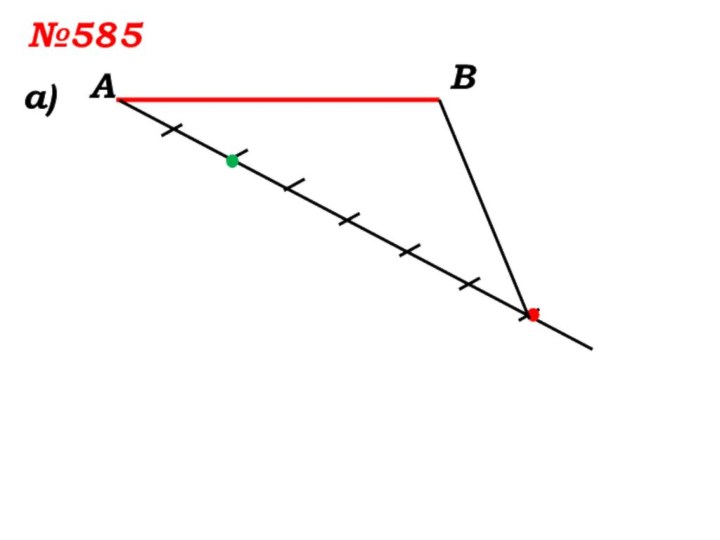
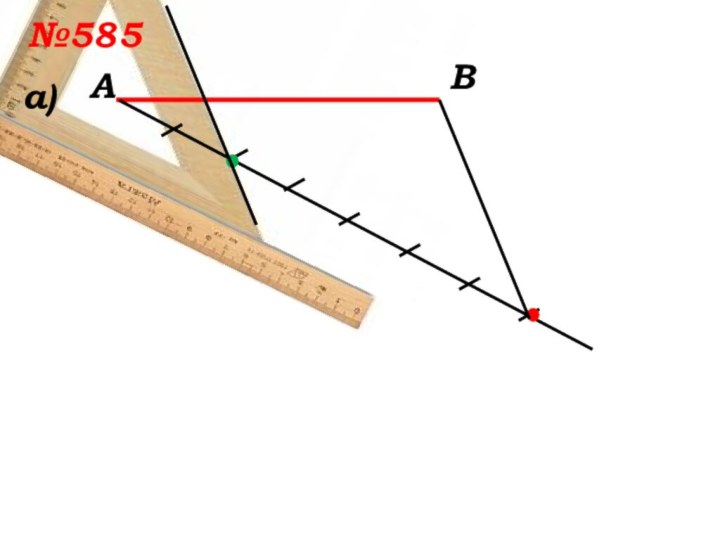
- 10. №585 а)АВ
- 11. №585 а)АВ
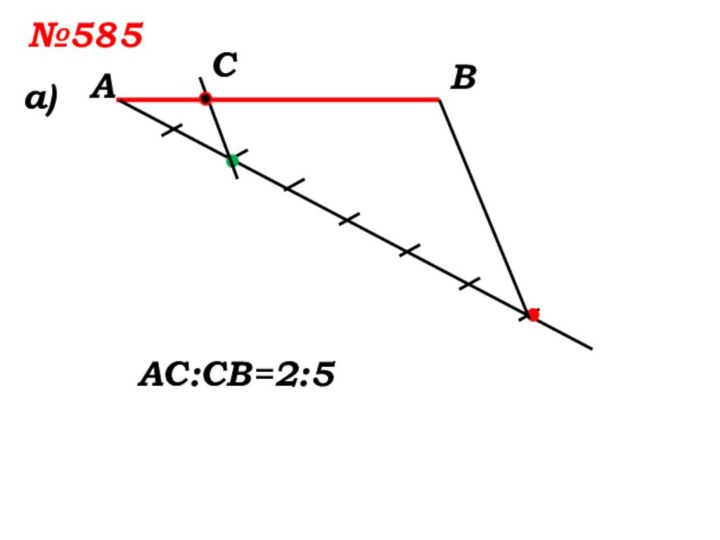
- 12. №585 а)АВСАС:СВ=2:5
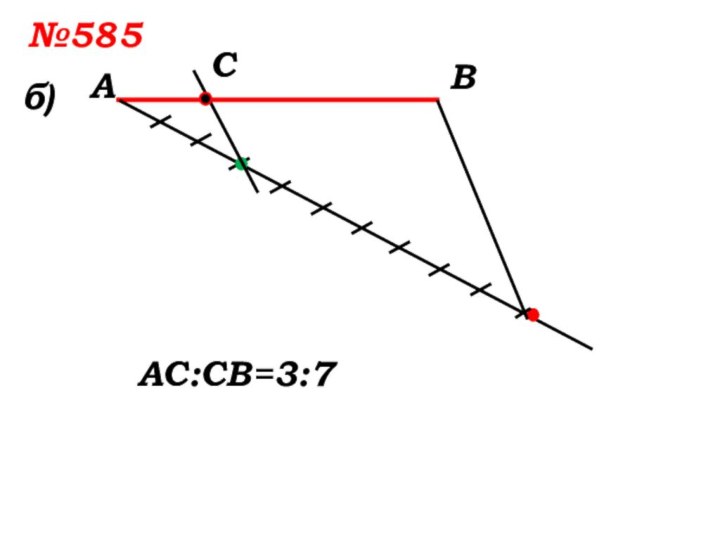
- 13. №585 б)АВСАС:СВ=3:7
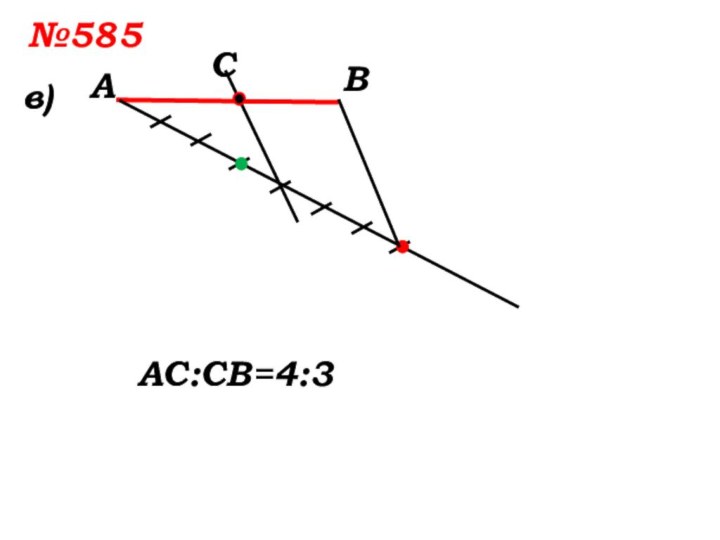
- 14. №585 в)АВСАС:СВ=4:3
- 15. Оцените ДР
- 16. КРСоотношения между сторонами и углами прямоугольного треугольника§4, п.6606.02.2017г.
- 17. Ввести понятие синуса, косинуса и тангенса острого
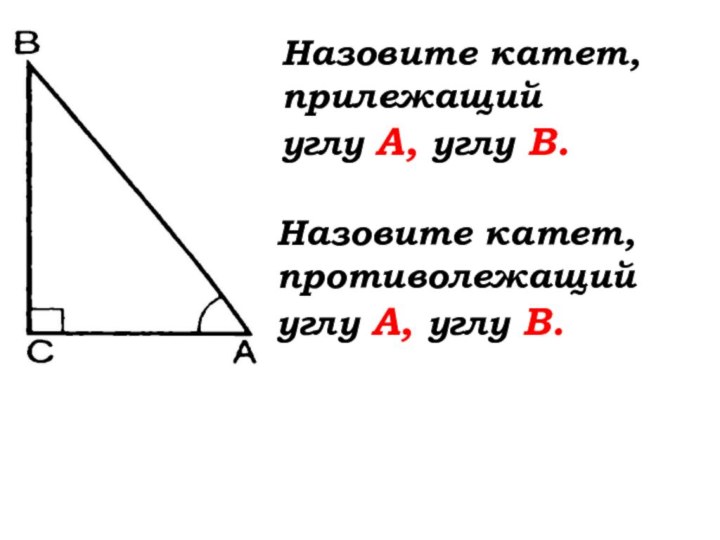
- 18. Назовите катет, прилежащий углу А, углу В.Назовите катет, противолежащий углу А, углу В.
- 19. Стр.156, п.66 Прочитайте определение синуса острого
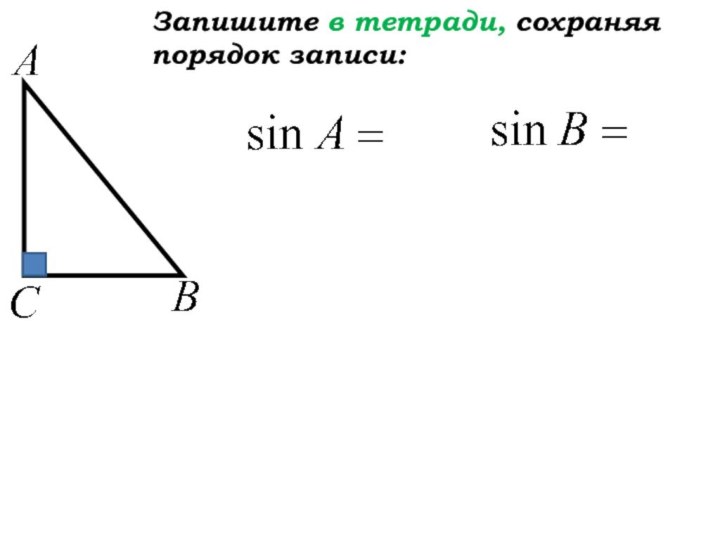
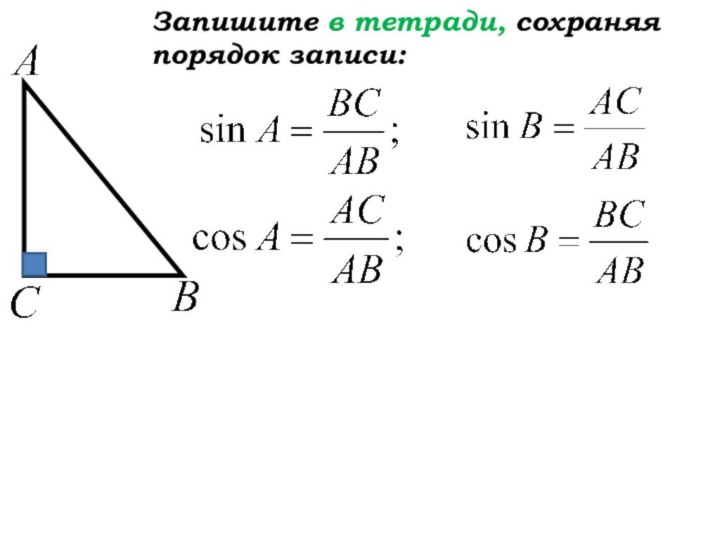
- 20. Запишите в тетради, сохраняя порядок записи:
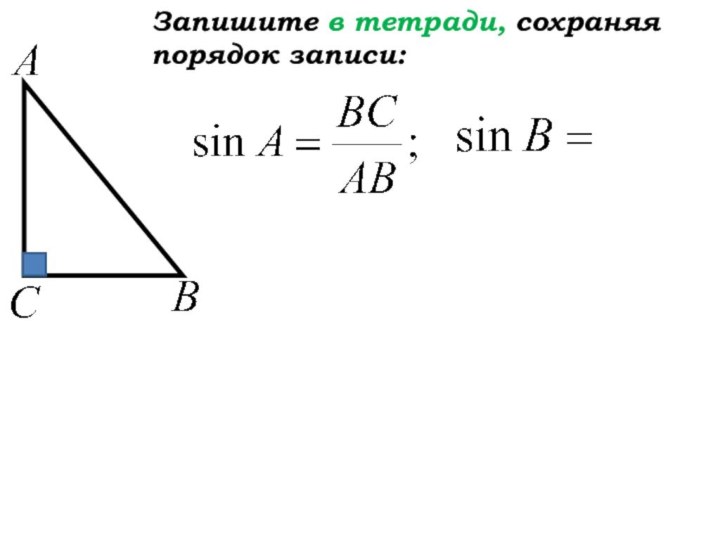
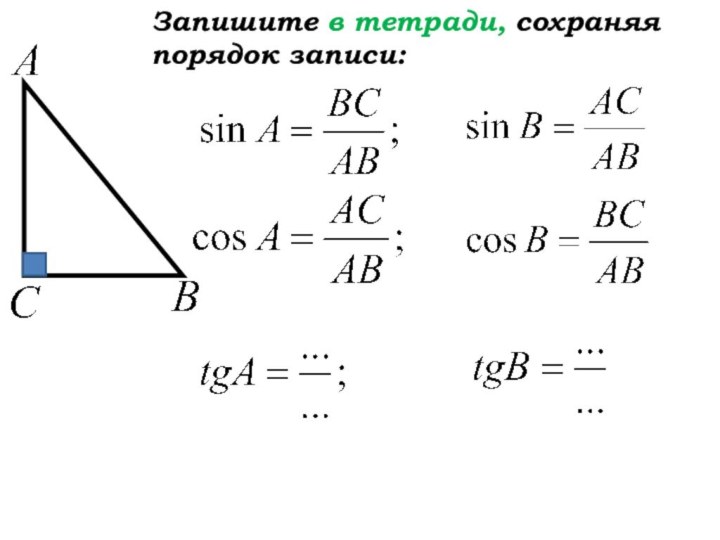
- 21. Запишите в тетради, сохраняя порядок записи:
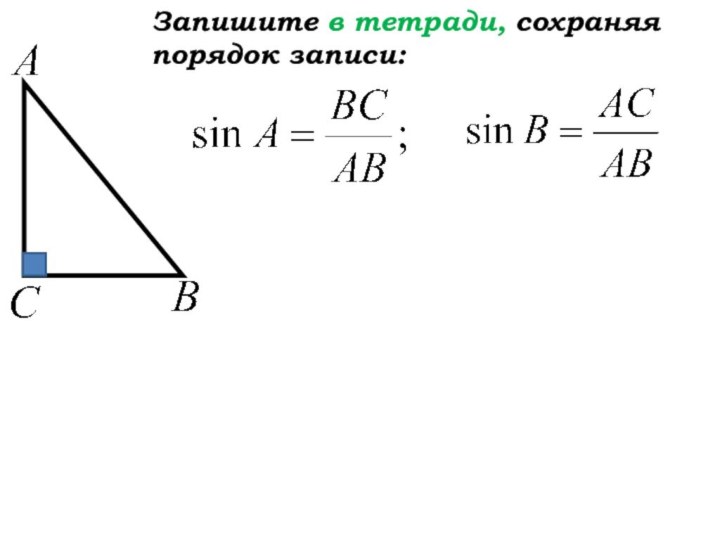
- 22. Запишите в тетради, сохраняя порядок записи:
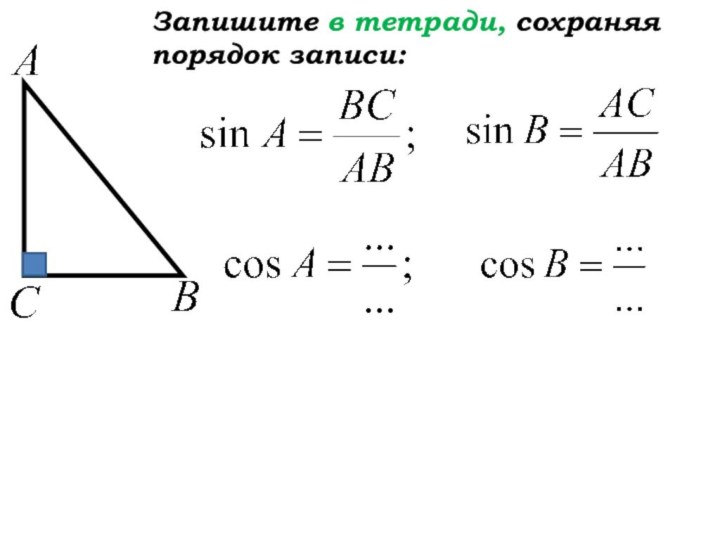
- 23. Стр.156, п.66 Прочитайте определение косинуса острого
- 24. Запишите в тетради, сохраняя порядок записи:
- 25. Запишите в тетради, сохраняя порядок записи:
- 26. Стр.156, п.66 Прочитайте определение тангенса острого
- 27. Запишите в тетради, сохраняя порядок записи:
- 28. Дайте определение синуса, косинуса, тангенса !!
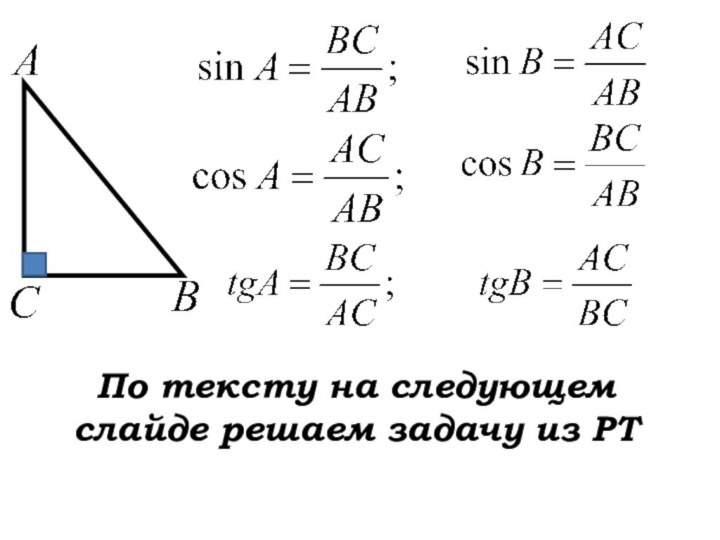
- 29. По тексту на следующем слайде решаем задачу из РТ
- 30. Задания из РТУстная проверка
- 31. По чертежам на карточке записатьсинусы, косинусы
- 32. Работа в парахНазовите чему равны синусы,
- 33. Можете ли вы назвать чему равны синусы, косинусы и тангенса острых углов треугольника ABC?Почему?
- 34. Стр.159, №591(а,в)Прочитайте задание.Как предлагаете его выполнять?Все ли известно?Как найти неизвестные элементы?
- 35. Стр.159, №591(а,в)Решение:а)
- 36. Стр.159, №591(а,в)Решение:а)Найдите самостоятельно в парах синус, косинус и тангенсугла А Проверка
- 37. Стр.159, №591(а,в)Решение:а)Найдите самостоятельно в парах синус, косинус и тангенс угла В Проверка
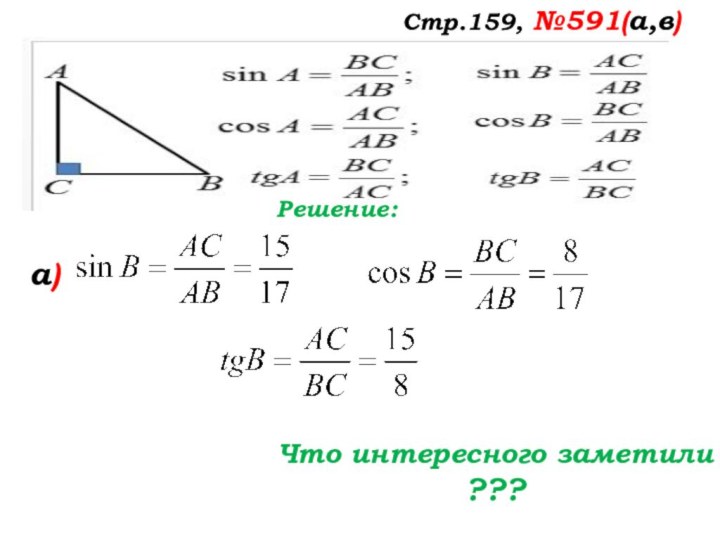
- 38. Стр.159, №591(а,в)Решение:а)Что интересного заметили ???
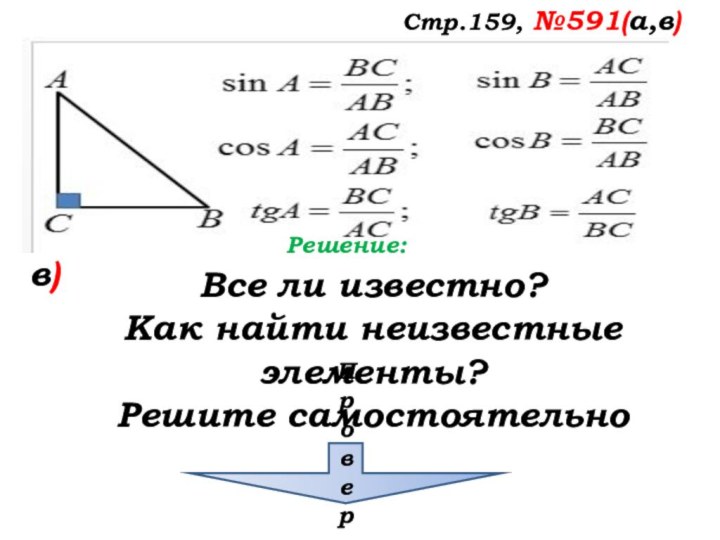
- 39. Стр.159, №591(а,в)Решение:в)Все ли известно?Как найти неизвестные элементы?Решите самостоятельноПроверка
- 40. Стр.159, №591(а,в)Решение:в)Подтвердились ли выводы по заданию а) ?
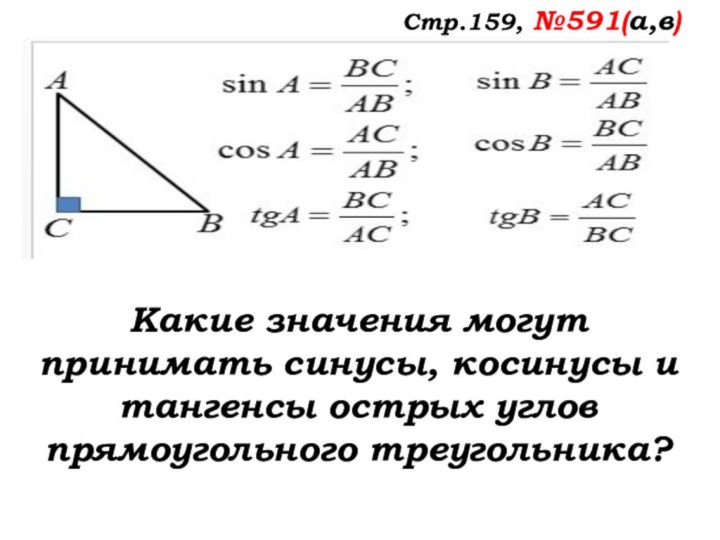
- 41. Стр.159, №591(а,в)Какие значения могут принимать синусы, косинусы и тангенсы острых углов прямоугольного треугольника?
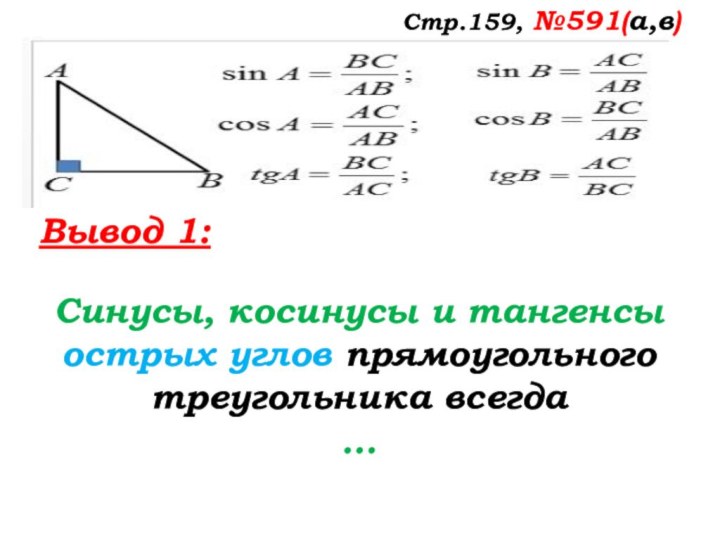
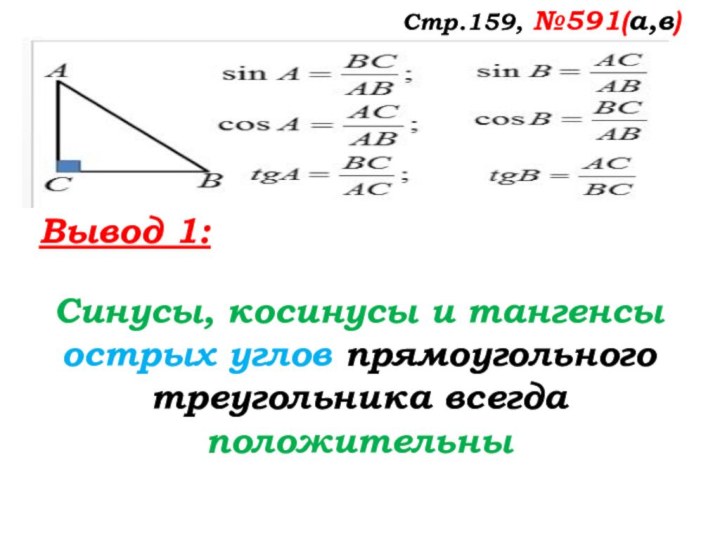
- 42. Стр.159, №591(а,в)Вывод 1:Синусы, косинусы и тангенсы острых углов прямоугольного треугольника всегда …
- 43. Стр.159, №591(а,в)Вывод 1:Синусы, косинусы и тангенсы острых углов прямоугольного треугольника всегда положительны
- 44. Используя формулы,а) найдите самостоятельно и
- 45. Используя формулы,а)иЧто такое для угла А
- 46. Используя формулы,а) иили Прочитайте полученное равенство.Чему равен тангенс угла В?
- 47. Вывод 1:Синусы, косинусы и тангенсы острых углов прямоугольного треугольника всегда положительныВывод 2:
- 48. Используя формулы,б) найдите, комментируя и
- 49. Используя формулы,б)и
- 50. Используя формулы,б)и
- 51. Используя формулы,б)и
- 52. Используя формулы,б)иимеем:
- 53. Используя формулы,б)иимеем:
- 54. б)Основное тригонометрическое тождество. Как записать его для угла В?
- 55. Вывод 1:Синусы, косинусы и тангенсы острых углов прямоугольного треугольника всегда положительныВывод 2:Вывод 3:
- 56. Устно1.Найдите:а)б)в)
- 57. Используя формулы,2.Найдите:а) если
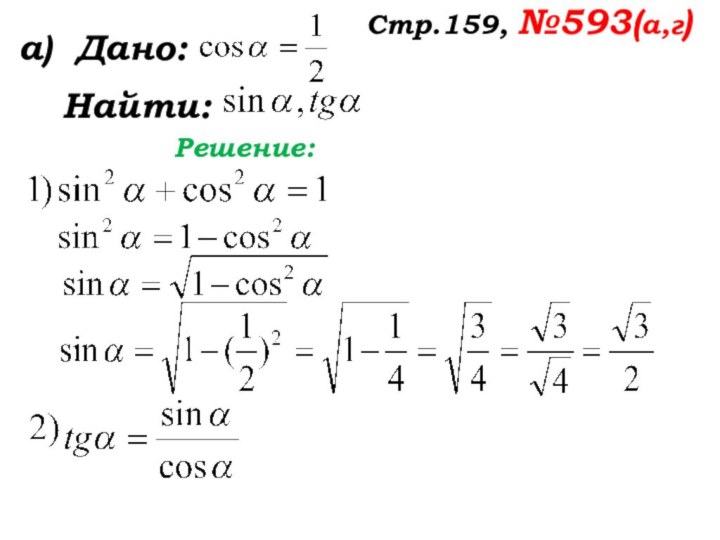
- 58. Стр.159, №593(а,г)а) Дано: Найти: Решение: Какие формулы надо использовать, чтобы найти требуемое?
- 59. Стр.159, №593(а,г)а) Дано: Найти: Решение: Что нужно выразить?
- 60. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 61. Стр.159, №593(а,г)а) Дано: Найти: Решение: !!!
- 62. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 63. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 64. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 65. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 66. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 67. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 68. Стр.159, №593(а,г)а) Дано: Найти: Решение:
- 69. Стр.159, №593(а,г)а) Дано: Найти: Решение: Ответ:
- 70. Стр.159, №593(г)г) Дано: Найти: Решение: Решите самостоятельно, обсудив ход решения
- 71. Стр.159, №593(г)г) Дано: Найти: Решение:
- 72. Стр.159, №593(г)г) Дано: Найти: Решение: Ответ:
- 73. Задача из заданий из МФТИВ окружности
- 74. Задача из заданий из МФТИВ окружности
- 75. Задача из заданий из МФТИВ окружности
- 76. Задача из заданий из МФТИВ окружности
- 77. Критерии
- 78. Назовите
- 79. Скачать презентацию
- 80. Похожие презентации
Приветствую вас на уроке геометрии в 8 классе Уроки №59-6006.02.2017 г.
















































Слайд 3
Успешного усвоения материала
Интересные мысли
и высказывания
Геометрия
приближает разум к истине
Платон
Слайд 5 КР№4 – 16 февраля.
ДР №38 на 06.02.17
Теория:
Cтр.160-161, вопросы 1-14Разобрать задачу № 584.
Решить №585
Слайд 17 Ввести понятие синуса, косинуса и тангенса острого угла
прямоугольного треугольника.
Познакомиться с основным тригонометрическим тождеством и показать его
применение при решении задач.Формировать навыки парной и групповой работы на уроке в процессе решения задач.
Цели урока:
Слайд 19
Стр.156, п.66
Прочитайте определение синуса острого угла
прямоугольного треугольника.
Что нужно знать, чтобы указать чему будет равен
синус острого угла прямоугольного треугольника?синус угла
Слайд 23
Стр.156, п.66
Прочитайте определение косинуса острого угла
прямоугольного треугольника.
Что нужно знать, чтобы указать чему будет равен
косинус острого угла прямоугольного треугольника?косинус угла
Слайд 26
Стр.156, п.66
Прочитайте определение тангенса острого угла
прямоугольного треугольника.
Что нужно знать, чтобы указать чему будет равен
тангенс острого угла прямоугольного треугольника?тангенс угла
Слайд 31
По чертежам на карточке записать
синусы, косинусы и
тангенсы острых углов прямоугольных треугольников
Работа в парах
Устная проверка
Слайд 32
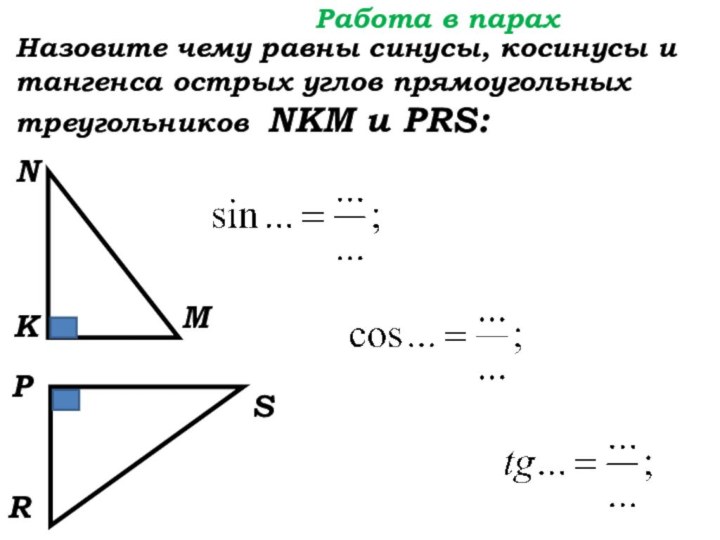
Работа в парах
Назовите чему равны синусы, косинусы
и тангенса острых углов прямоугольных треугольников NKM и PRS:
N
К
М
Р
R
S
Слайд 33
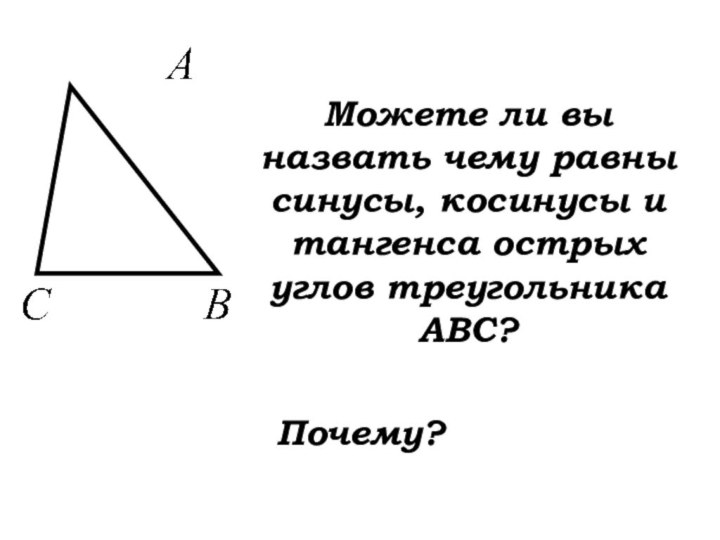
Можете ли вы назвать чему равны синусы,
косинусы и тангенса острых углов треугольника ABC?
Почему?
Слайд 34
Стр.159, №591(а,в)
Прочитайте задание.
Как предлагаете его выполнять?
Все ли
известно?
Как найти неизвестные элементы?
Слайд 36
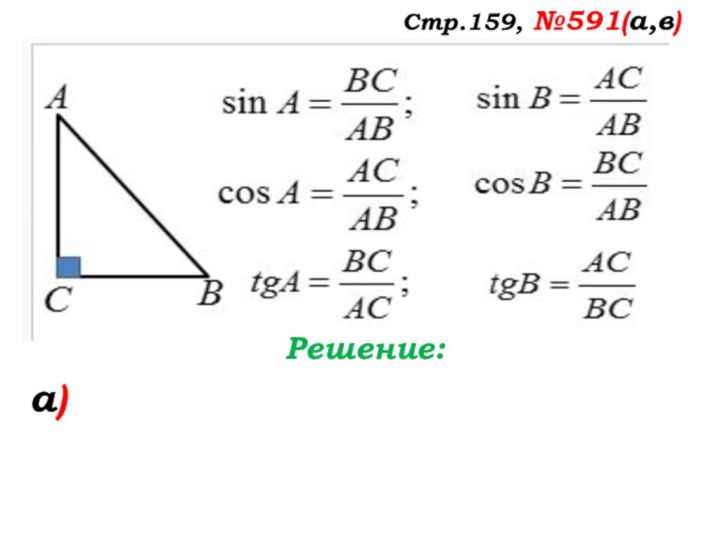
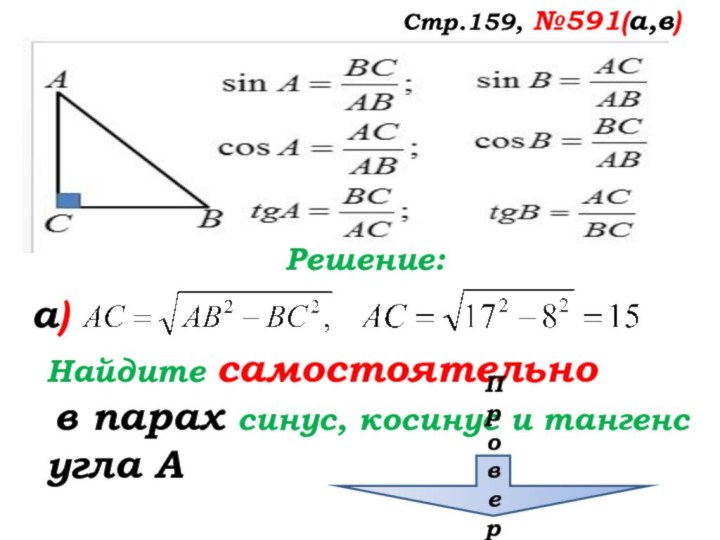
Стр.159, №591(а,в)
Решение:
а)
Найдите самостоятельно
в парах синус, косинус
и тангенс
угла А
Проверка
Слайд 37
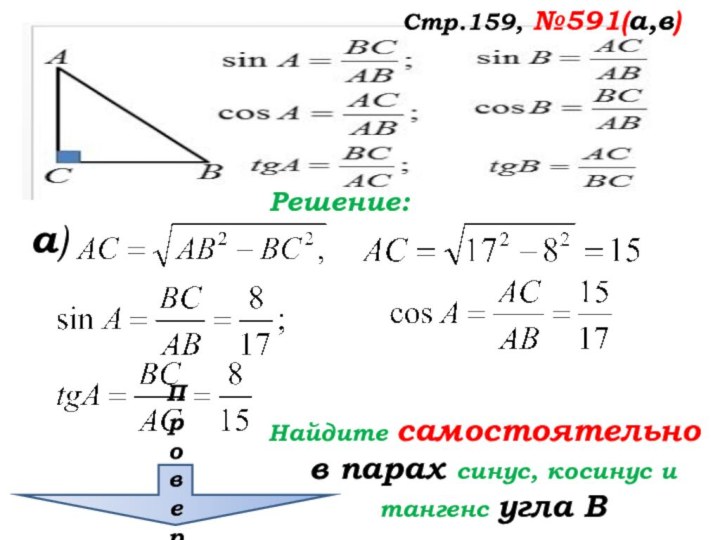
Стр.159, №591(а,в)
Решение:
а)
Найдите самостоятельно
в парах синус, косинус
и тангенс угла В
Проверка
Слайд 39
Стр.159, №591(а,в)
Решение:
в)
Все ли известно?
Как найти неизвестные элементы?
Решите
самостоятельно
Проверка
Слайд 41
Стр.159, №591(а,в)
Какие значения могут принимать синусы, косинусы
и тангенсы острых углов прямоугольного треугольника?
Слайд 42
Стр.159, №591(а,в)
Вывод 1:
Синусы, косинусы и тангенсы острых
углов прямоугольного треугольника всегда
…
Слайд 43
Стр.159, №591(а,в)
Вывод 1:
Синусы, косинусы и тангенсы острых
углов прямоугольного треугольника всегда положительны
Слайд 47
Вывод 1:
Синусы, косинусы и тангенсы острых углов
прямоугольного треугольника всегда положительны
Вывод 2:
Слайд 55
Вывод 1:
Синусы, косинусы и тангенсы острых углов
прямоугольного треугольника всегда положительны
Вывод 2:
Вывод 3:
Слайд 58
Стр.159, №593(а,г)
а) Дано:
Найти:
Решение:
Какие формулы
надо использовать, чтобы найти требуемое?
Слайд 73
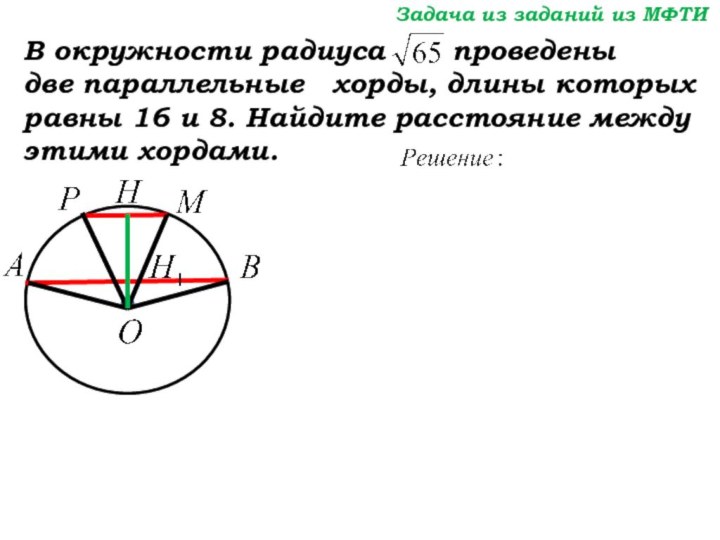
Задача из заданий из МФТИ
В окружности радиуса
проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между этими хордами.
Слайд 74
Задача из заданий из МФТИ
В окружности радиуса
проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между этими хордами.
Слайд 75
Задача из заданий из МФТИ
В окружности радиуса
проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между этими хордами.
Слайд 76
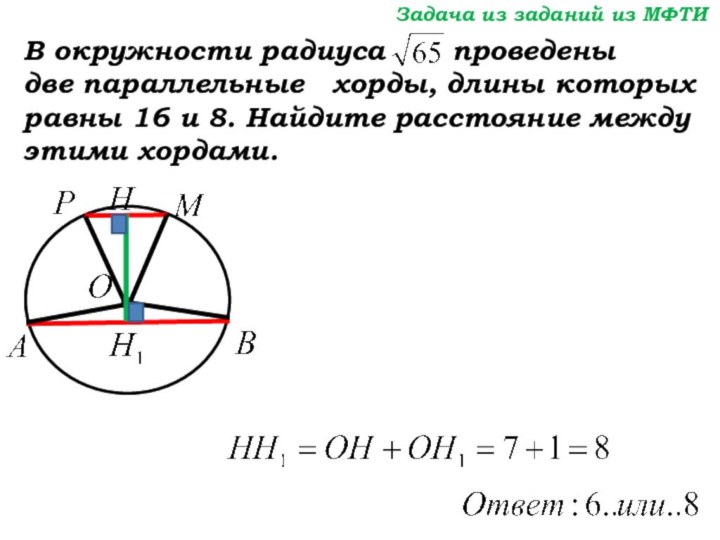
Задача из заданий из МФТИ
В окружности радиуса
проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между этими хордами.
Слайд 77
Критерии
оценки за урок:
1. Комментировали ДЗ
2. Активно участвовали в решении
устных задач.3. Привели решение задач, решаемых письменно
Поставьте себе оценку за урок