- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Скалярное произведение векторов
Содержание
- 2. αОУгол между векторами
- 3. 300 3001200 900 1800 00 Найдите угол между векторами
- 4. Скалярное произведение векторов – число (скаляр).Скалярным произведением
- 5. = 0 Скалярное произведение ненулевых векторов равно
- 6. Скалярное произведение ненулевых векторов положительно тогда и
- 7. Скалярное произведение ненулевых векторов отрицательно тогда и
- 8. cos 001cos1800-1Частный случай №4
- 9. cos00 1Таким образом, скалярный квадрат вектора равен
- 10. Все ребра тетраэдра АВСD равны друг
- 11. Формула для нахождения скалярного произведениячерез координаты векторов= x1x2 + y1y2 + z1z2
- 12. Пример №1Найти скалярное произведение векторов:a {-6; 9; 5}b {-1; 0; 7}
- 13. Пример №2Найти скалярное произведение векторов:a {0; 0; 4}b {22; 1; 8}
- 14. Пример №3Найти скалярное произведение векторов:a {1; 7; 9}b {-2; 4; 0}
- 15. Проверочная работа1. Найти скалярное произведение векторов:a {1; 10; 7}b {0; 7; 0}
- 16. Проверочная работа2. Найти скалярное произведение векторов:a {7; 25; 0}b {11; 0; 54}
- 17. Проверочная работа3. Найти скалярное произведение векторов:a {|-2|; 0; |3|}b {1; |-11|; 1}
- 18. Проверочная работа4. Найти скалярное произведение векторов:a {sin(900); 2; 3}b {3; 2; 1}
- 19. Проверочная работа5. Найти скалярное произведение векторов:a {-1; 2; 8}b {5; 5; 0}
- 20. Проверочная работаРабота закончена.Перейдём к проверке.
- 21. Проверочная работа1. Найти скалярное произведение векторов:a {1; 10; 7}b {0; 7; 0}
- 22. Проверочная работа2. Найти скалярное произведение векторов:a {7; 25; 0}b {11; 0; 54}
- 23. Проверочная работа3. Найти скалярное произведение векторов:a {|-2|; 0; |3|}b {1; |-11|; 1}
- 24. Проверочная работа4. Найти скалярное произведение векторов:a {sin(900); 2; 3}b {3; 2; 1}
- 25. Проверочная работа5. Найти скалярное произведение векторов:a {-1; 2; 8}b {5; 5; 0}
- 26. Скачать презентацию
- 27. Похожие презентации
αОУгол между векторами
























Слайд 4
Скалярное произведение векторов – число (скаляр).
Скалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
Определение
Слайд 5
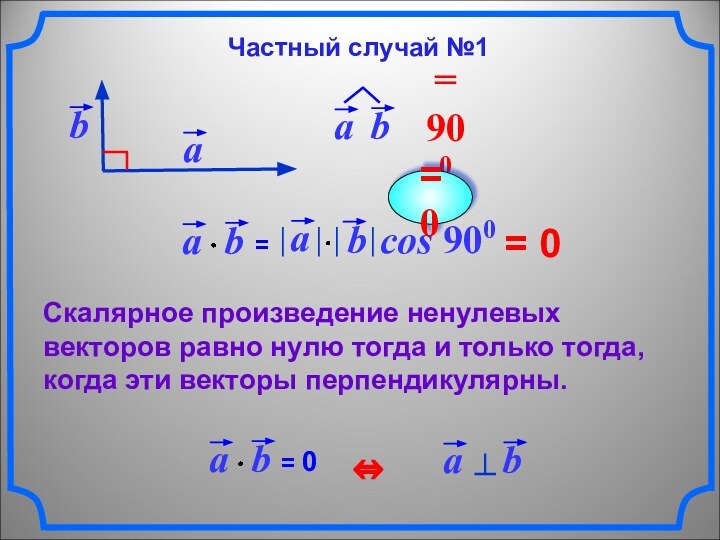
= 0
Скалярное произведение ненулевых векторов равно нулю
тогда и только тогда, когда эти векторы перпендикулярны.
Частный случай
№1= 0
Слайд 6
Скалярное произведение ненулевых векторов положительно тогда и только
тогда, когда угол между векторами острый.
cos
α
> 0
> 0
Частный случай №2
Слайд 7
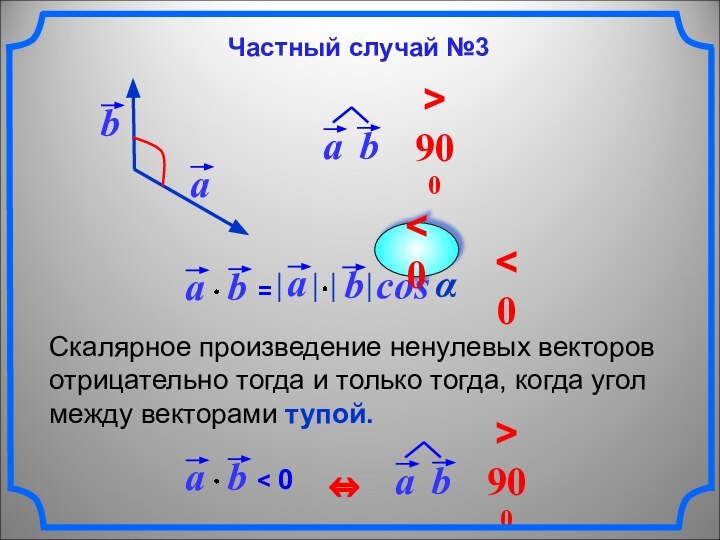
Скалярное произведение ненулевых векторов отрицательно тогда и только
тогда, когда угол между векторами тупой.
cos
α
< 0
< 0
Частный случай №3
Слайд 9
cos
00
1
Таким образом,
скалярный квадрат вектора равен квадрату
его длины.
Частный случай
№52
2
2
2
Слайд 10 Все ребра тетраэдра АВСD равны друг другу.
Точки М и
N – середины ребер АD и
ВС. Докажите, что B
C
N
A
D
M
Задача