Презентация на тему Признак параллельности прямой и плоскости

не пересекаются.
Теорема 1.1
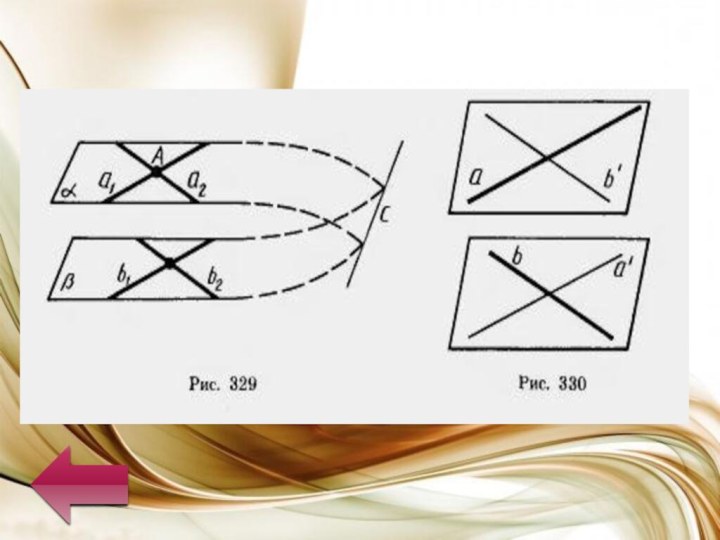
Если две пересекающиеся прямые одной плоскости соответственно

параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство. Пусть α и β— данные плоскости, а1 и a2 — прямые в плоскости α , пересекающиеся в точке А, b1, и b2 — соответственно параллельные им прямые в плоскости β. Допустим, что плоскости α и β не параллельны, т. е. пересекаются по некоторой прямой с. По теореме 1.1 прямые а1 и a2, как параллельные прямым b1и b2, параллельны плоскости β и поэтому они не пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости α через точку А проходят две прямые (а1 и a2), параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию. Теорема доказана.

основе теоремы, согласно которой, два проведенных перпендикуляра по отношению

к одной прямой, будут параллельны. Существуют определенные признаки параллельности прямых – всего их три, и все их мы рассмотрим более конкретно.

третьей прямой, образуемые внутренние углы, лежащие накрест, будут равны.
Допустим,

при пересечении прямых АВ и СD прямой линией ЕF, были образованы ∠1 и ∠2. Они равны, так как прямая линия ЕF проходит под одним уклоном по отношению к двум остальным прямым. В местах пересечения линий, ставим точки К и L – у нас получился отрезок секущей ЕF. Находим его середину и ставим точку О

На прямую АВ опускаем перпендикуляр из точки О. Назовем его ОМ. Продолжаем перпендикуляр до тех пор, пока он не пересечется с прямой СD. В результате, первоначальная прямая АВ строго ⊥ МN, а это значит, что и СD ⊥ МN, но это утверждение требует доказательства. В результате проведения перпендикуляра и линии пересечения, у нас образовалось два треугольника. Один из них – МОЕ, второй – NОК.

теоремы, ∠1 =∠2, а в соответствии с построением треугольников,

сторона ОK = стороне ОL. ∠ МОL = ∠NОК, поскольку это вертикальные углы. Из этого следует, что сторона и два угла, прилежащие к ней одного из треугольников соответственно равны стороне и двум углам, прилежащим к ней, другого из треугольников. Таким образом, треугольник МОL = треугольнику NОК, а значит, и ∠LМО = ∠КNО, но нам известно, что LМО прямой, значит, и соответствующий ему, ∠КNО тоже прямой. То есть, нам удалось доказать, что к прямой МN, как прямая АВ, так и прямая СD перпендикулярны. То есть, АВ и СD по отношению друг к другу являются параллельными. Это нам и требовалось доказать.

необходимо доказать, что углы, полученные в процессе пересечения параллельных

прямых АВ и СD прямой ЕF, будут равны. Таким образом, признаки параллельности двух прямых, как первый, так и второй, основывается на равности углов, получаемых при пересечении их третьей линией. Допускаем, что ∠3 =∠ 2, а ∠1 = ∠3, поскольку он вертикален ему. Таким образом, и ∠2 будет равен ∠1, однако следует учитывать, что как ∠1, так и угол 2 являются внутренними, накрест лежащими углами. Следовательно, нам остается применить свои знания, а именно то, что два отрезка будут параллельными, если при их пересечении третьей прямой образованные, накрест лежащие углы будут равными. Таким образом, мы выяснили, что АВ || СD.

Нам удалось доказать, что при условии параллельности двух перпендикуляров к одной прямой, согласно соответствующей теореме, признак параллельности прямых очевиден.