Презентация на тему по геометрии на тему Свойство биссектрисы равнобедренного треугольника (7 класс)

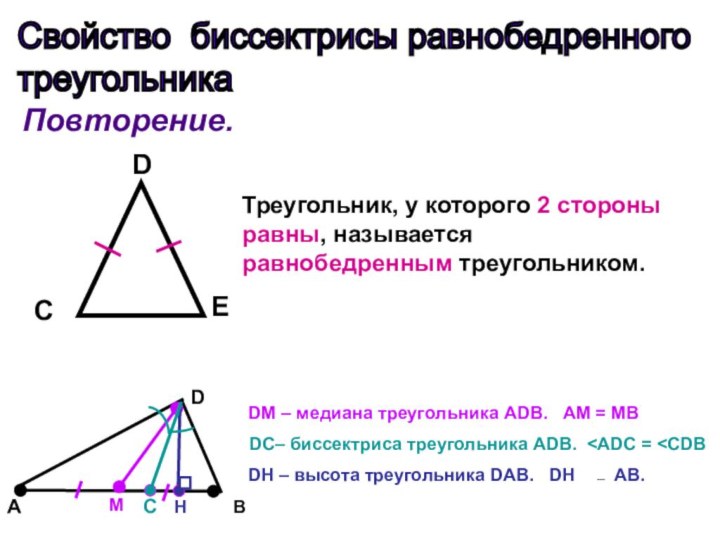
равны, называется равнобедренным треугольником.
D

С
E

B
D
A
C


H
M
DM – медиана треугольника АDВ.

DC– биссектриса треугольника АDВ.

DH – высота треугольника DAB. DH AB.

является медианой и высотой.

A
С
B
Дано: ABC –

Доказательство.

1

2

1) В ABD и DBC известно:
AB = BC (по условию)
BD = BD (общая)
< 1 = < 2 (BD – биссектриса)
ABD = ВDС ( СУС)

2) В равных треугольниках против равных углов лежат равные стороны. Значит, АD = DС. Следовательно, BD- медиана ABC.

D

Свойство биссектрисы равнобедренного треугольника

3) ABD = ВDС. Отсюда < 3 = < 4

4

3

< 3 и < 4 - смежные

< 3 = 90о; < 4 = 90о.

Значит, BD AC.

Следовательно, BD - высота ABC

стороны ВС и АВ равны, BD – медиана,

A

С

B

D

Дано: ABC; AB = BC; BD – медиана, < АВС = 40 о
Найти : < DBC и < BDC.

Решение.

1) В АВС известно, что АВ = ВС, значит, АВС - равнобедренный.

2) BD – медиана в равнобедренном АВС, проведенная к основанию,
значит, ВD - биссектриса. Следовательно, < DBC = ½ * < ABC = ½*40o = 20o

3) BD – медиана в равнобедренном АВС, проведенная к основанию,
значит, ВD - высота. Следовательно, BD AC. Отсюда < BDC = 90o

40о