Презентация на тему Об углах между скрещивающимися прямыми

одна из которых проходит по эстакаде, а другая под

эстакадой.

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

методов в практике.

Рассмотрение различных способов определения угла между скрещивающимися

прямыми

Цель и задачи работы

лучами (сторонами угла), выходящими из одной точки (которая называется

вершиной угла).

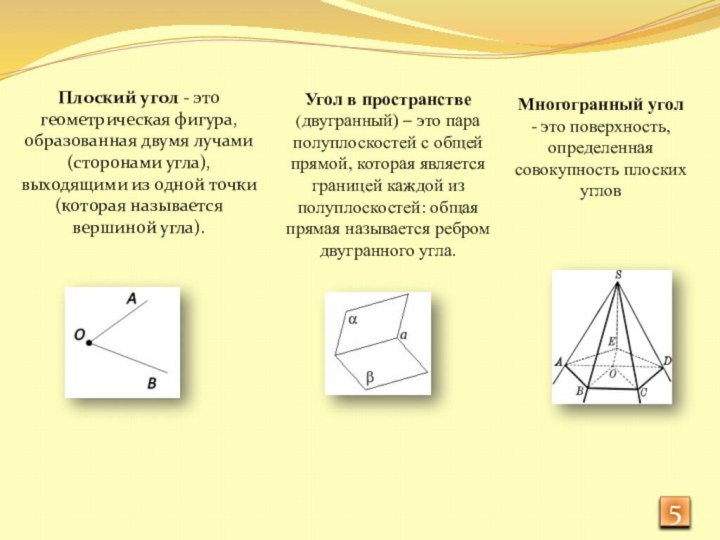
Угол в пространстве (двугранный) – это пара полуплоскостей с общей прямой, которая является границей каждой из полуплоскостей: общая прямая называется ребром двугранного угла.

Многогранный угол - это поверхность, определенная совокупность плоских углов

точки, мера всевозможных направлений.

соответственно, по-разному фиксируются его границы
Угол между двумя лучами с

общим началом лежит в границах от 0 до .
Угол между двумя прямыми лежит в границах от 0 до /2 .
Угол между двумя отрезками (например, диагонали четырехугольника), лежит в границах от 0 до /2.
Угол между двумя нулевыми векторами лежит в границах от 0 до .
Угол между двумя осями лежит в границах от 0 до .
Угол между прямой и осью лежит в границах от 0 до .
Угол между нулевым вектором и осью лежит в границах от 0 до .
Двугранных угол лежит в границах от 0 до .

от 0 до /2
Угол между двумя плоскостями лежит

в границах от 0 до /2.
Угол между пересекающимися прямой и кривой, расположенными в одной плоскости, лежит в границах от 0 до /2.
Угол между двумя пересекающимися кривыми лежит в границах от 0 до /2.
Угол между двумя лучами, не имеющими общего начала , лежит в границах от 0 до .
Угол между двумя скрещивающимися прямыми лежит в границах от 0 до /2.
Угол между двумя отрезками, лежащими на скрещивающихся прямых , лежит в границах от 0 до /2 .
Угол поворота лежит в границах от 0 до .

Теорема о вертикальных углах .
3. Теорема о сумме

углов треугольника.
4. Теорема о сумме углов многоугольника.
5.Теорема об углах с соответственно параллельными (перпендикулярными) сторонами.
6. Теоремы об углах, полученных при пересечении параллельных прямых секущей.
7. Признаки равенства треугольников.
8. Признаки подобия треугольников.
9.Теорема косинуса.
10. Теорема синусов.
11. Теоремы об углах, связанных с окружностью.
12. Теорема косинусов для трехгранного угла.
13.Теорема синусов для треxгранноrо угла.

скрещивающихся прямых.






Задачи на вычисление угла между скрещивающимися

прямыми.

скрещивающимися прямыми
Способ опирающийся на перпендикулярность двух плоскостей
Способ опирающийся на

параллельность прямой и плоскости
Способ – использование теоремы о трех перпендикулярах
Способ – проектирование двух точек одной прямой на другую прямую
Способ – векторный

Задачи на установление перпендикулярности скрещивающихся прямых

ли прямые KB1 и RH1?
Решение. Построим плоскость KB1M ,

где точка M середина СС1 . Сечение KB1MD – является ромбом. RH параллельна прямой A1C1 , а A1C1 параллельна прямой KM, следовательно прямые RH и KM параллельны. Значит, KM – параллельная проекция RH на плоскость KB1M. А так как прямые KM и KB1 не перпендикулярны, то не будут перпендикулярны и прямые RH и KB1.

другую прямую
Задача. Перпендикулярны ли прямые B1D и A1O?

Решение. Спроектируем

две точки прямой B1D на прямую A1O. Для простоты возьмем точки B1 и D. Проекцией D будет точка O . Проекцию точки В1 найдем в два приема. Сначала спроектируем точку B1 на плоскость AA1С1 (в ней лежит прямая A1O); проекцией будет точка O1. Затем O1, спроектируем в плоскости AA1С1 на прямую A1O. Проекцией будет какая-то точка X, лежавшая внутри отрезка A1O. Согласно теореме о трех перпендикулярах ( в слегка измененной формулировке) точка X и будет проекцией точки B1 на прямую A1O. Мы видим, что проекции точек B1 и D на прямую A1O не совпадают, следовательно, прямые B1D и A1O не перпендикулярны.

с помощью параллельного переноса
Способ – «в три косинуса»
Способ –

проектирование обеих скрещивающихся прямых на плоскость
Способ – проектирование отрезка одной из скрещивающихся прямых на другую
Способ– векторный
Способ– « с помощью замкнутой ломаной»
Способ – «с помощью тетраэдра»
Способ– координатный

cosp1q
Задача. Перпендикулярны ли прямые CD1 и BC1 ?

Решение. Чтобы

найти угол между прямыми CD1 и BC1, спроектируем CD1 на плоскость грани BCC1B1. Проекцией будет прямая CC1. Дальше только вычисления по формуле:
cos(CD1, BC1) = cos(CD1, CC1)  cos(CC1, BC1 ).
cos(CD1, BC1) = * = Искомый угол равен 60, прямые CD1 и BC1 не перпендикулярны.

CD1?
Бескоординатный вариант
Представим вектор как сумму

векторов и а вектор как сумму векторов и Затем, считая куб единичным, найдем скалярное произведение векторов А1D и D1C
,


И наконец, разделим полученный результат на произведение длин этих векторов (а длина каждого равна ). В итоге получим косинус угла между векторами А1D и D1C , равный , и сам угол — 60.