Презентация на тему Проекции прямой

точки А и В, лежащие на этой прямой. Это

Пространственная картина

Проекции прямой

точек: горизонтальная проекция прямой m1 – через А1 и

x

Пространственная картина

Комплексный чертеж

Проекции прямой

проводят постоянную чертежа k под углом 45. С ее

k

45

Безосным называется чертеж, на котором
отсутствуют оси проекций

Безосный чертеж

45

– угол наклона отрезка к плоcкости П1 ;


B

A

Положение прямой относительно плоскостей проекций

Н.в.

искаженные метрические характеристики, ни одна из ее проекций не

Прямая общего положения наклонена ко всем плоскостям проекций

Прямая общего положения

натуральные величины каких-либо ее характеристик. Прямая уровня про-ецируется без

Прямая частного положения параллельна или перпендикулярна одной из плоскостей проекций

Прямая, параллельная одной из плоскостей проекций, называется прямой уровня:
Горизонтальная прямая уровня (горизонталь) h  П1
Фронтальная прямая уровня (фронталь) f  П2
Профильная прямая p П3

Прямая, перпендикулярная одной из плоскостей проекций, называется проецирующей прямой:
Горизонтально проецирующая прямая  П1
Фронтально проецирующая прямая  П2
Профильно проецирующая прямая  П3

Прямые частного положения

про-екций П1 и имеют одинаковую аппликату z= const. Фронтальная

Пространственная картина

Комплексный чертеж

x

h

B

A

Прямые уровня: горизонталь (h П1)

точки прямой АВ равноудалены от фронтальной плоскости проекций П2

проекций П3 и имеют одинаковую координату х (х= const).

Пространственная картина

Комплексный чертеж

z

O

x

y1

y3

B

A

р

Прямые уровня: профильная прямая (р П3)

П1 , поэтому ее горизонтальная проекция А1 В1

П1 и П3 . Фронтальная проекция А2 В2 вырождается

Пространственная картина

Комплексный чертеж

A

B

x

Фронтально проецирующая прямая (П2)

В3 вырождается в точку. Относительно П1 и П2

Пространственная картина

Комплексный чертеж

B

A

x

z

y1

y3

Профильно проецирующая прямая (П3)

новую плоскость проекций П4 , которой прямая АВ будет

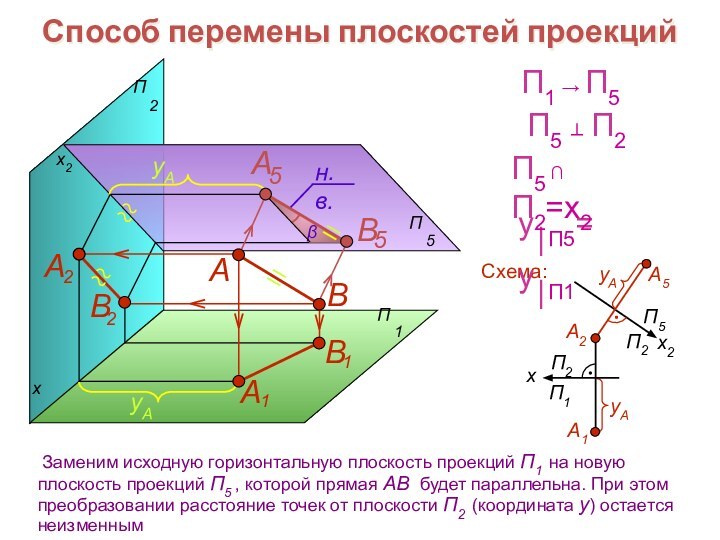
Способ перемены плоскостей проекций

Схема:

 П2
П5  П2=x2
Заменим исходную горизонтальную плоскость

к плоскостям проекций (способ замены плоскостей проекций)
Ось х1

наклона к плоскостям проекций
x
А1
B1
А2
B2
П2
П1
x1
П4
П1
А4
В4

Ось х2 новой плоскости проекций

наклона к плоскостям проекций

наклона к плоскостям проекций

наклона к плоскостям проекций
Данный отрезок АВ занимает общее положение,

наклона к плоскостям проекций

наклона к плоскостям проекций
Схема:

точку
B
A
D
C
K
x
C
2
АВ  СD = K(К1 , К2)
А1 В1 

А2 В2  С2 D2 = K2

Точка пересечения К прямых АВ и СD проецируется в точки пересече-ния соответствующих проекций прямых: на П1 - это точка К1 ; на П2 - точка К2 . Точки пересечения К1 и К2 одноименных проекций прямых лежат на одной линии связи

точек
Проекции параллельных прямых не пересекаются. Одноименные проекции прямых параллельны

n

m

x

n

1

m  n

m1  n1

m2  n2

и
не параллельны между собой
Проекции скрещивающихся прямых могут быть

m

n

m1  n1

m2  n2

прямого угла параллельна плоскости проекций, а другая ей не

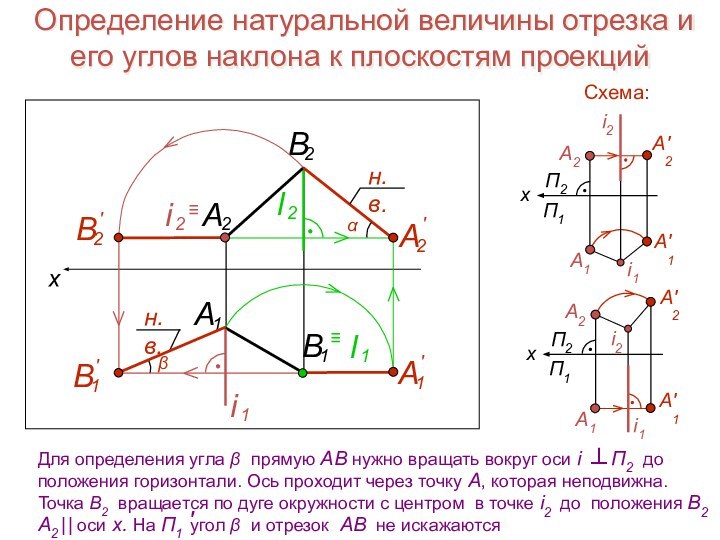
Для доказательства продолжим сторону угла АВ до пересечения с ее проекцией А1 В1 в точке М1 . Через точку М1 проведем прямую М1 N1  В1 C1 .
Т. к. BC П1 , то BC В1 С1 . Значит, М1 N1 ВС и BM1 N1 =90 . По теореме о 3-х перпендикулярах B1 M1 N1 =90 , следовательно, и A1 В1 С1 = 1 =90

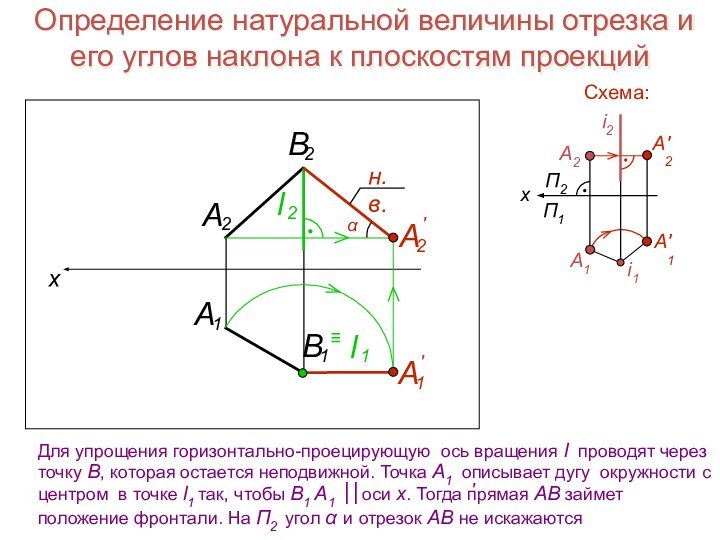
Дано:

Доказать:

изображение прямого угла, то одна из его сторон обязательно

из точки С к прямой f
D2  D1

C2D2  f2

D1  C1

Прямая f является фронталью и проецируется на П2 в натуральную величину. Следовательно, фронтальная проекция перпендикуляра С2 D2 перпендикулярна фронтальной проекции прямой f . Определяем основа-ние перпендикуляра – точку D. Строим горизонтальную проекцию С1 D1

прямой l способом перемены плоскостей проекций
Искомое расстояние есть перпендикуляр.

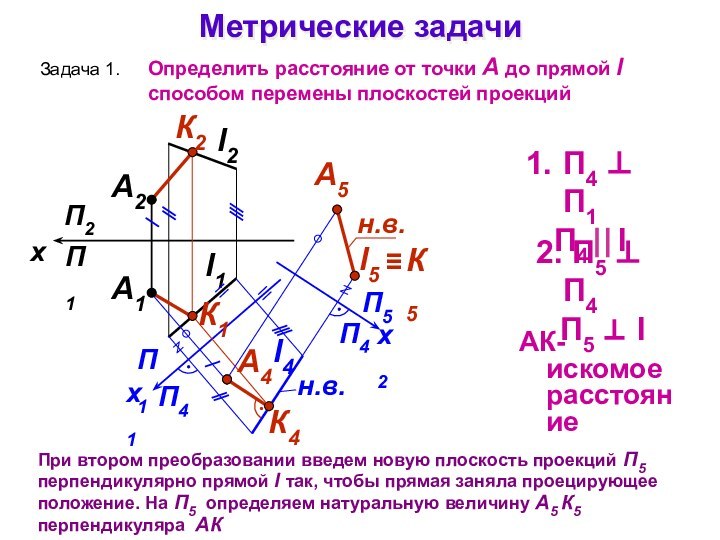
П4  П1
П4 l