его окрестностях геометрическое тело конус и составить задачи для
использования в интерактивных средствах обучения школьников.Задачи:
1. Рассмотрение вариантов применения конуса в отдельных архитектурных объектах нашего города.
2. Составление задач с использованием применяемых типов конусов
3. Решение составленных задач
Объекты исследования: архитектурные здания и строения, выставочные экспонаты г. Севастополя.
Предмет исследования: геометрическая фигура конус
Методы исследования:
1. Наблюдение (рассмотреть многообразие архитектурных сооружений города) .
2. Анализ (проанализировать литературу по исследуемой теме).
3. Сравнительно – описательный (показать в каких объектах встречается конус).
4. Моделирование.
5. Эксперимент.
6. Оформление результатов исследования.




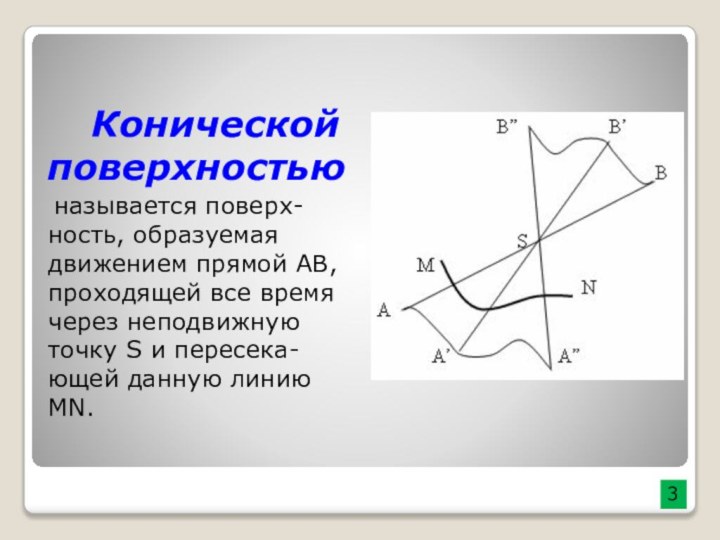
























![Презентация к уроку геометрии 11 класс Конусы вокруг нас Геометрические тела. Конус.- [Электронный ресурс]. - Режим доступа. - www.calc.ru/Geometricheskiye-Tela-Konus.html Конус.-](/img/tmb/7/634215/06631ed638650c7ffc0ae3a1034b6685-720x.jpg)