- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему для интегрированного урока математики и информатики по теме Теорема Пифагора
Содержание
- 2. «Да, путь познания не гладок.Но знаем мы со школьных лет,Загадок больше, чем разгадок,И поискам предела нет!»
- 3. ТЕОРЕМА ПИФАГОРА
- 4. «Геометрия владеет многими сокровищами: одно из них – это теорема Пифагора»
- 5. Цели урока:Образовательные: изучить теорему Пифагора, ее роль
- 6. Теорема Пифагора - одна из важнейших теорем
- 7. СООБЩЕНИЕ О ПИФАГОРЕ
- 8. История теоремы Пифагора В вавилонских текстах она
- 9. История теоремы Пифагора«Пифагоровы штаны во все стороны равны»
- 12. Pons Asinorum - «ослиный мост» elefuga - «бегство убогих»
- 13. «Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик
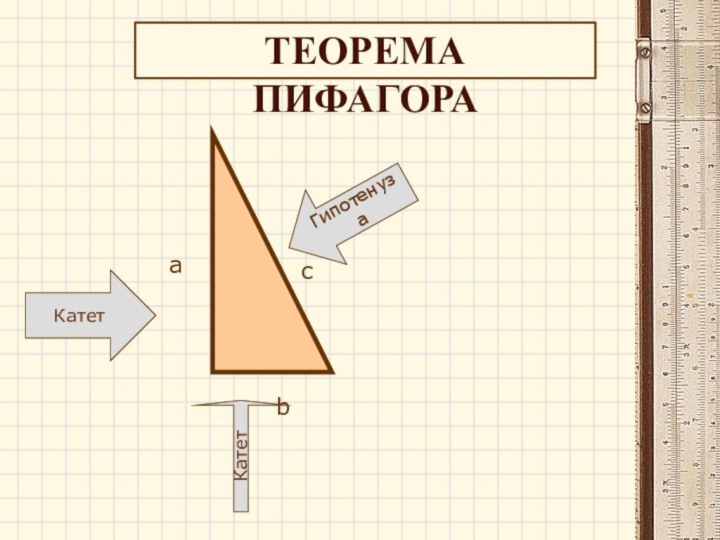
- 14. Это прямоугольный треугольникТЕОРЕМА ПИФАГОРА
- 15. аcbКатетКатетГипотенузаТЕОРЕМА ПИФАГОРА
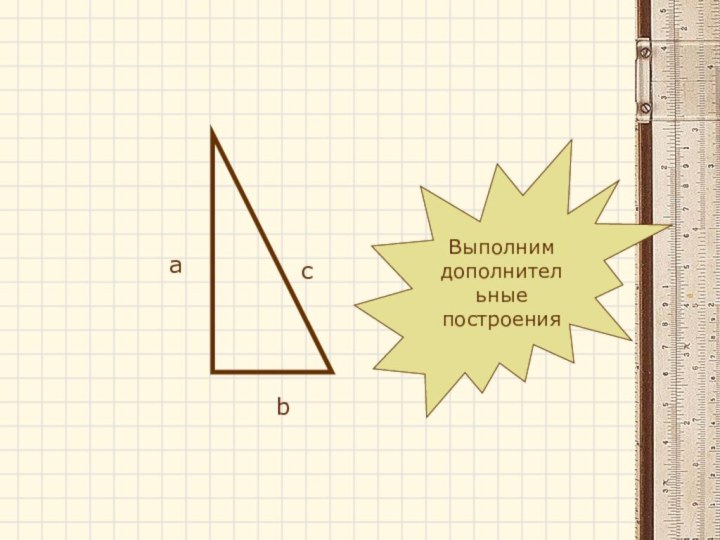
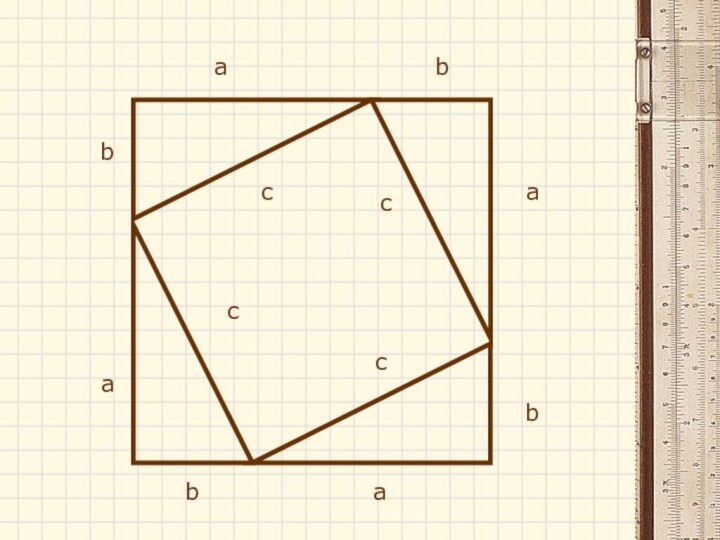
- 16. Выполним дополнительные построенияаcb
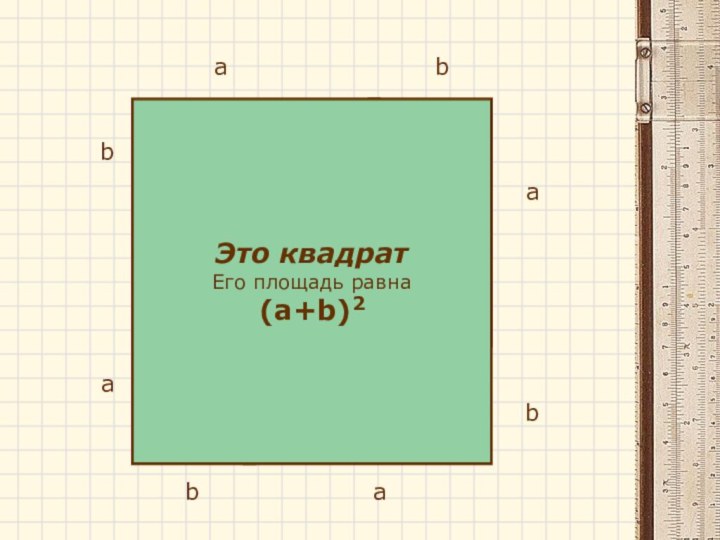
- 18. аcbаааbbbcccЭто квадратЕго площадь равна (а+b)2
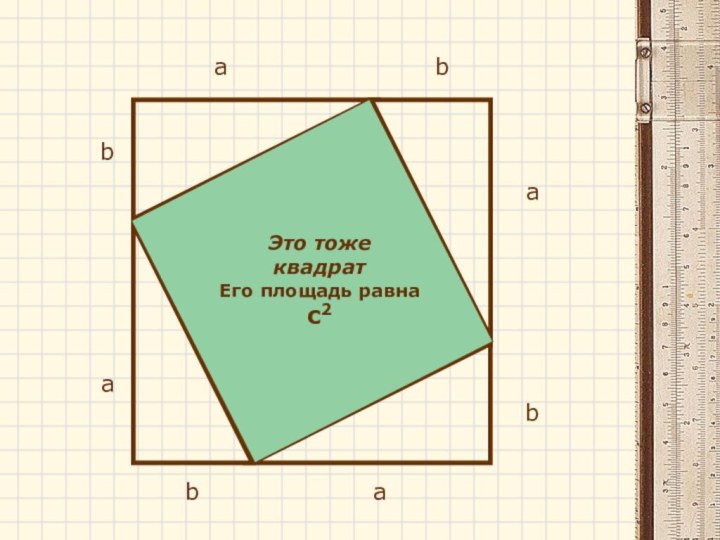
- 19. аcbаааbbbcccЭто тоже квадрат Его площадь равна c2
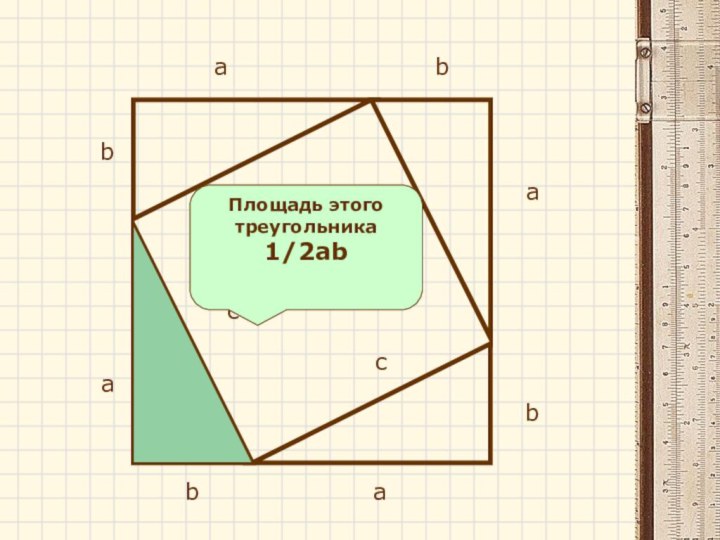
- 20. аcbаааbbbcccПлощадь этого треугольника 1/2аb
- 21. Площадь большого квадрата равна сумме площадей маленького квадрата и площадей 4-х треугольников(a+b)2=c2+4*1/2abОтсюда a2+2ab+b2=c2+2aba2+b2=c2
- 22. Если дан нам треугольникИ притом с прямым
- 23. Сформулируйте теорему ПифагораСформулируйте теорему, обратную теореме ПифагораЕсли
- 24. Дано: ∆АВС, ∆АВС- прямоугольный с
- 25. с² = а2 + b2с=13а=1213² = 122
- 26. Задача «Установи ёлку»86?По теореме Пифагорас² =а² +b²с² = 6² +8²с² = 36 +64с² =100с=10м
- 27. Закрепление изученного материалаРабота с тестом Запись функций и арифметических операций
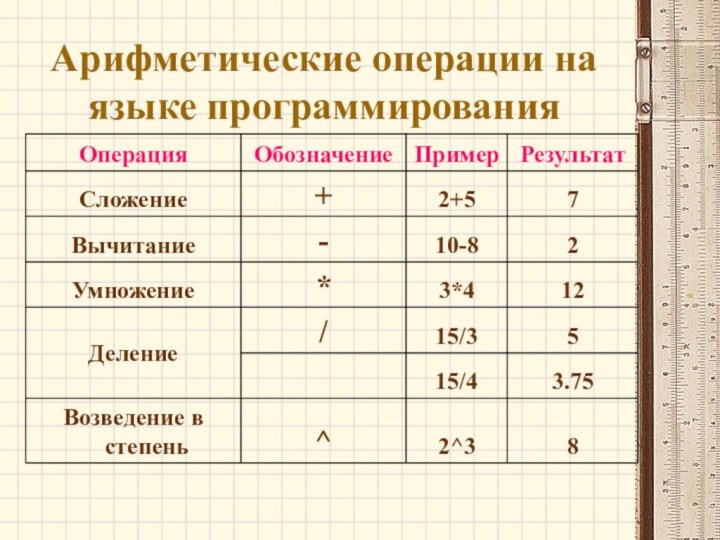
- 28. Арифметические операции на языке программирования
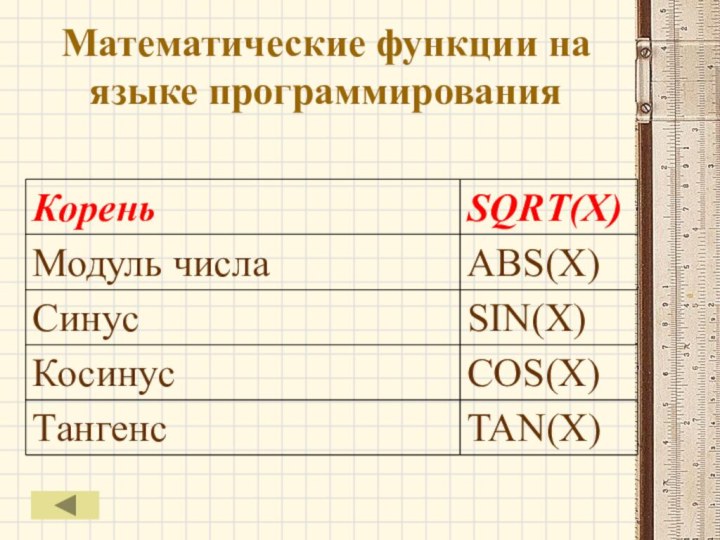
- 29. Математические функции на языке программирования
- 30. Задача индийского математика XII века БхаскарыИСТОРИЧЕСКИЕ ЗАДАЧИ
- 31. Задача из китайской "Математики в девяти
- 32. Задача из учебника "Арифметика" Леонтия Магницкого«Случися
- 33. Причина популярности теоремы Пифагора триедина – это красота, простота и значимость!
- 34. Скачать презентацию
- 35. Похожие презентации




















Слайд 5
Цели урока:
Образовательные:
изучить теорему Пифагора, ее роль в
геометрии, использование теоремы в решении задач;
закрепить умение работать с
операционной системой Windows, прикладными программами этой операционной системы: тестирующей программой My Test, программой создания презентаций, познакомиться с записью арифметических операций и математических функций при вводе формул. Развивающие:
развитие логического мышления, познавательного интереса, творческого поиска, самостоятельности;
формирование умения сравнивать, обобщать изучаемые факты;
развитие у учащихся самостоятельности в мышлении и учебной деятельности;
повысить эмоциональный настрой учащихся путем привлечения наглядности и технических средств обучения (компьютер).
Воспитательные:
воспитание у учащихся ответственного отношения к учению, культуры математической речи;
воспитание коллективизма и ответственности за общую работу;
воспитание взаимопомощи;
воспитание аккуратности
Слайд 6 Теорема Пифагора - одна из важнейших теорем геометрии.
Она является основой
решения множества
геометрических задач
и базой изучения
теоретического
материала в
дальнейшем.
Слайд 8
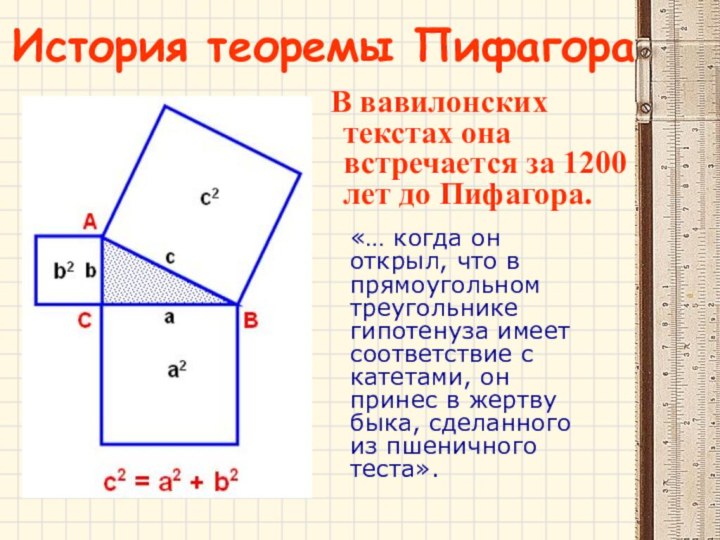
История теоремы Пифагора
В вавилонских текстах она встречается
за 1200 лет до Пифагора.
«… когда он открыл,
что впрямоугольном треугольнике
гипотенуза имеет соответствие с
катетами, он принес в жертву
быка, сделанного из пшеничного
теста».
Слайд 13
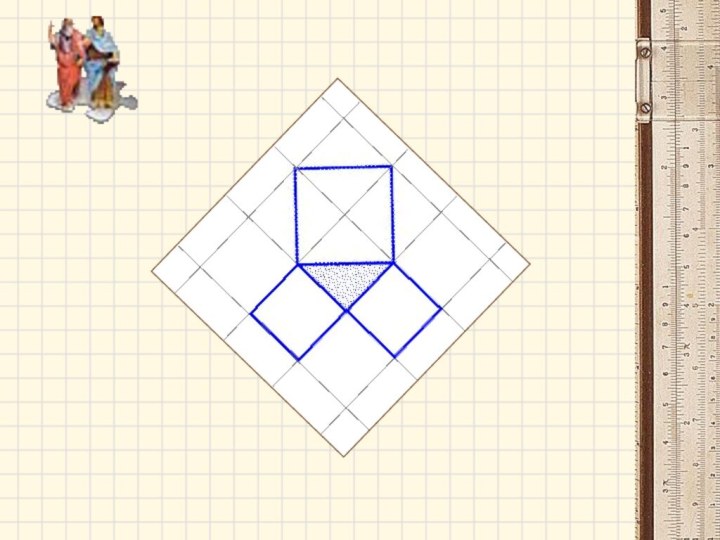
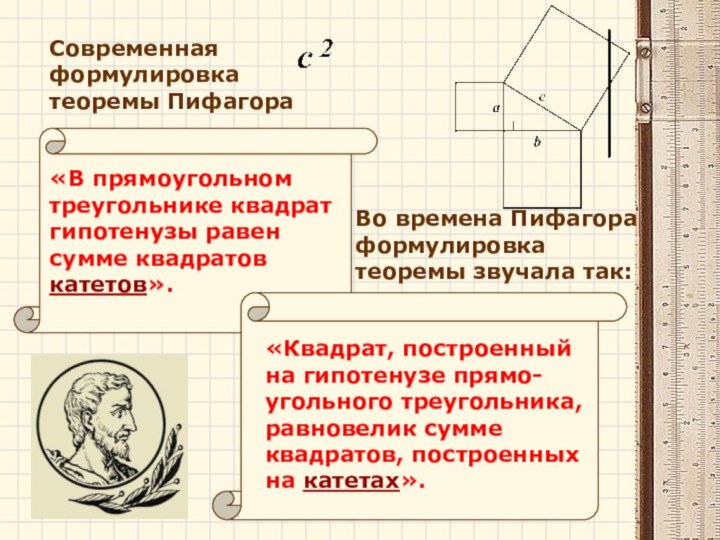
«Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик сумме
квадратов, построенных на катетах».
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме
квадратов катетов».Во времена Пифагора формулировка теоремы звучала так:
Современная формулировка
теоремы Пифагора
Слайд 21
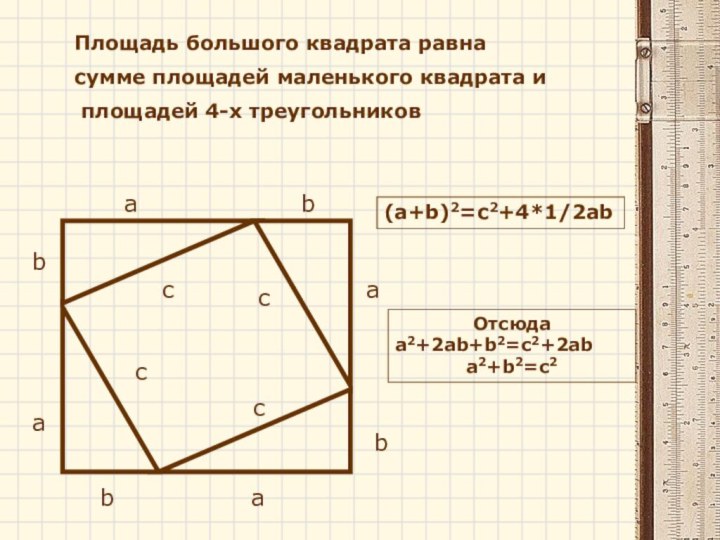
Площадь большого квадрата равна
сумме площадей маленького квадрата
и
площадей 4-х треугольников
(a+b)2=c2+4*1/2ab
Отсюда
a2+2ab+b2=c2+2ab
a2+b2=c2
Слайд 22
Если дан нам треугольник
И притом с прямым углом,
То
квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней
находим —И таким простым путем
К результату мы придем.
И. Дырченко
Слайд 23
Сформулируйте теорему Пифагора
Сформулируйте теорему, обратную теореме Пифагора
Если в
треугольнике квадрат большей стороны равен сумме квадратов двух других
сторон, то этот треугольник будет прямоугольным.
Слайд 24
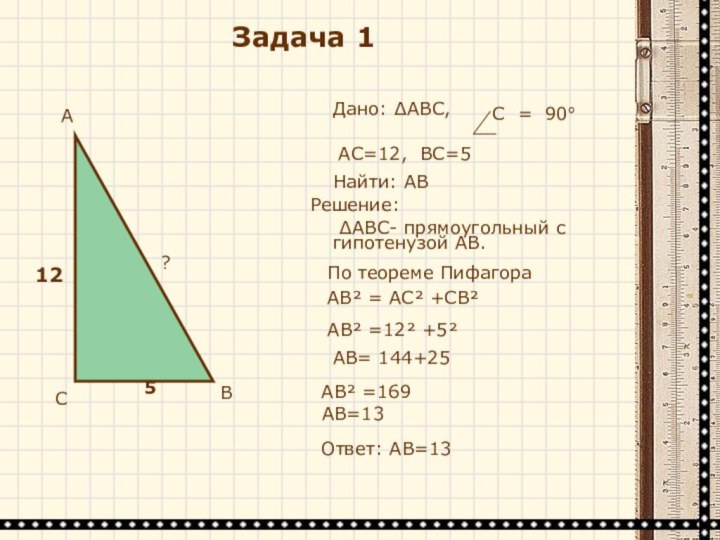
Дано: ∆АВС,
∆АВС- прямоугольный с
гипотенузой АВ.
По теореме Пифагора
АВ² = АС² +СВ²
АВ² =12²
+5²АВ² =169
АВ=13
AC=12, BC=5
Найти: АВ
Решение:
АВ= 144+25
Ответ: АВ=13
Задача 1
Слайд 25
с² = а2 + b2
с=13
а=12
13² = 122 +b2
169
= 144 + b2
b2 =169-144
b² = 25
b=5
Задача 2
Найти b
Решение:
Слайд 31
Задача из китайской
"Математики в девяти книгах"
"Имеется водоем
со стороной в 1 чжан = 10 чи. В
центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.Спрашивается: какова глубина воды и какова длина камыша?"
ИСТОРИЧЕСКИЕ ЗАДАЧИ
Слайд 32
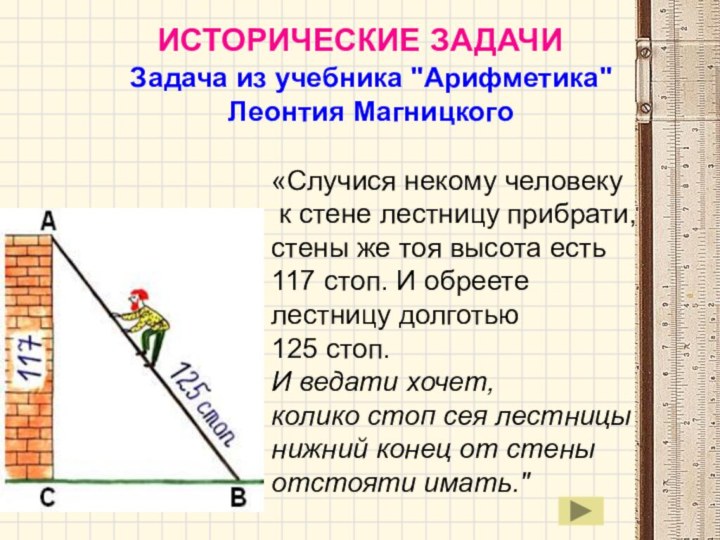
Задача из учебника "Арифметика"
Леонтия Магницкого
«Случися некому человеку
к стене лестницу прибрати, стены же тоя высота есть
117 стоп. И обреете
лестницу долготью
125 стоп.
И ведати хочет,
колико стоп сея лестницы нижний конец от стены отстояти имать."
ИСТОРИЧЕСКИЕ ЗАДАЧИ