Презентация на тему Представление о правильных многогранниках

скромный по численности отряд сумел пробраться в самые глубины

различных наук»
Л. Кэрролл

тетраэдр, куб, октаэдр, додекаэдр, икосаэдр

указывается число граней:
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«додека»

− 12;
«икоса» − 20;
«эдра» − грань.

Презентация 1

числу рёбер, увеличенному на 2.
Г + В =

Р + 2

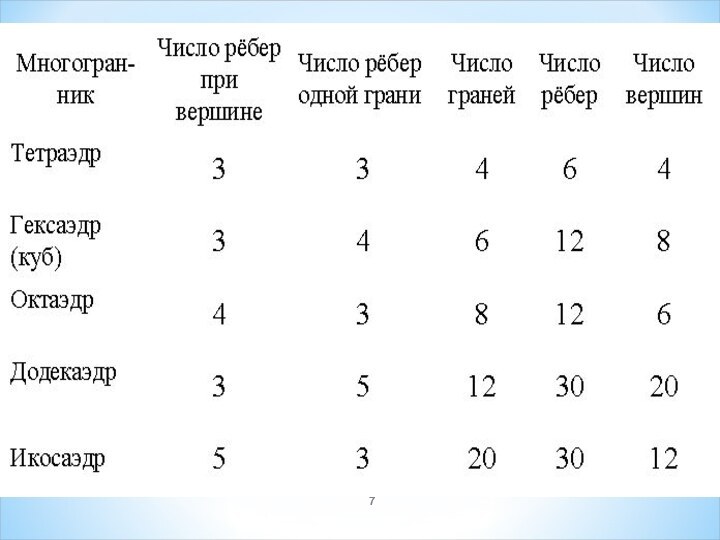
Формула Эйлера

Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г + В − Р = 2

icosahtdra) по форме напоминает икосаэдр.

Феодария
(Circjgjnia icosahtdra)

Презентация 2

Платоновыми телами, поскольку они занимают видное место в философской

картине мира, разработанной великим мыслителем Древней Греции Платоном.
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

Правильные многогранники в философской картине мира Платона

Платон
(ок. 428 - ок. 348 до н.э.)

сферу орбиты Сатурна можно вписать куб, в который вписывается

сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия.
Такая модель Солнечной системы получила название «Космического кубка» Кеплера.

«Космический кубок» Кеплера

Модель Солнечной
системы
И. Кеплера

свойства растущего кристалла, оказывающего воздействие на развитие всех природных

процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.

Икосаэдро-
додекаэдровая
структура Земли

Икосаэдро-додекаэдровая
структура Земли

человек, а их создала природа в виде кристаллов и

снежинок;
что модели многогранников можно изготовить из разверток.