раздел математики, изучающий тригонометрические функции. Сложно представить, но с
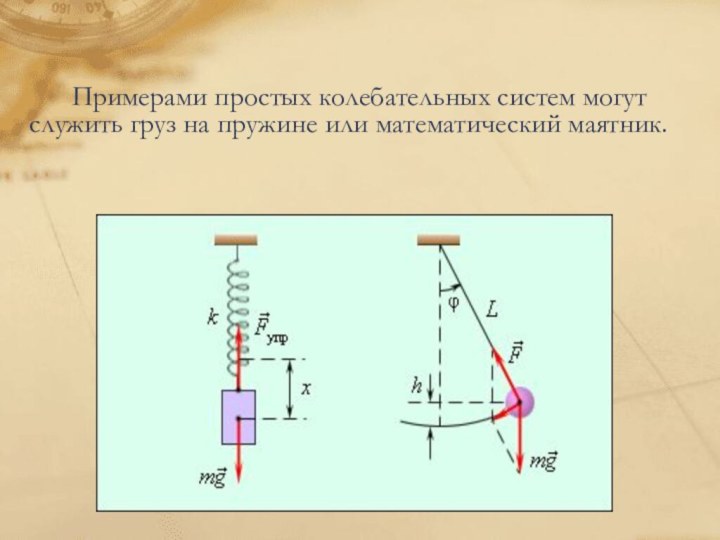
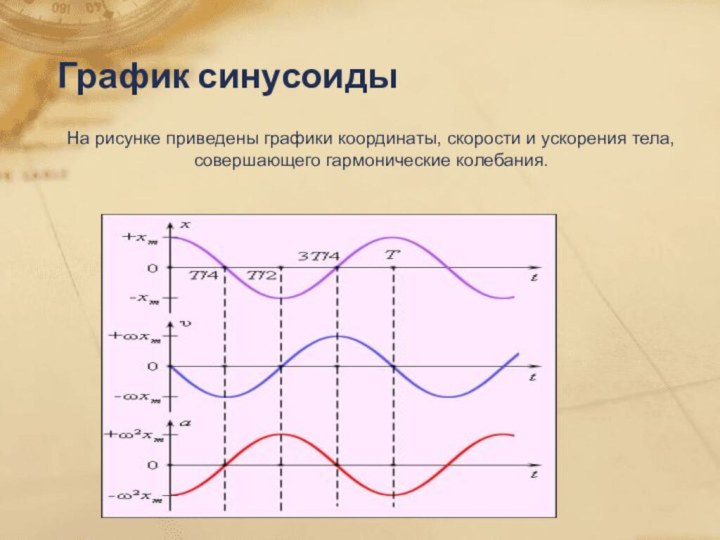
этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Вы могли не подозревать об этом, но тригонометрия встречается в таких науках, как физика, биология, не последнюю роль она играет и в медицине, и, что самое интересное, без нее не обошлось даже в музыке и архитектуре.Введение









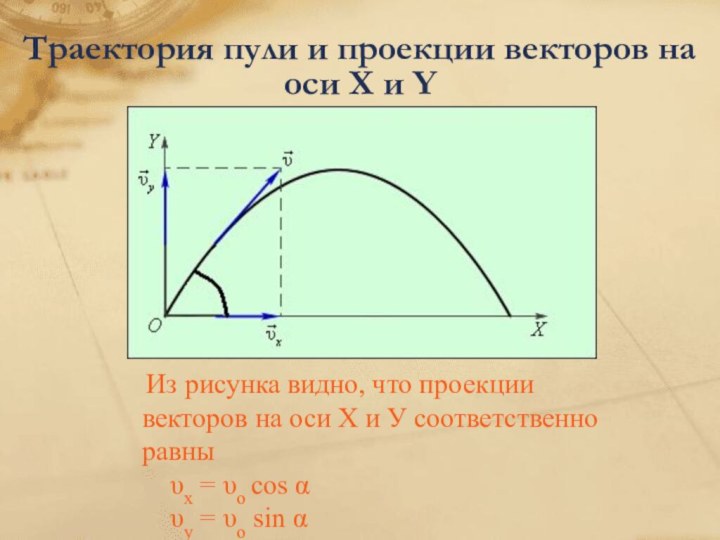

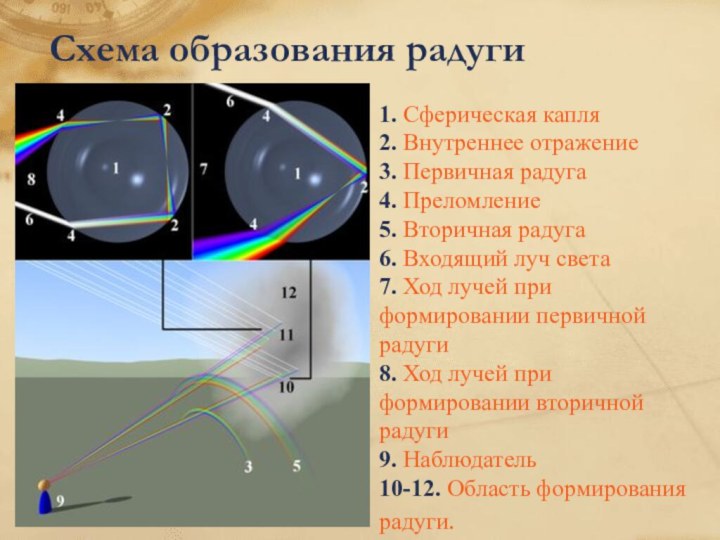








![Презентация Тригонометрия в окружающем нас мире Феликс Кандела Ресторан в Лос-Манантиалесе[adcos(t) + ddt , bdsin(t), cdt + edt2]](/img/tmb/7/660544/cc683f7c4a10abe44fd1adad0568e362-720x.jpg)