Презентация на тему по геометрии на тему Некоторые свойства окружности. Касательная к окружности

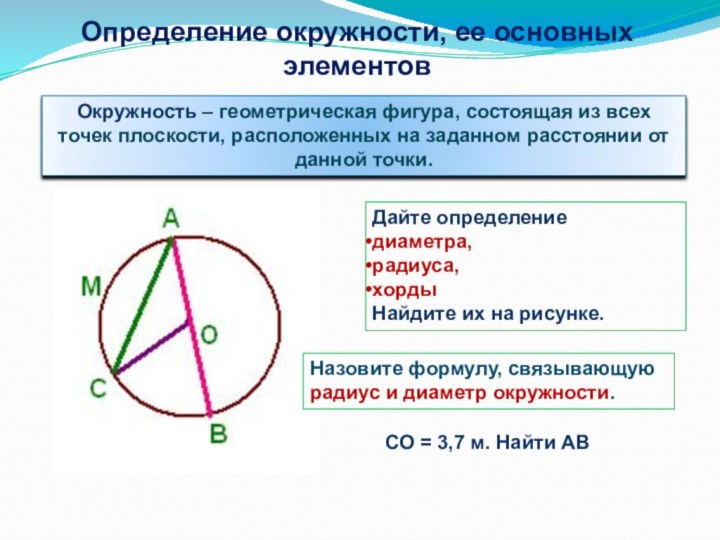
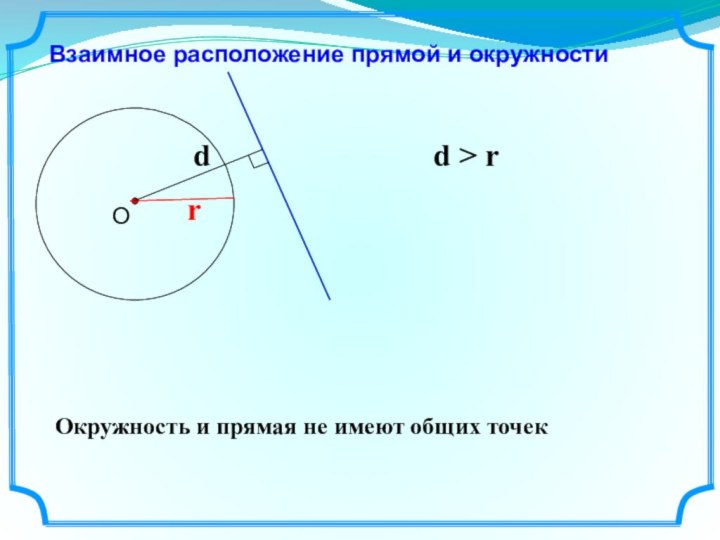
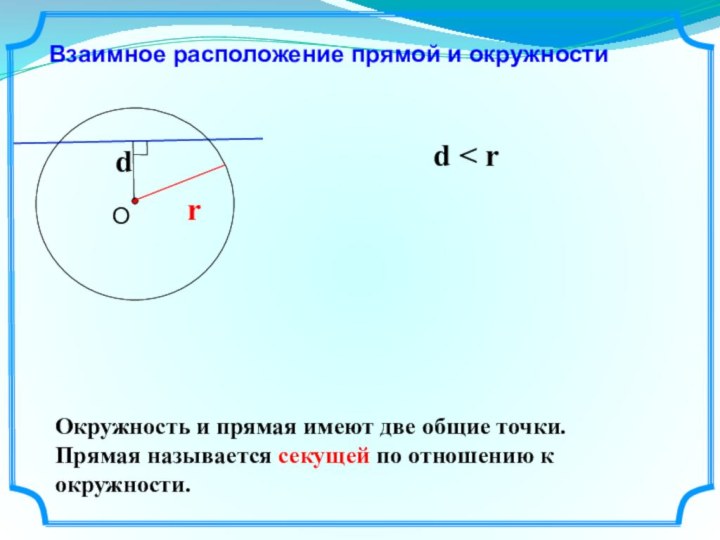
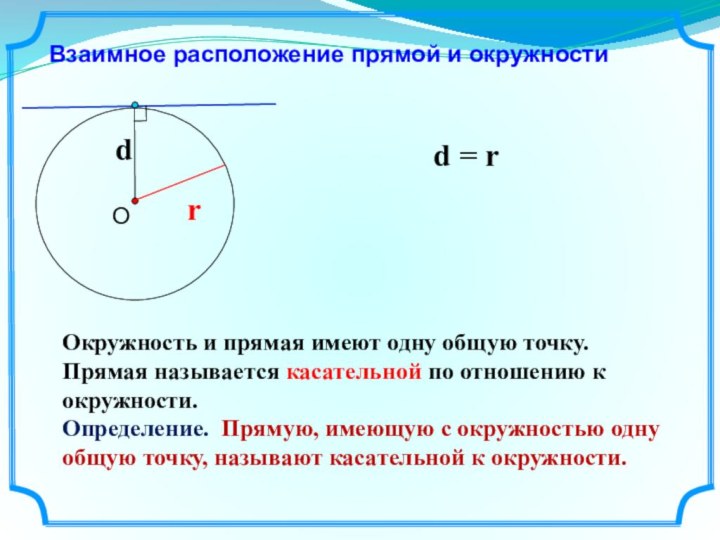
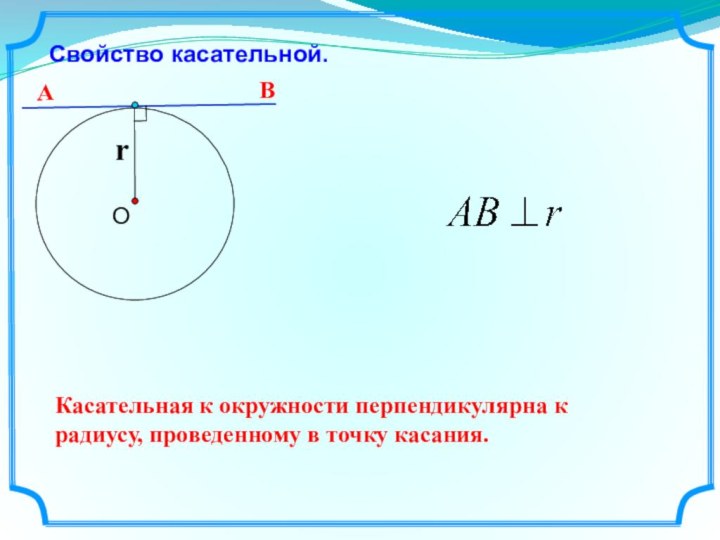
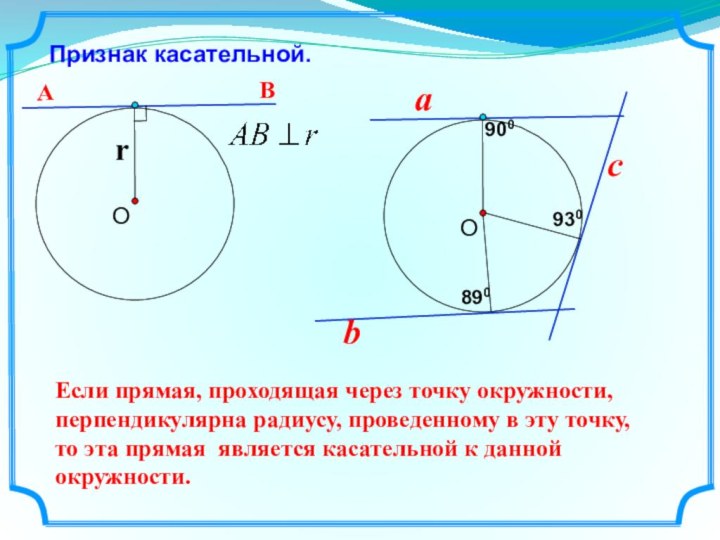
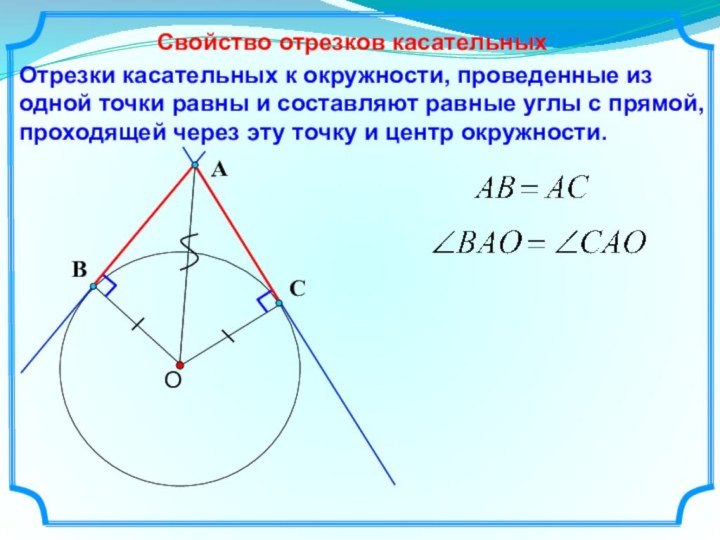
плоскости, расположенных на заданном расстоянии от данной точки.
Определение окружности,

Дайте определение
диаметра,
радиуса,
хорды
Найдите их на рисунке.

Назовите формулу, связывающую радиус и диаметр окружности.

СО = 3,7 м. Найти АВ

пополам.
Дано: окружность,
 
Доказать: М – середина АВ
Доказательство:
1. Проведем радиусы

2. Треугольник АОВ равнобедренный.

3. ОМ – высота проведенная к основанию, ОМ – медиана.

Обратная теорема.
Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.

прямая не имеют общих точек

прямая имеют две общие точки.
Прямая называется секущей по отношению

прямая имеют одну общую точку.
Прямая называется касательной по отношению

в точку касания.

А
В

радиусу, проведенному в эту точку, то эта прямая является