- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Правильные многоугольники (9 класс)
Содержание
- 2. Выпуклый многоугольникМногоугольник называется выпуклым, если он лежит
- 3. Правильный многоугольникПравильный треугольникКвадратПравильный пятиугольникПравильный шестиугольникПравильным многоугольником называется
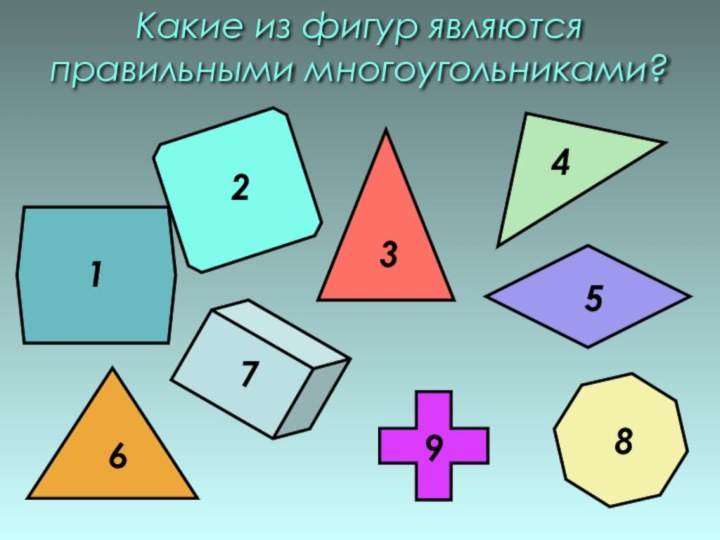
- 4. Какие из фигур являются правильными многоугольниками?
- 5. Сумма углов выпуклого n – угольника
- 6. Вписанная окружность Если все стороны многоугольника касаются
- 7. Описанная окружность Если все вершины многоугольника лежат
- 8. Теорема об окружности, описанной около правильного многоугольникаА1Аn
- 9. Теорема об окружности, вписанной в правильный многоугольникА2А1Аn
- 10. ОRrСледствие 2 Центр окружности описаннойоколо правильногомногоугольника, совпадает
- 11. Скачать презентацию
- 12. Похожие презентации
Выпуклый многоугольникМногоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.






Слайд 3
Правильный многоугольник
Правильный
треугольник
Квадрат
Правильный
пятиугольник
Правильный
шестиугольник
Правильным многоугольником называется выпуклый
многоугольник, у которого все углы равны и все стороны
равны.
Слайд 5
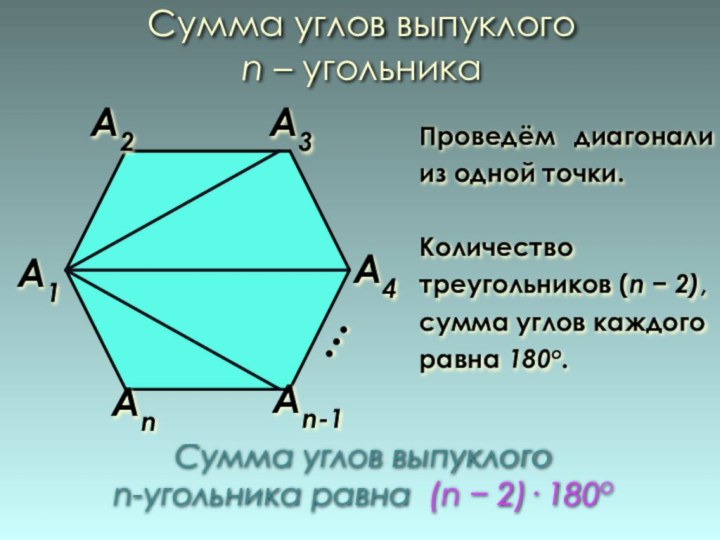
Сумма углов выпуклого
n – угольника
А1
Аn
А4
А3
А2
Проведём диагонали
из одной точки.
Количество треугольников (n − 2), сумма углов
каждого равна 180о. Сумма углов выпуклого
n-угольника равна (n − 2)· 180о
Аn-1
…
Слайд 6
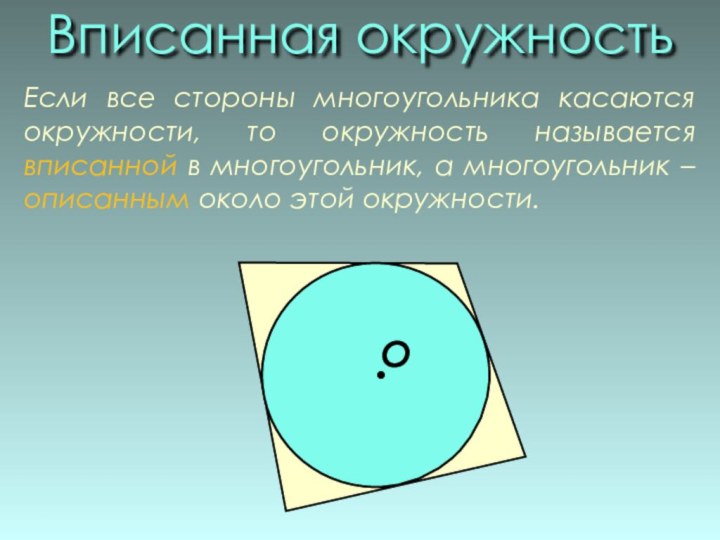
Вписанная окружность
Если все стороны многоугольника касаются окружности,
то окружность называется вписанной в многоугольник, а многоугольник –
описанным около этой окружности.О
Слайд 7
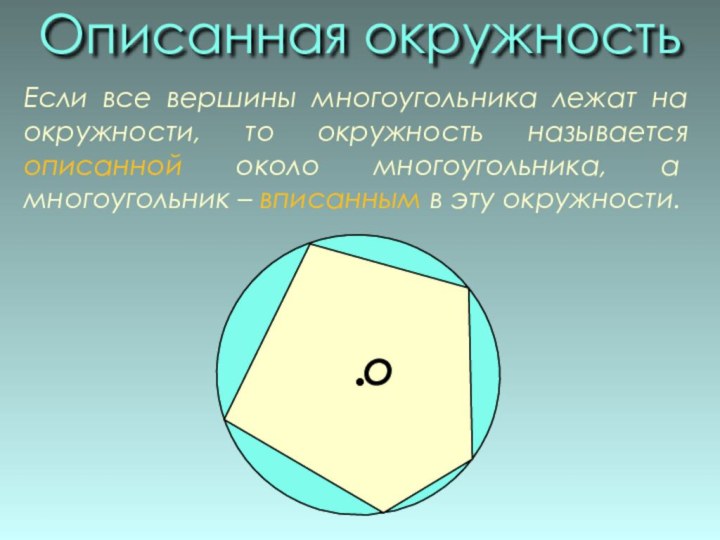
Описанная окружность
Если все вершины многоугольника лежат на
окружности, то окружность называется описанной около многоугольника, а многоугольник
– вписанным в эту окружности.О
Слайд 8
Теорема об окружности, описанной около правильного многоугольника
А1
Аn -1
А3
А2
Аn
…
А4
Дано:
А1А2А3…Аn – правильный n-угольник
Доказать: около А1А2А3…Аn можно описать окружность;
она – единственнаяОколо любого правильного многоугольника можно описать окружность, и притом только одну.
О
Слайд 9
Теорема об окружности, вписанной в правильный многоугольник
А2
А1
Аn -1
А3
Аn
…
А4
В
любой правильный многоугольник можно вписать окружность, и притом только
одну.Дано: А1А2А3…Аn – правильный n-угольник
Доказать: в А1А2А3…Аn можно вписать окружность;
она – единственная
О
Слайд 10
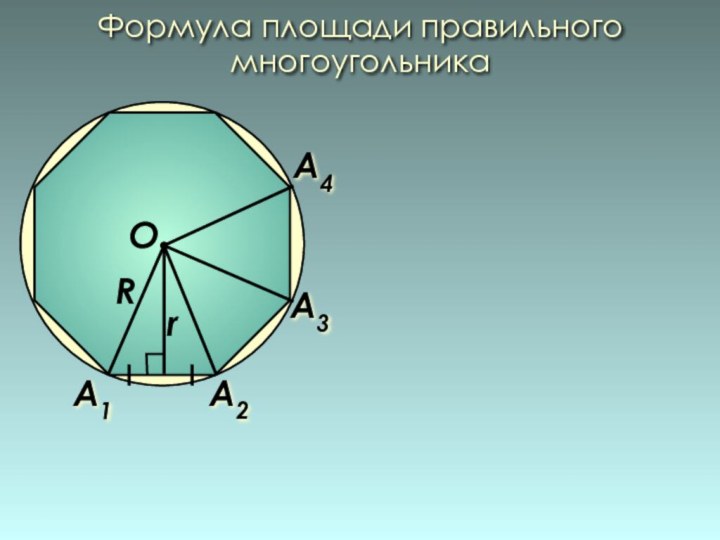
О
R
r
Следствие 2
Центр окружности описанной
около правильного
многоугольника, совпадает с
центром окружности
вписанной в тот же
многоугольник.
Следствие1
Окружность, вписанная в правильный
многоугольник,
касается сторон
многоугольника
в их серединах.О – центр правильного многоугольника





























