- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Теорема Пифагора
Содержание
- 2. Пифагор Самосский - древнегреческий философ, математик, мистик, создатель
- 3. Теорема Пифагора В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
- 4. Способы доказательства теоремы ПифагораСпособ 1CH-высотаКатет прямоугольного треугольника
- 5. Способ 3Рассмотрим прямоугольный треугольник с катетами а, в и
- 6. Способ 4Для доказательства на катете ВС строим Δ BCD ABC (Мы знаем,
- 7. Скачать презентацию
- 8. Похожие презентации
Пифагор Самосский - древнегреческий философ, математик, мистик, создатель религиозно-философской школы пифагорейцев. Одним из главных достижений Пифагора считается открытие Теоремы, которая в последствии стала носить его имя.






Слайд 2 Пифагор Самосский - древнегреческий философ, математик, мистик, создатель религиозно-философской
школы пифагорейцев.
которая в последствии стала носить его имя.
Слайд 3
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы
равен сумме квадратов длин катетов
Слайд 4
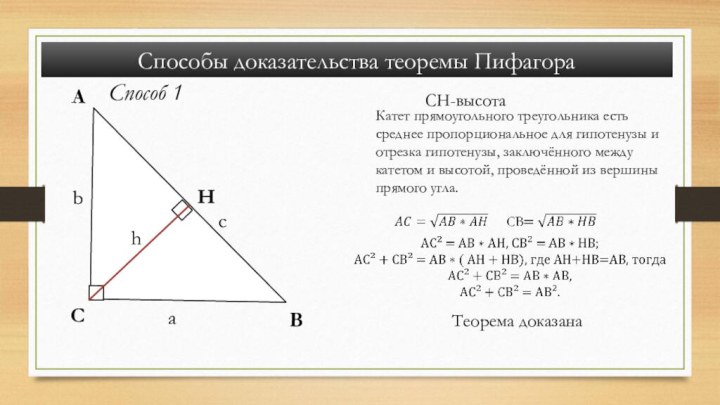
Способы доказательства теоремы Пифагора
Способ 1
CH-высота
Катет прямоугольного треугольника есть
среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между
катетом и высотой, проведённой из вершины прямого угла.Теорема доказана
H
h
c
Слайд 5
Способ 3
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с (рис.1).
Докажем,
что с²=а²+в².
Доказательство.
Достроим треугольник до квадрата со стороной а + в так, как
показано на рис. 2. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².Таким образом,
(а + в)² = 2ав + с²,
откуда
с²=а²+в².
Теорема доказана.
Слайд 6
Способ 4
Для доказательства на катете ВС строим Δ BCD ABC (Мы знаем, что
площади подобных фигур относятся как квадраты их сходственных линейных
размеров: Вычитая из первого равенства второе, получимДоказательство закончено.