Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Касательная к окружности

Содержание

Математический диктант
Касательная к окружностиУчитель математики ГБОУ Гимназии №1592Крайнюк А.Л. Математический диктант Определение: прямая, имеющая с окружностью только одну общую точку, называется касательной к Свойство касательной:Касательная к окружности перпендикулярна к радиусу, проведенному в точку касанияpА pАДано:Окр(О;r),Р – касательнаяДоказать: р┴ ОАДоказательство:Допустим, что прямая р не перпендикулярна радиусу. Тогда:К АBCОтрезки АВ и АС - отрезки касательных, проведенных из точки А1234 Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные pАДано:Окр(О;ОА),ОА┴рДоказать: р – касательнаяЕСЛИ ПРЯМАЯ ПРОХОДИТ ЧЕРЕЗ КОНЕЦ РАДИУСА, ЛЕЖАЩЕГО НА ОКРУЖНОСТИ, UROKIMATEMATIKI.RUИгорь Жаборовский © 2012АЗадача 1: через данную точку А окружности с центром Задача 2: Дан прямоугольник АВСD, где АВ = 8см, а Задача 3: Прямая АВ – касательная в точке А к окружности с Задача 4: Прямые АВ и АС касаются окружности с центром в т Домашнее задание:П.69 №634, №636, №639
Слайды презентации

Слайд 2 Математический диктант

Математический диктант

Слайд 3 Определение: прямая,
имеющая с окружностью
только одну общую

Определение: прямая, имеющая с окружностью только одну общую точку, называется касательной

точку,
называется касательной к
окружности, а их общая
точка

– точкой касания
прямой и окружности.

Слайд 4 Свойство касательной:
Касательная к окружности
перпендикулярна к
радиусу, проведенному

Свойство касательной:Касательная к окружности перпендикулярна к радиусу, проведенному в точку касанияpА

в
точку касания
p
А

Слайд 5 p
А
Дано:
Окр(О;r),
Р – касательная

Доказать: р┴ ОА
Доказательство:
Допустим, что прямая р

pАДано:Окр(О;r),Р – касательнаяДоказать: р┴ ОАДоказательство:Допустим, что прямая р не перпендикулярна радиусу. Тогда:К

не перпендикулярна радиусу. Тогда:
К

Слайд 6 А
B
C
Отрезки АВ и АС - отрезки касательных, проведенных

АBCОтрезки АВ и АС - отрезки касательных, проведенных из точки А1234

из точки А
1
2
3
4

Слайд 7 Отрезки касательных к
окружности,
проведенные из одной
точки

Отрезки касательных к окружности, проведенные из одной точки равны и составляют

равны и
составляют равные углы
с прямой, проходящей
через

эту точку и центр
окружности

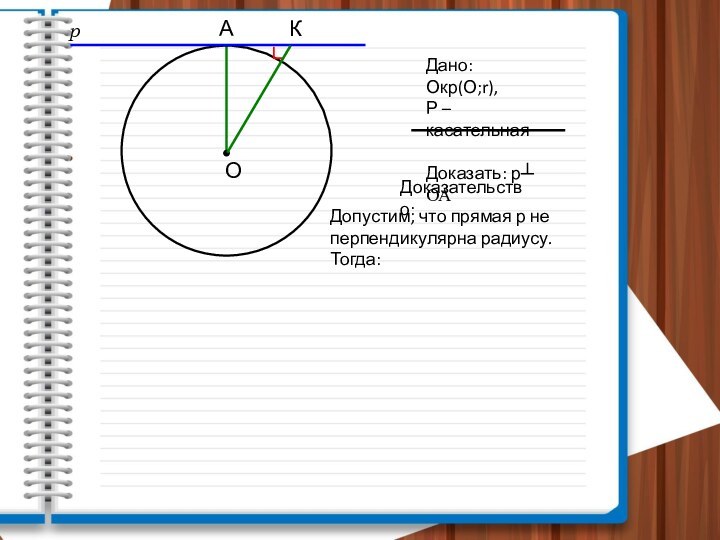
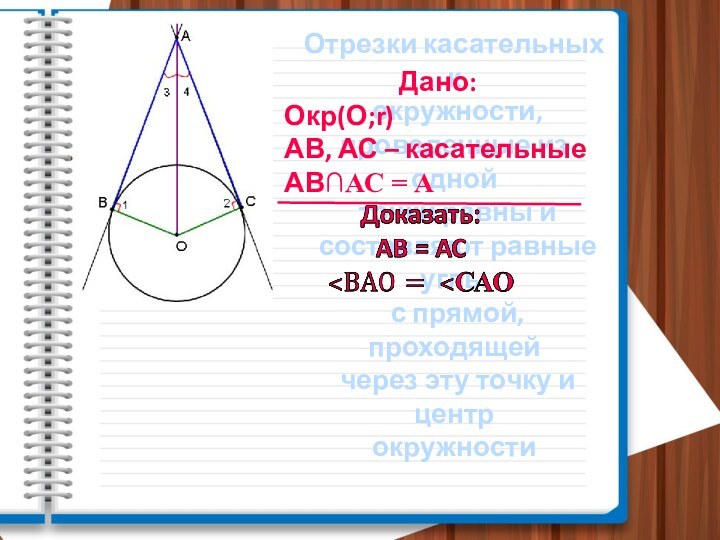
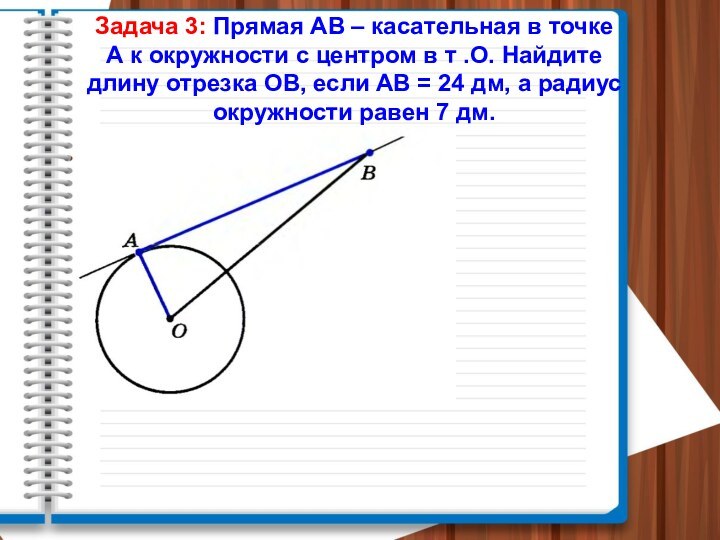
Дано:
Окр(О;r)
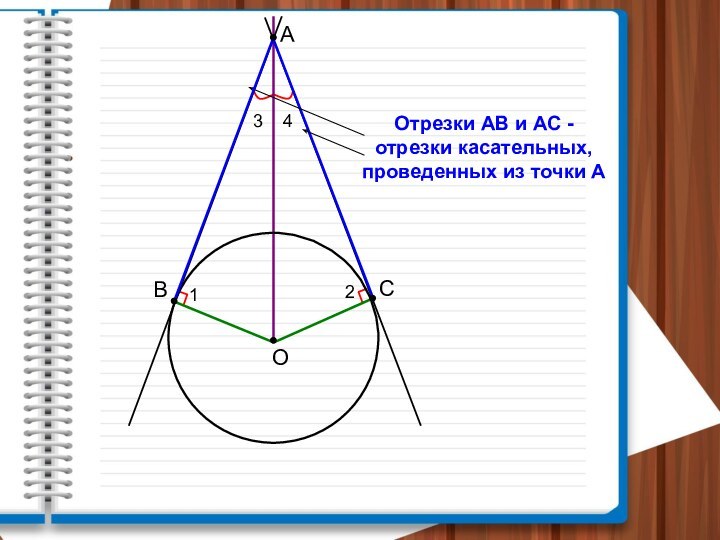
АВ, АС – касательные
АВ∩АС = А

Слайд 8 p
А
Дано:
Окр(О;ОА),
ОА┴р

Доказать: р – касательная
ЕСЛИ ПРЯМАЯ ПРОХОДИТ ЧЕРЕЗ КОНЕЦ

pАДано:Окр(О;ОА),ОА┴рДоказать: р – касательнаяЕСЛИ ПРЯМАЯ ПРОХОДИТ ЧЕРЕЗ КОНЕЦ РАДИУСА, ЛЕЖАЩЕГО НА

РАДИУСА, ЛЕЖАЩЕГО НА ОКРУЖНОСТИ, И ПЕРПЕНДИКУЛЯРНА К ЭТОМУ РАДИУСУ,

ТО ОНА ЯВЛЯЕТСЯ КАСАТЕЛЬНОЙ

Слайд 9 UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
А
Задача 1: через данную точку

UROKIMATEMATIKI.RUИгорь Жаборовский © 2012АЗадача 1: через данную точку А окружности с

А окружности с центром О провести касательную к этой

окружности

p

Слайд 10 Задача 2: Дан прямоугольник АВСD, где

Задача 2: Дан прямоугольник АВСD, где АВ = 8см, а

АВ = 8см, а ВС = 6 см. Какие

из прямых АС, ВС, CD и BD являются секущими по отношению к окружности с центром в т. А радиуса 6 см.

А

В

С

D

Слайд 11 Задача 3: Прямая АВ – касательная в точке

Задача 3: Прямая АВ – касательная в точке А к окружности

А к окружности с центром в т .О. Найдите

длину отрезка ОВ, если АВ = 24 дм, а радиус окружности равен 7 дм.

Слайд 12 Задача 4: Прямые АВ и АС касаются окружности

Задача 4: Прямые АВ и АС касаются окружности с центром в

с центром в т .О в т. В и

С. Найдите угол ОАВ, если АВ = ВС.
  • Имя файла: kasatelnaya-k-okruzhnosti.pptx
  • Количество просмотров: 196
  • Количество скачиваний: 0
- Предыдущая КРОШ И ЕЖИК НА РЫБАЛКЕ
Следующая - Экологические проблемы Пермского края

Похожие презентации

Презентация по геометрии к уроку Сумма углов треугольника 7класс Презентация по геометрии к уроку Сумма углов треугольника 7класс 157
Презентация по математике на тему Многогранники10 класс Презентация по математике на тему Многогранники10 класс 136
Презентация по геометрии на тему Построение биссектрисы угла (7 класс) Презентация по геометрии на тему Построение биссектрисы угла (7 класс) 175
Зачем нужна геометрия Зачем нужна геометрия 282
Сечение призмы Сечение призмы 172
Геометрия в природе Геометрия в природе 244
Детская презентация по математике Симметрия в архитектуре Детская презентация по математике Симметрия в архитектуре 191
Презентация по математике на тему : Круги Эйлера. Презентация по математике на тему : Круги Эйлера. 208
Параллельные и перпендикулярные прямые Параллельные и перпендикулярные прямые 331
Компланарные векторы Компланарные векторы 144
Презентация Формула Пика по нахождению площади фигуры Презентация Формула Пика по нахождению площади фигуры 200
Перпендикулярные прямые в пространстве Перпендикулярные прямые в пространстве 164
Смежные и вертикальные углы Смежные и вертикальные углы 164
Определение многоугольника Определение многоугольника 172
Шар 11 класс Шар 11 класс 128
Признаки равенства и подобия треугольников Признаки равенства и подобия треугольников 142
Презентация по геометрии на тему Призма (10 класс) Презентация по геометрии на тему Призма (10 класс) 159
Презентация по теме Определение подобных треугольников Презентация по теме Определение подобных треугольников 163
Перпендикулярные прямые 6 класс Перпендикулярные прямые 6 класс 203
Евклид Евклид 210
Параллель түзулер. Геометрия 7 - сынып Параллель түзулер. Геометрия 7 - сынып 366
Касательная. Уравнение касательной Касательная. Уравнение касательной 172
Бинарный урок геометрии и информатики Четырехугольники. Решение задач Лауреат Бинарный урок геометрии и информатики Четырехугольники. Решение задач Лауреат 161
Презентация по математике Решение задач на нахождение площадей при подготовке к ЕГЭ Презентация по математике Решение задач на нахождение площадей при подготовке к ЕГЭ 172
Перпендикуляр и наклонная Перпендикуляр и наклонная 160
Египетские пирамиды Египетские пирамиды 188
Как найти площадь прямоугольника? Как найти площадь прямоугольника? 136
Презентация по геометрии Задачи на построение Презентация по геометрии Задачи на построение 170
Презентация по геометрии на тему Сумма углов треугольника(7 класс) Презентация по геометрии на тему Сумма углов треугольника(7 класс) 154
ЭОР по геометрии на тему Признаки равенства треугольников (7 класс) ЭОР по геометрии на тему Признаки равенства треугольников (7 класс) 206