- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
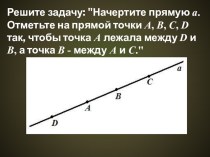
Презентация на тему Учебная презентация по теме Аксиома параллельных прямых
Содержание
- 2. Аксиома параллельных прямых*Автор презентации: Лавлинский Максим Викторович
- 3. Цели урока:1. Узнать, что такое аксиома2. Рассмотреть аксиому параллельных прямых и ее следствия.
- 4. Дать определение параллельных прямыхДве прямые на плоскости называются параллельными, если они не пересекаютсяaba||b
- 5. Назвать все углы при пересечении двух прямых
- 6. Сформулировать признаки параллельности двух прямых 1.
- 7. Сформулировать признаки параллельности двух прямых 2.
- 8. Сформулировать признаки параллельности двух прямых 3.
- 9. Решить задачуabc12435687Дано: c ∩ a, c
- 10. Практические способы построения параллельных прямыхaMb
- 11. Мы можем решить такую задачу: через точку,
- 12. aMbМожно ли через т. М провести еще
- 13. aMbb´ Называли эту проблему проблемой пятого постулата,
- 14. aMbb´ И только наш русский ученый Н.И.
- 15. В геометрии слово «аксиома» вы слышите впервые,
- 16. Теорема Теорема
- 17. Сначала формулируются исходные положения - аксиомыНа их
- 18. На самом деле, с аксиомами вы уже встречались в I главе и во II главе
- 19. Например, аксиомой является утверждение о том, что
- 20. Сравнение двух отрезков вы проводили с помощью
- 21. Сравнение двух углов основано на аналогичной аксиоме:
- 22. Обо всех аксиомах планиметрии вы можете прочитать в конце учебника в приложении 1.
- 23. Аксиома параллельных прямых:Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- 24. У этой аксиомы есть следствия 1о и
- 25. 1. Если прямая пересекает одну
- 26. Цель последующих уроков – научиться использовать аксиому
- 27. Домашнее задание:1. П. 27, 28, 2. № 196, 198
- 28. Тест:
- 29. Решение задачЗадача №1 Через точку,
- 30. Скачать презентацию
- 31. Похожие презентации




























Слайд 3
Цели урока:
1. Узнать, что такое аксиома
2. Рассмотреть аксиому
параллельных прямых и ее следствия.
Слайд 4
Дать определение параллельных прямых
Две прямые на плоскости
называются параллельными, если они не пересекаются
a
b
a||b
Слайд 5
Назвать все углы при пересечении двух прямых секущей
a
b
c
1
2
4
3
5
6
8
7
∠3
и ∠5, ∠4 и ∠6
∠4 и ∠5, ∠3 и
∠6∠1 и ∠5, ∠4 и ∠8,
∠2 и ∠6, ∠3 и ∠7,
Накрест лежащие углы
Односторонние углы
Соответственные углы
Слайд 6
Сформулировать признаки параллельности двух прямых
1. Если
при пересечении двух прямых секущей накрест лежащие углы равны,
то прямые параллельныa
b
c
1
2
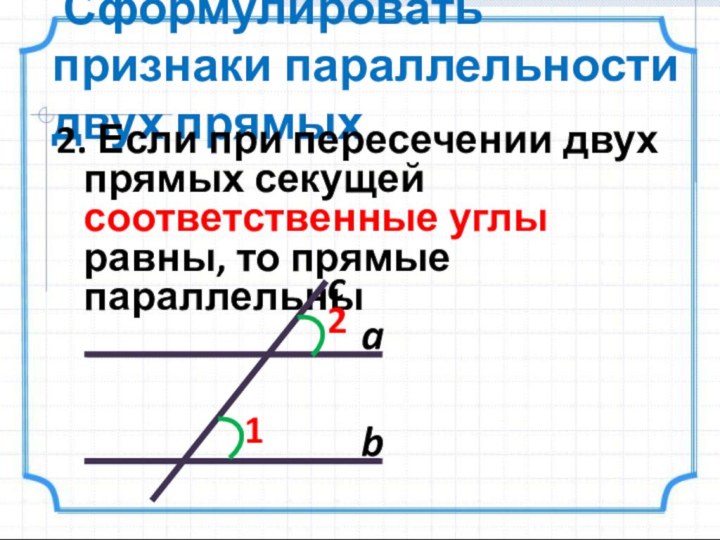
Слайд 7
Сформулировать признаки параллельности двух прямых
2. Если
при пересечении двух прямых секущей соответственные углы равны, то
прямые параллельныa
b
c
1
2
Слайд 8
Сформулировать признаки параллельности двух прямых
3. Если
при пересечении двух прямых секущей сумма односторонних углов равна
180°, то прямые параллельныa
b
c
1
2
∠1+∠2=180°
Слайд 9
Решить задачу
a
b
c
1
2
4
3
5
6
8
7
Дано: c ∩ a, c ∩
b,
1=30° ,
∠ 6 в 5 раз больше ∠1
Доказать:
а||bРешите задачу тремя способами:
30°
150°
Слайд 11 Мы можем решить такую задачу: через точку, не
лежащую на прямой, провести прямую, параллельную данной.
А сколько таких
прямых можно провести?
Слайд 12
a
M
b
Можно ли через т. М провести еще одну
прямую , параллельную прямой а ?
Нам представляется, что
через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.Можно ли это утверждение доказать?
Может, существует еще одна прямая b´, проходящая через т. М и параллельная прямой а?
b´
Слайд 13
a
M
b
b´
Называли эту проблему проблемой пятого постулата, потому
что в геометрии Евклида это утверждение называлось пятым постулатом,
а Евклид жил в III веке до нашей эры.Оказывается, доказать это невозможно, хотя ученые на протяжении многих веков пытались это сделать.
Слайд 14
a
M
b
b´
И только наш русский ученый Н.И. Лобачевский,
обосновал, что это утверждение не может быть доказано.
Значит утверждение,
что через т. М нельзя провести прямую (отличную от прямой в), параллельную прямой а - это аксиома. Слайд 15 В геометрии слово «аксиома» вы слышите впервые, но
в жизни оно часто употребляется.
Какое у него значение?
Слайд 16
Теорема
Теорема
Теорема
ТеоремаОб аксиомах геометрии
А на чём основаны доказательства самых первых теорем геометрии?
На аксиомах
Утверждениях о свойствах геометрических фигур, которые принимаются в качестве исходных положений ( без доказательства)
?
Строится вся геометрия
Слайд 17
Сначала формулируются исходные положения - аксиомы
На их основе,
путём логических рассуждений доказываются другие утверждения
Такой подход к
построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
Слайд 19 Например, аксиомой является утверждение о том, что через
любые две точки проходит прямая, и притом только одна.
А
В
Слайд 20 Сравнение двух отрезков вы проводили с помощью наложения
одного отрезка на другой. Возможность такого наложение вытекает из
следующей аксиомы: на любом луче от его начала можно отложить отрезок, равный данному, и притом только один. AB=CD
Слайд 21 Сравнение двух углов основано на аналогичной аксиоме: от
любого луча в заданную сторону можно отложить угол, равный
данному неразвернутому углу, и притом только один
Слайд 23
Аксиома параллельных прямых:
Через точку, не лежащую на данной
прямой, проходит только одна прямая, параллельная данной.
Слайд 24
У этой аксиомы есть следствия 1о и 2о.
Утверждения,
которые выводятся непосредственно из аксиом или теорем, называются следствиями.
Слайд 25 1. Если прямая пересекает одну из
двух параллельных прямых, то она пересекает и другую.
2.Если две прямые параллельны третьей прямой, то они параллельны.
Следствия из аксиомы параллельных прямых
а
в
М
с
Доказательство:
Предположим, что прямая с не пересекает прямую в, значит, с ⎪⎪в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
а
в
с
Доказательство:
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.
Способ рассуждения, который называется методом доказательства от противного
Слайд 26 Цель последующих уроков – научиться использовать аксиому параллельных
прямых при изучении свойств прямых и при решении задач.
Слайд 29
Решение задач
Задача №1
Через точку, не
лежащую на данной прямой p , проведены четыре прямые.
Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи.А
р
Задача №2
Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АВ и ВС пересекают прямую р.
А
В
С
р