Презентация на тему по геометрии тема Треугольники (подготовка к ОГЭ 9 класс)

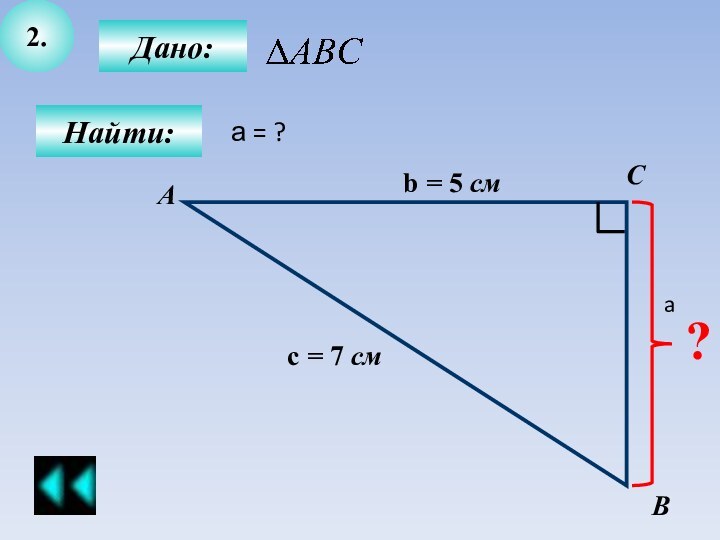
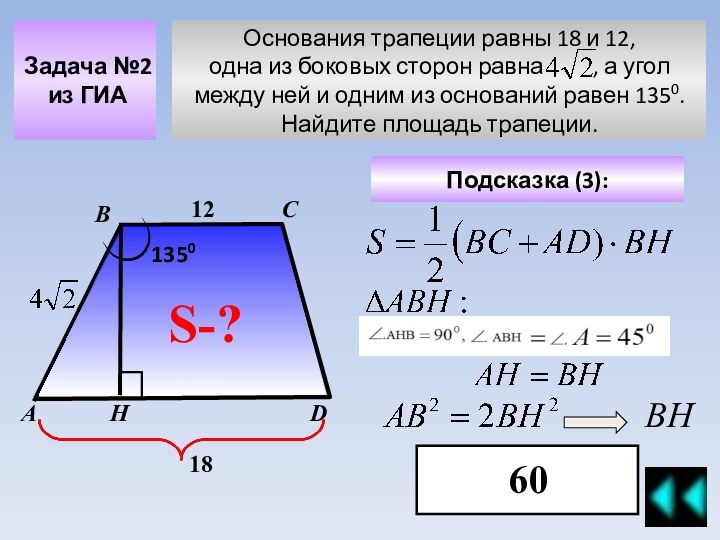
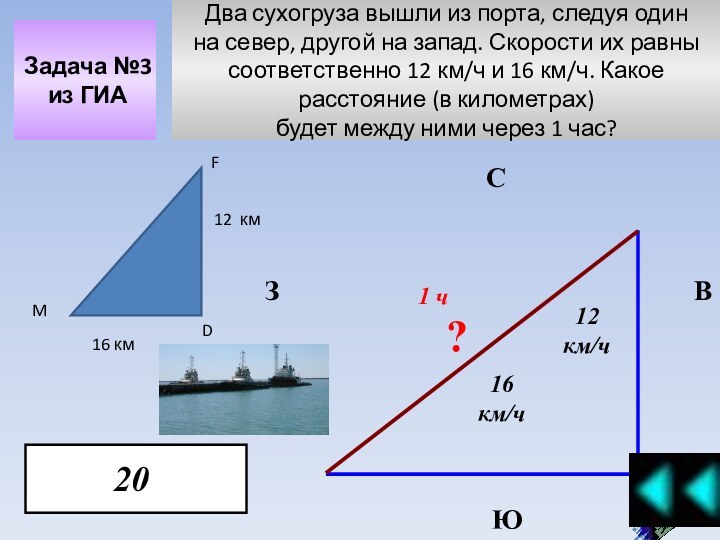
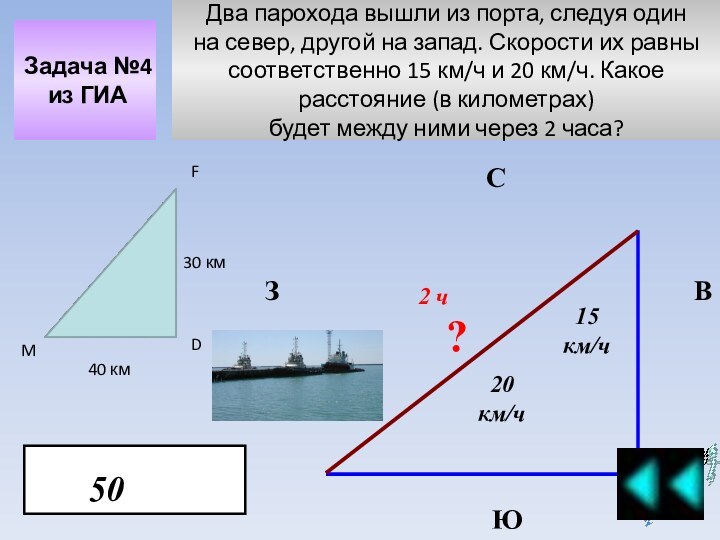
ОГЭ в 9 классе по математике разделен на 3

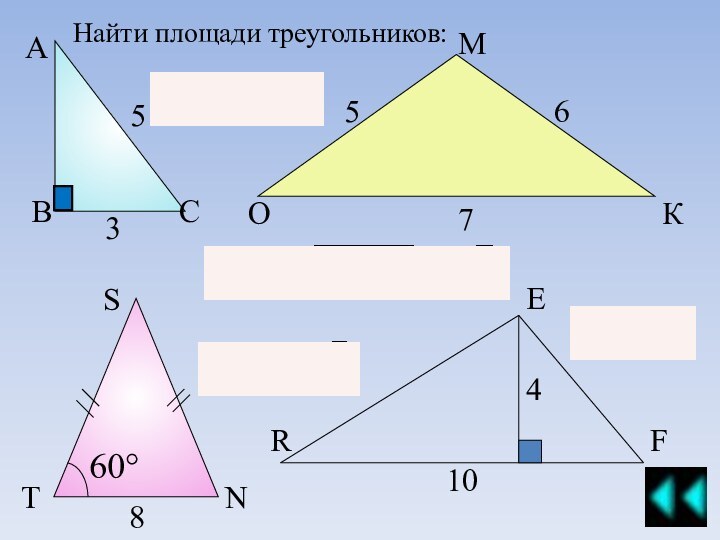
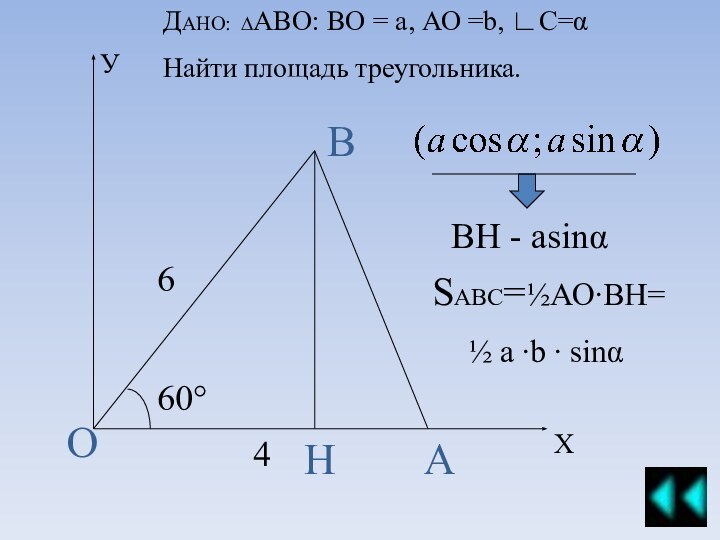
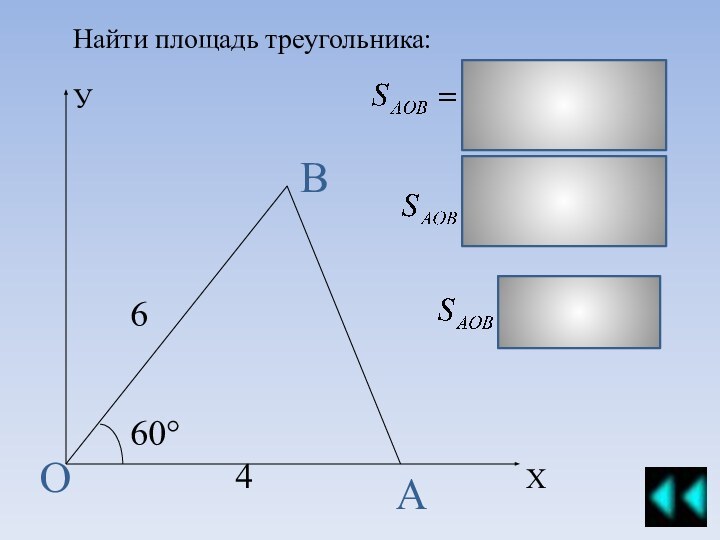
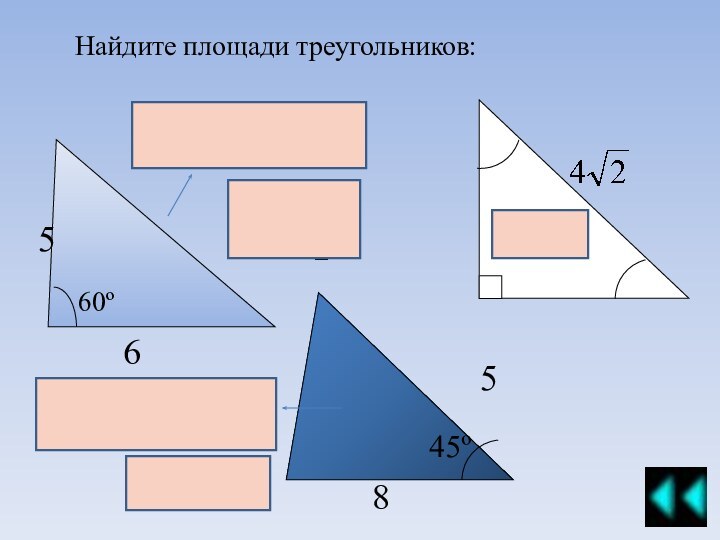
модуля: алгебра, геометрия и реальная математика. В модуль геометрия входят различные задания, при выполнении которых необходимы знания и умения решать задачи по темам, связанным с такой фигурой, как треугольник.
Вы имеете возможность самостоятельно повторить и прорешать задачи по этой теме. Предложенный квест – это самоучитель, который снабжен необходимым справочным материалом для решения задач.
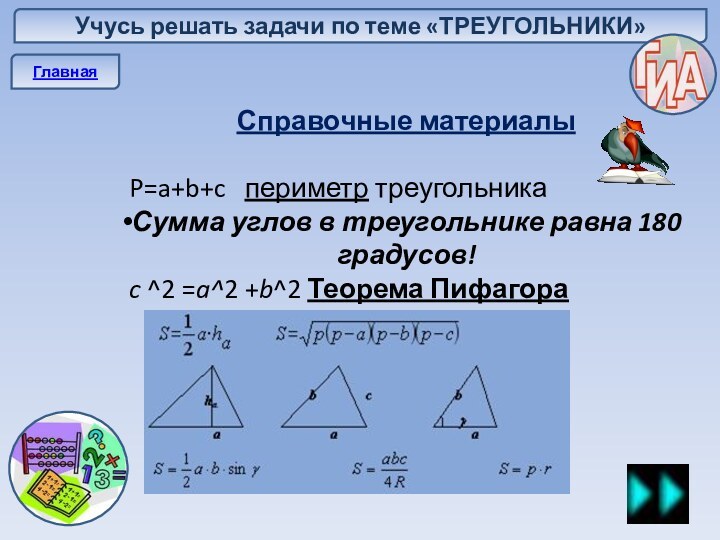
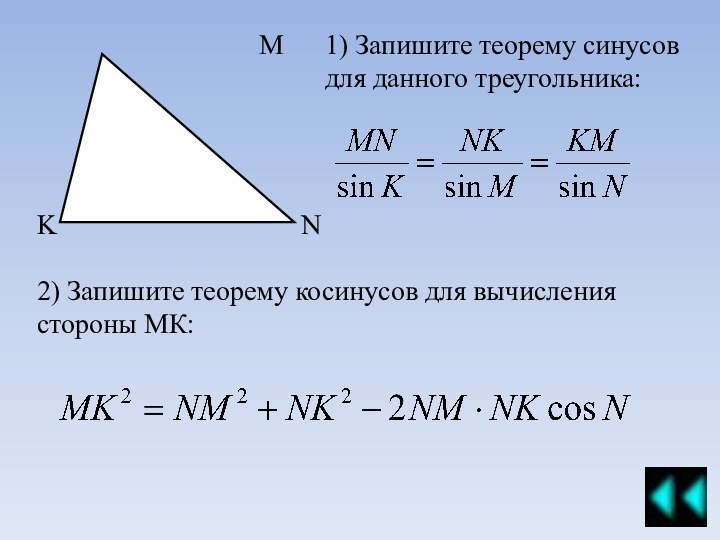
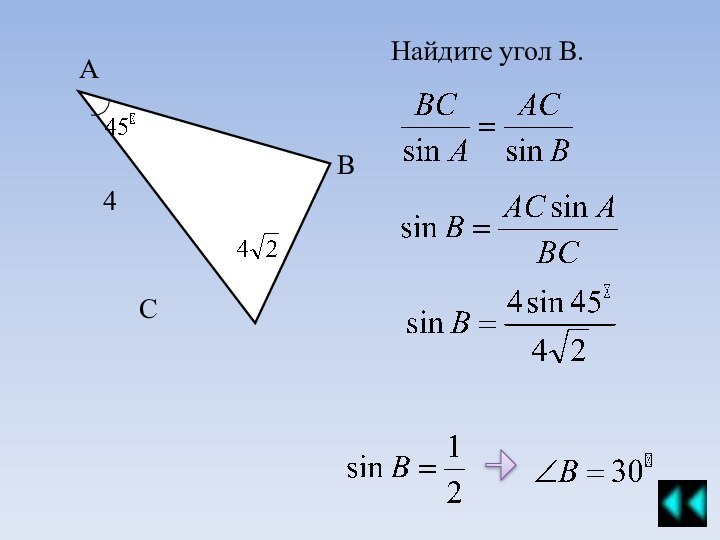
С помощью квеста вы сможете подробно разобрать приведенные примеры и проверить себя с помощью предложенной схемы решения.
Подробно изучив предложенный материал, вам предстоит самостоятельно решить предложенные задачи.
Объединитесь в группы и начните изучение предложенной темы с помощью карты квеста.

такое?

Треугольник – это фигура, состоящая из трёх точек, не

лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки – это вершины, а отрезки – стороны.

Треугольники бывают
остроугольные, прямоугольные, тупоугольные
равнобедренные, равносторонние

Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая

соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору, строгое аксиоматическое доказательство утверждения принадлежит Евклиду.

Также может быть выражена как геометрический факт равенства площади треугольника, отложенного гипотенузы с суммой площадей треугольников, отложенных от катетов. Верно и обратное утверждение: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третей стороны, является прямоугольным.
По мнению историка математики Морица Кантора в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок». В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.
Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (485—410 до н. э),
что Пифагор использовал алгебраические методы,
чтобы находить пифагоровы тройки.

периметр треугольника
Сумма углов в треугольнике равна 180 градусов!
c ^2

=a^2 +b^2 Теорема Пифагора

оценок
Теорема синусов




Теорема косинусов

материалы
Итоги


Справочные
материалы

Гипотенуза прямоугольного
треугольника — это сторона,
Лежащая напротив прямого

угла.
Катеты — стороны, лежащие
напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе.
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе.
Тангенс острого угла в прямоугольном треугольнике —
отношение противолежащего катета к прилежащему.

Критерии оценок

материалы
Итоги


Критерии оценок


Критерии оценок

свою работу, проверив решение задач самостоятельной работы .
Проведите

рефлексию, используя раздел «Критерии оценок».

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

выбери верные/ не верные.
В любой прямоугольный треугольник можно

вписать окружность.
Каждая сторона треугольника больше суммы двух других сторон.
Существует треугольник ABC с меньшей стороной AC и углами ∠A=43 ∘ , ∠C=72 ∘ .
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Любые два равнобедренных треугольника подобны.
Центр окружности, описанной около прямоугольного треугольника, находится на катете этого треугольника.
Если стороны одного треугольника соответственно в 3 раза больше сторон другого, то треугольники подобны.
8. Треугольник, стороны которого равны 7, 12, 13 является прямоугольным.

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

занеси в таблицу:
Критерии оценок
Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

занеси в таблицу:
Критерии оценок
Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

треугольника, является точка пересечения его высот.
Треугольник, стороны которого равны

7, 12, 13 является прямоугольным.
Любые два прямоугольных треугольника подобны.
Центром окружности, вписанной в правильный треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
В треугольнике против меньшего угла лежит меньшая сторона.
Внешний угол треугольника равен сумме внутренних, не смежных с ним.
Существует треугольник с двумя равными тупыми углами. Медиана треугольника делит треугольник на два равных.

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

треугольника, можно найти его площадь.
Если в треугольнике равны два

угла, то он равнобедренный.
Биссектриса угла треугольника делит сторону треугольника пополам.
В равностороннем треугольнике все углы равны.
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.
Центр окружности, вписанной в равнобедренный треугольник, находится в точке пересечения его высот.
Все треугольники со сторонами 3, 4, 5 равны между собой.
Если в треугольнике два угла равны, то треугольник равнобедренный.
Ни в каком треугольнике не может быть два тупых угла.

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

синусов, косинусов:

Критерии оценок
Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

теорему косинусов для вычисления стороны МК:

оценок
Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

= ?
a

боковых сторон равна , а

угол
между ней и одним из оснований равен 1350.
Найдите площадь трапеции.

Задача №2
из ГИА

С

D

А

В

Подсказка (3):

60

S-?

12

18

1350

Н

ВН

север, другой на запад. Скорости их равны
соответственно 12

км/ч и 16 км/ч. Какое
расстояние (в километрах)
будет между ними через 1 час?

Задача №3
из ГИА

С

В

З

Ю

?

12 км/ч

16 км/ч

1 ч

20

F

D

M

12 км

16 км

север, другой на запад. Скорости их равны
соответственно 15

км/ч и 20 км/ч. Какое
расстояние (в километрах)
будет между ними через 2 часа?

Задача №4
из ГИА

С

В

З

Ю

?

15 км/ч

20 км/ч

2 ч

50

F

D

M

30 км

40 км

треугольников:
Критерии оценок
Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

площадь треугольника.

ВН - аsinα
SABC=½АО∙ВН=
½ а ∙b ∙ sinα

такое?
История
Справочные материалы
Итоги


Реши задачи самостоятельно, используя чертежи и определение тангенса

угла.

Критерии оценок

такое?
История
Справочные материалы
Итоги


Критерии оценок



Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го

на ри­сун­ке.

Най­ди­те тан­генс угла, изоб­ра­жен­но­го на ри­сун­ке.