Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему ДВИЖЕНИЯ

Содержание

1. Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.Говорят, что дано отображение плоскости на себя.
Геометрия 9 класс.Тема урока:Движения. 1. Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.Говорят, Рассмотрим примеры отображения плоскости на себя, которые сохраняют расстояние между точками.Любое отображение, Понятие движения в геометрии связано с обычным представлением о перемещении. Но, если Два движения, выполненные последовательно, снова дают движение. Симметрия относительно прямой.Две точки А и А1 называются симметричными относительно прямой аа - ось симметрииАВА1В1Отрезок АВ симметричен отрезку А1В1 относительно прямой аАВ=А1В1?Как можно ММ1аNN1Отрезок МN симметричен отрезку М1N1 относительно прямой аДоказать: MN=M1N1Доказательство:РР1Рассмотрим треугольники NМР и N1М1Р1NP=N1P1MP=M1P1∆NMP=∆N1M1P1MN=M1N1 аАВСПостроить ∆А1В1С1, симметричный ∆АВС относительно прямой а.А1В1С1Как можно проверить 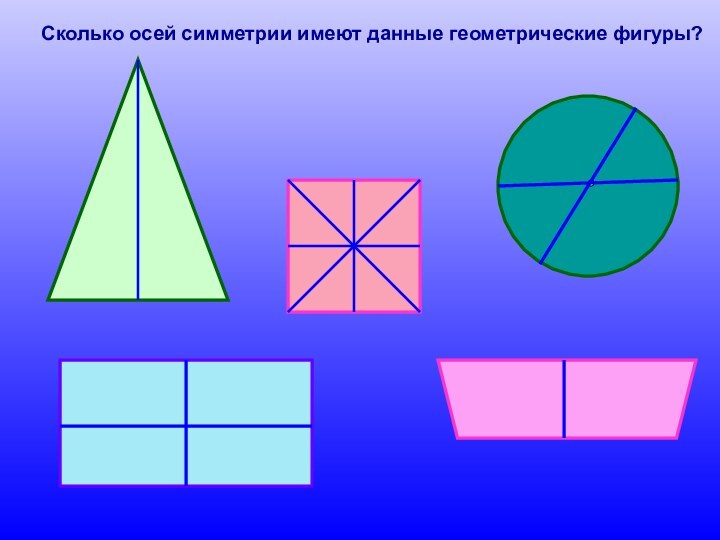Сколько осей симметрии имеют данные геометрические фигуры? С симметрией мы часто встречаемся в быту,архитектуре,технике,природе. Симметрия относительно точки.Две точки А и А1 называются симметричными относительно Построим отрезок А1В1, симметричный отрезку АВ относительно точки О.АВ12А1В1АВ=А1В1?Как можно это проверить? Построить четырёхугольник А1В1С1D1, симметричный четырёхугольнику АВСD относительно точки О.АВСDОА1В1С1D1АВCD= А1В1С1D1?Центральная симметрия – движение. 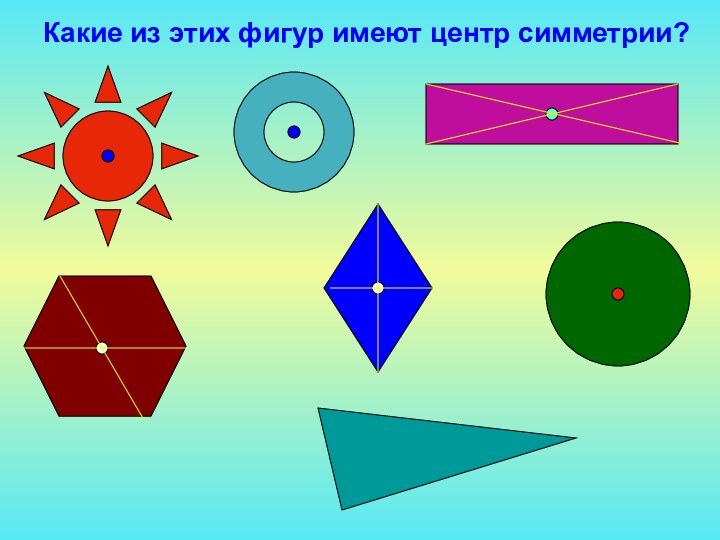Какие из этих фигур имеют центр симметрии? Параллельный перенос.Параллельным переносом на вектор а называется отображение плоскости на себя, Построить отрезок А1В1, который получается из отрезка АВ параллельным переносом на Построить четырёхугольник, который получается из данного четырёхугольника АВСD параллельным переносом на Поворот.Поворотом плоскости вокруг точки О на угол а называется отображение плоскости Построить прямоугольник А1В1С1D1, который получается в результате поворота прямоугольника АВСD вокруг Рассмотренные отображения плоскости на себя:симметрия относительно прямойасимметрия относительно точкиОпараллельный перенос на Практическая работа.1. Построить отрезок А1В1, симметричный отрезку АВ относительно прямой а. а2. Практическая работа.1. Построить ∆А1В1С1, симметричный ∆ АВС относительно прямой а. а2. Построить Домашнее задание. П.113 -116. №1159, 1161, 1164. Дополнительное задание: 1170.
Слайды презентации

Слайд 2 1. Отображение плоскости на себя.









Любая точка плоскости оказывается

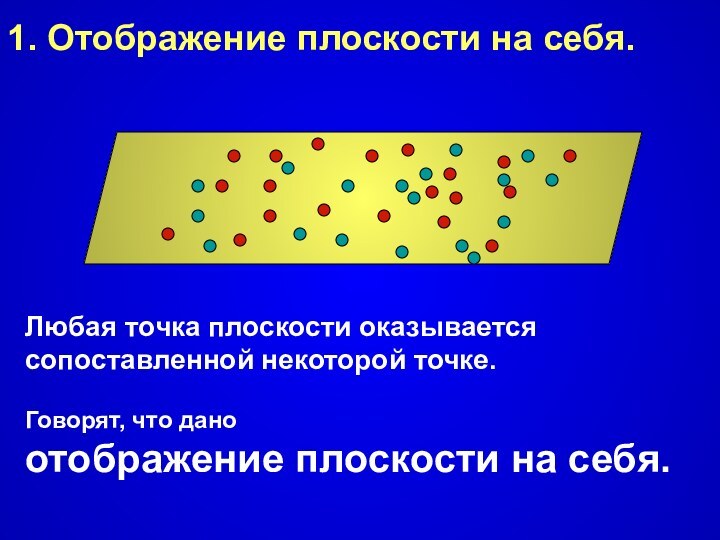
1. Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.Говорят,

сопоставленной некоторой точке.
Говорят, что дано отображение плоскости на себя.






























Слайд 3 Рассмотрим примеры отображения плоскости на себя, которые сохраняют расстояние

Рассмотрим примеры отображения плоскости на себя, которые сохраняют расстояние между точками.Любое

между точками.
Любое отображение, обладающее этим свойством, называется движением.
Движение плоскости –

это отображение плоскости на себя,
сохраняющее расстояния.


Слайд 4

Понятие движения в геометрии связано с обычным представлением о

Понятие движения в геометрии связано с обычным представлением о перемещении. Но,

перемещении. Но, если говоря о перемещении, мы представляем себе непрерывный

процесс, то в геометрии для нас будут иметь значение только начальное и конечное положения фигур.



Слайд 5



Два движения, выполненные последовательно, снова дают движение.

Два движения, выполненные последовательно, снова дают движение.

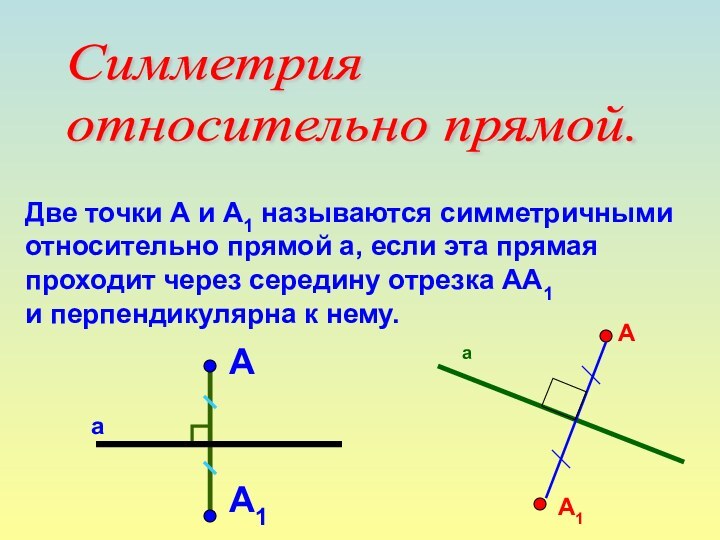
Слайд 6 Симметрия относительно прямой.
Две точки А и А1 называются

Симметрия относительно прямой.Две точки А и А1 называются симметричными относительно прямой

симметричными относительно прямой а, если эта прямая проходит через середину

отрезка АА1 и перпендикулярна к нему.



А

А1

а


а



А

А1


Слайд 7 а
а - ось симметрии
А
В


А1
В1
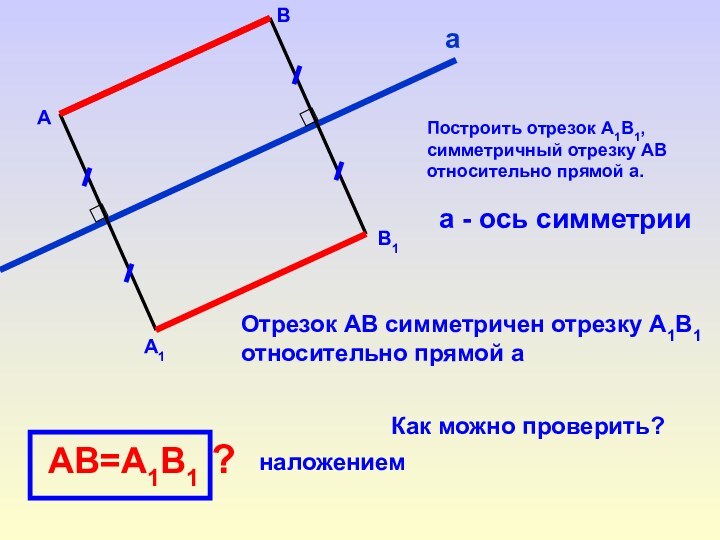
Отрезок АВ симметричен отрезку А1В1 относительно

аа - ось симметрииАВА1В1Отрезок АВ симметричен отрезку А1В1 относительно прямой аАВ=А1В1?Как

прямой а
АВ=А1В1
?
Как можно проверить?

наложением
Построить отрезок А1В1, симметричный отрезку АВ относительно прямой

а.

Слайд 8 М
М1
а
N
N1
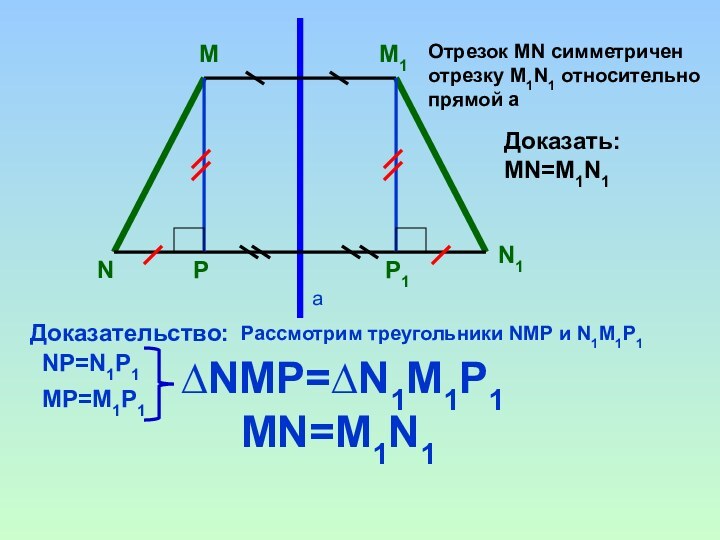
Отрезок МN симметричен отрезку М1N1 относительно прямой а
Доказать: MN=M1N1
Доказательство:
Р
Р1


Рассмотрим треугольники

ММ1аNN1Отрезок МN симметричен отрезку М1N1 относительно прямой аДоказать: MN=M1N1Доказательство:РР1Рассмотрим треугольники NМР и N1М1Р1NP=N1P1MP=M1P1∆NMP=∆N1M1P1MN=M1N1

NМР и N1М1Р1
NP=N1P1
MP=M1P1


∆NMP=∆N1M1P1

MN=M1N1




Слайд 9

а
А
В
С
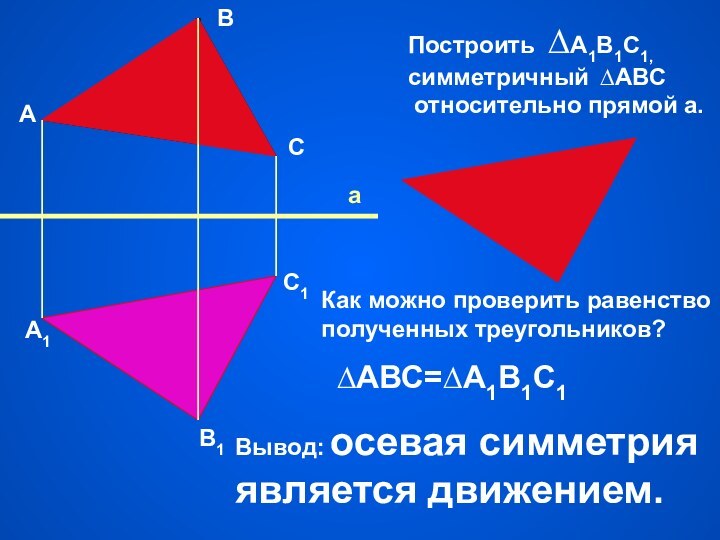
Построить ∆А1В1С1, симметричный ∆АВС относительно прямой а.
А1
В1
С1

Как

аАВСПостроить ∆А1В1С1, симметричный ∆АВС относительно прямой а.А1В1С1Как можно проверить равенство

можно проверить равенство полученных треугольников?
Вывод: осевая симметрия является движением.
∆АВС=∆А1В1С1

Слайд 10 Сколько осей симметрии имеют данные геометрические фигуры?






Сколько осей симметрии имеют данные геометрические фигуры?

Слайд 11 С симметрией мы часто встречаемся
в быту,
архитектуре,
технике,
природе.

С симметрией мы часто встречаемся в быту,архитектуре,технике,природе.

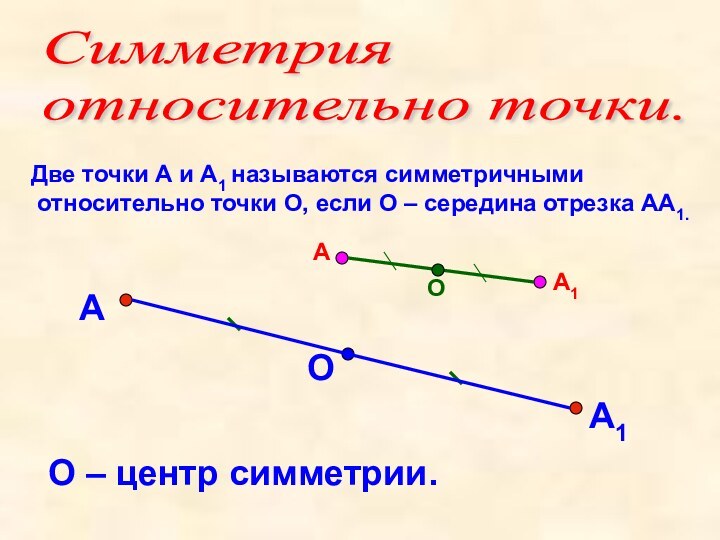
Слайд 12 Симметрия относительно точки.
Две точки А и А1 называются

Симметрия относительно точки.Две точки А и А1 называются симметричными относительно точки

симметричными относительно точки О, если О – середина отрезка

АА1.




О

А

А1

О – центр симметрии.




А

А1

О

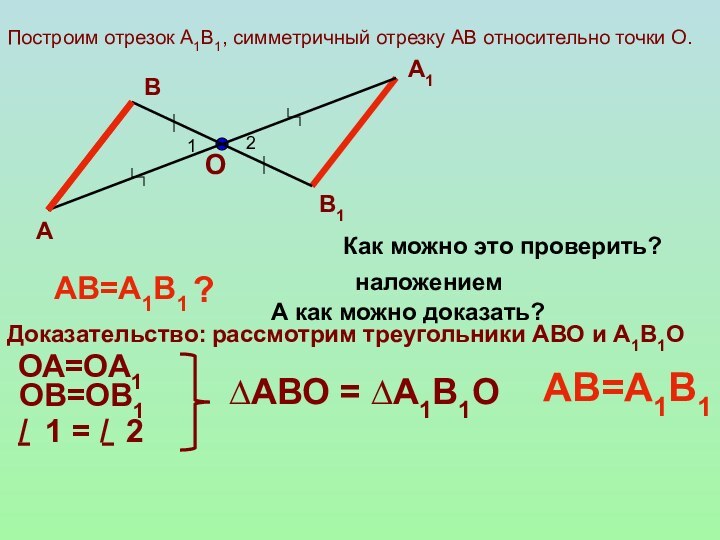
Слайд 13 Построим отрезок А1В1, симметричный отрезку АВ относительно точки

Построим отрезок А1В1, симметричный отрезку АВ относительно точки О.АВ12А1В1АВ=А1В1?Как можно это

О.
А
В

1
2
А1
В1
АВ=А1В1
?
Как можно это проверить?
наложением

Доказательство: рассмотрим треугольники АВО и

А1В1О

ОА=ОА1

ОВ=ОВ1

/ 1 = / 2


∆АВО = ∆А1В1О

АВ=А1В1

О

А как можно доказать?

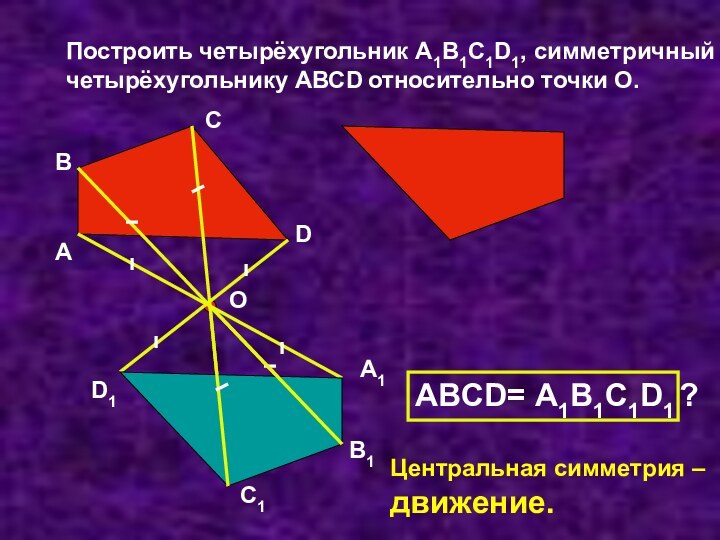
Слайд 14 Построить четырёхугольник А1В1С1D1, симметричный четырёхугольнику АВСD относительно точки

Построить четырёхугольник А1В1С1D1, симметричный четырёхугольнику АВСD относительно точки О.АВСDОА1В1С1D1АВCD= А1В1С1D1?Центральная симметрия – движение.

О.

А
В
С
D

О
А1
В1
С1
D1


АВCD= А1В1С1D1
?

Центральная симметрия – движение.

Слайд 15 Какие из этих фигур имеют центр симметрии?













Какие из этих фигур имеют центр симметрии?

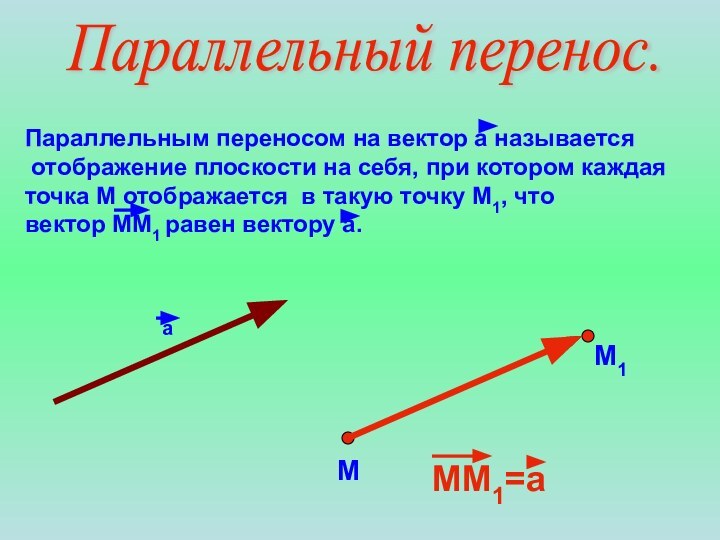
Слайд 16 Параллельный перенос.
Параллельным переносом на вектор а называется отображение

Параллельный перенос.Параллельным переносом на вектор а называется отображение плоскости на себя,

плоскости на себя, при котором каждая точка М отображается

в такую точку М1, что вектор ММ1 равен вектору а.

а


М


М1

ММ1=а

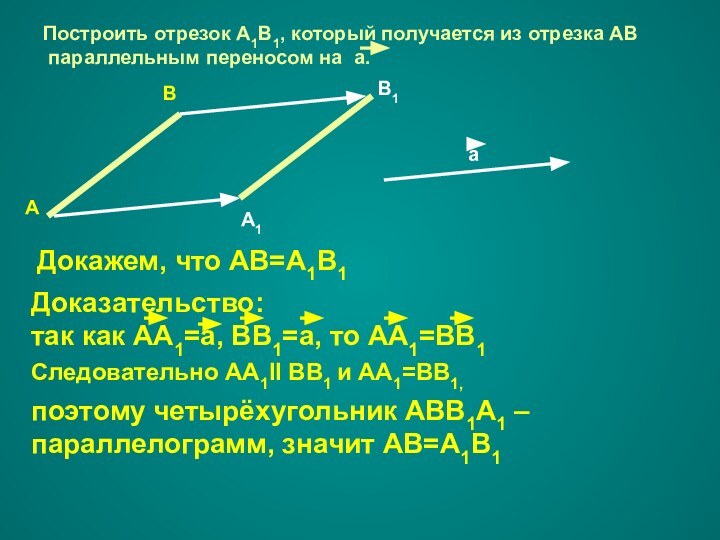
Слайд 17 Построить отрезок А1В1, который получается из отрезка АВ

Построить отрезок А1В1, который получается из отрезка АВ параллельным переносом на

параллельным переносом на а.
А
В
а
А1
В1
Докажем, что АВ=А1В1
Доказательство: так как АА1=а, ВВ1=а,

то АА1=ВВ1

Следовательно АА1II ВВ1 и АА1=ВВ1,

поэтому четырёхугольник АВВ1А1 – параллелограмм, значит АВ=А1В1

Слайд 18
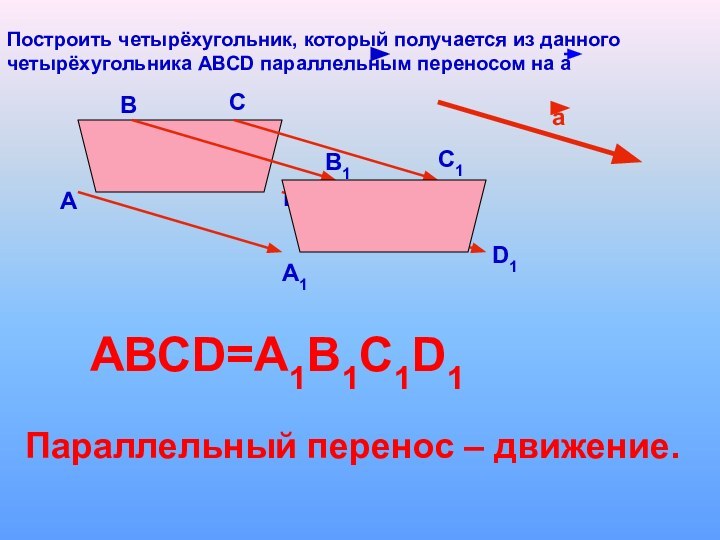
Построить четырёхугольник, который получается из данного четырёхугольника АВСD

Построить четырёхугольник, который получается из данного четырёхугольника АВСD параллельным переносом на а АВСDаА1В1С1D1АВСD=A1B1C1D1Параллельный перенос – движение.

параллельным переносом на а

А
В
С
D
а

А1
В1
С1
D1

АВСD=A1B1C1D1
Параллельный перенос – движение.

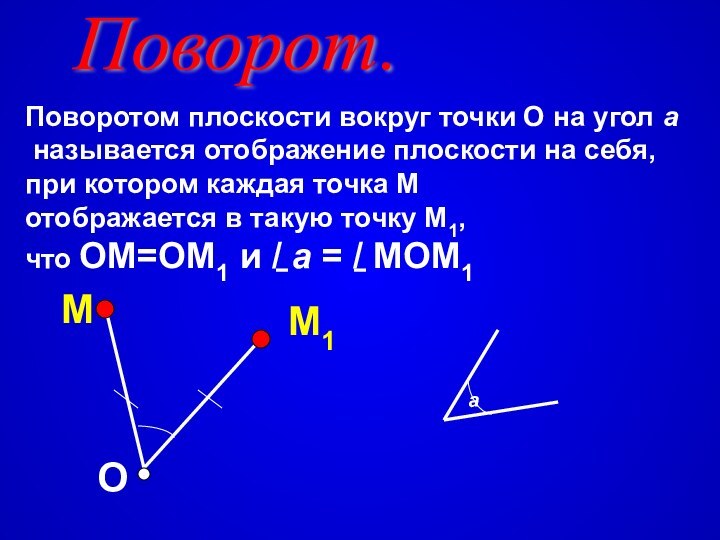
Слайд 19 Поворот.
Поворотом плоскости вокруг точки О на угол а

Поворот.Поворотом плоскости вокруг точки О на угол а называется отображение плоскости

называется отображение плоскости на себя, при котором каждая точка

М отображается в такую точку М1, что ОМ=ОМ1 и / а = / МОМ1


М

О



М1

а

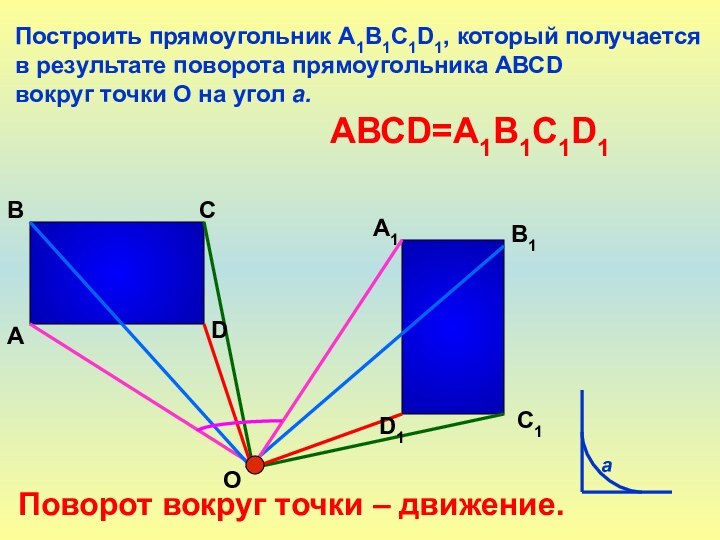
Слайд 20 Построить прямоугольник А1В1С1D1, который получается в результате поворота

Построить прямоугольник А1В1С1D1, который получается в результате поворота прямоугольника АВСD вокруг

прямоугольника АВСD вокруг точки О на угол а.
А
В
С
А1
В1
С1
О


D
D1

а
АВСD=А1В1С1D1
Поворот вокруг точки

– движение.

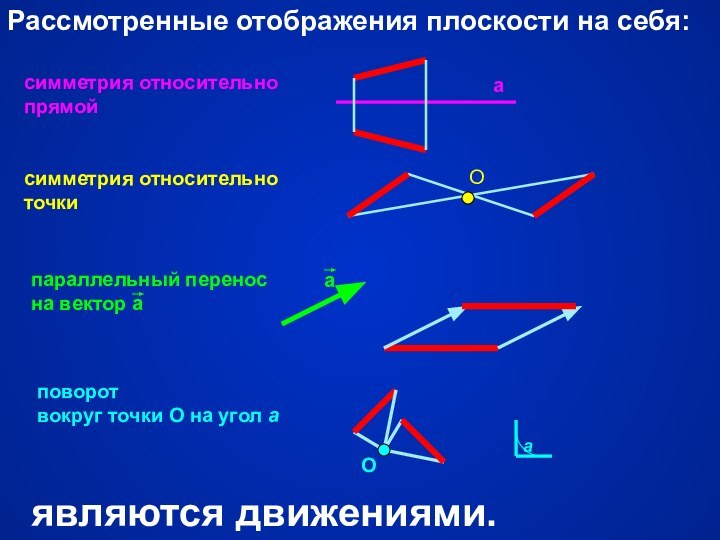
Слайд 21 Рассмотренные отображения плоскости на себя:
симметрия относительно прямой
а
симметрия относительно точки

О
параллельный

Рассмотренные отображения плоскости на себя:симметрия относительно прямойасимметрия относительно точкиОпараллельный перенос на

перенос на вектор а
поворот вокруг точки О на угол а


О

являются движениями.

а


а

Слайд 22 Практическая работа.

1. Построить отрезок А1В1, симметричный отрезку АВ

Практическая работа.1. Построить отрезок А1В1, симметричный отрезку АВ относительно прямой а.

относительно прямой а.
а
2. Построить отрезок А1В1, симметричный отрезку

АВ относительно точки О.

А

В

А

В


О

3.

Построить отрезок А1В1, который получается из отрезка АВ параллельным переносом на а.

а

А

В

«3»

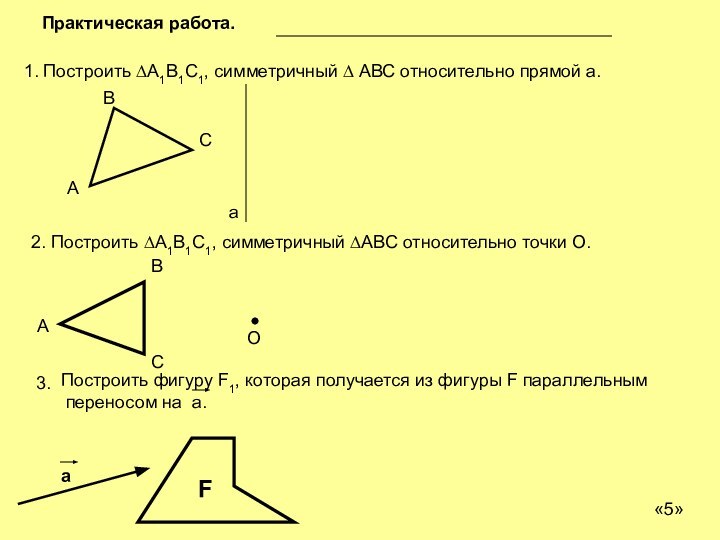
Слайд 23 Практическая работа.

1. Построить ∆А1В1С1, симметричный ∆ АВС относительно

Практическая работа.1. Построить ∆А1В1С1, симметричный ∆ АВС относительно прямой а. а2.

прямой а.
а
2. Построить ∆А1В1С1, симметричный ∆АВС относительно точки

О.

А

В

А

В


О

3.

Построить фигуру F1, которая получается из фигуры F параллельным переносом на а.

а


«5»


С


С


F

  • Имя файла: dvizheniya.pptx
  • Количество просмотров: 178
  • Количество скачиваний: 0
- Предыдущая Значение водорослей
Следующая - Строение живых организмов 6 класс

Похожие презентации

Диктант по геометрии Трапеция Диктант по геометрии Трапеция 189
Окружность круг 5 класс Окружность круг 5 класс 168
Некоторые свойства прямоугольных треугольников Некоторые свойства прямоугольных треугольников 160
Презентация к защите проекта по математике Геометрия и оригами Презентация к защите проекта по математике Геометрия и оригами 177
Презентация по геометрии на тему Подготовка к ОГЭ. Презентация по геометрии на тему Подготовка к ОГЭ. 144
Формула объема многогранника Формула объема многогранника 372
Задачи на построение 7 класс Задачи на построение 7 класс 207
Прямоугольный треугольник Прямоугольный треугольник 160
Жизнь Пифагора Жизнь Пифагора 176
Задачи на нахождение площади Задачи на нахождение площади 184
Луч Луч 150
Второй признак равенства треугольников Второй признак равенства треугольников 144
Прямоугольный параллелепипед геометрия Прямоугольный параллелепипед геометрия 146
В мире треугольников В мире треугольников 192
Презентация по геометрии на тему Аксиома параллельных прямых Презентация по геометрии на тему Аксиома параллельных прямых 134
Равнобедренный треугольник геометрия 7 класс Равнобедренный треугольник геометрия 7 класс 196
Треугольники. Сумма углов треугольника Треугольники. Сумма углов треугольника 170
Геометрические места точек Геометрические места точек 225
Решение задач на тему Прямоугольник. Ромб. Квадрат Решение задач на тему Прямоугольник. Ромб. Квадрат 156
Алгоритм построения точек, симметричных данной относительно прямой Алгоритм построения точек, симметричных данной относительно прямой 162
Площадь квадрата, прямоугольника, параллелограмма Площадь квадрата, прямоугольника, параллелограмма 50
Многоугольники Многоугольники 173
Презентация по теме Аксиомы стереометрии Презентация по теме Аксиомы стереометрии 152
Повторение. Начальные геометрически сведения. Повторение. Начальные геометрически сведения. 172
Тест на знание формул Длина окружности и дуги окружности. Площадь круга и кругового сектора Тест на знание формул Длина окружности и дуги окружности. Площадь круга и кругового сектора 200
Презентация для урока геометрии Площадь ромба Презентация для урока геометрии Площадь ромба 177
Презентация урока Первый признак подобия треугольников 8 класс Презентация урока Первый признак подобия треугольников 8 класс 160
Медиана, биссектриса и высота треугольника Медиана, биссектриса и высота треугольника 165
Цилиндр.Конус.Шар. Цилиндр.Конус.Шар. 205
Задачи на неравенство треугольника Задачи на неравенство треугольника 284