- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электронный образовательный ресурс для дистанционного обучения учащихся 8 класс по теме: Четыре замечательные точки треугольника
Содержание
- 2. ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКАВ четвертой книге
- 3. ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА На вышеназванные четыре
- 4. ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА В двадцатых годах
- 5. В С П О М Н И:Что называется :Медианой треугольника;Биссектрисой треугольника;Высотой треугольника;Серединным перпендикуляром к отрезку
- 6. В С П О М Н ИМедианой
- 7. Четыре замечательные точки треугольникаМЕДИАНЫСЕРЕДИННЫЕ ПЕРПЕНДИКУЛЯРЫВЫСОТЫБИССЕКТРИСЫ
- 8. Первая замечательная точка треугольника- точка пересечения биссектрис
- 9. Реши задачу :Биссектрисы углов А и С
- 10. П Р О В Е Р Ь
- 11. Теорема о серединных перпендикулярах к сторонам треугольникаСерединные
- 12. Третья замечательная точка треугольника –точка пересечения
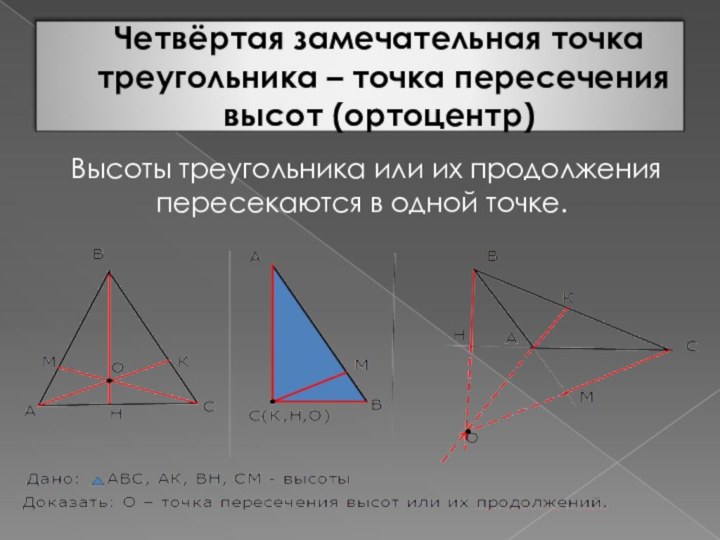
- 13. Четвёртая замечательная точка треугольника – точка
- 14. Теорема о высотах треугольникаПрямые, на которых лежат
- 15. Задача :В остроугольном АВС ,
- 16. Контрольные вопросыДайте определение медиане треугольника.Сформулируйте теорему о
- 17. З А П О М Н И
- 18. Самостоятельная работа 1. В равнобедренном треугольнике АВС с
- 19. Скачать презентацию
- 20. Похожие презентации
ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКАВ четвертой книге "Начал" Евклид решает задачу: "Вписать круг в данный треугольник". Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга. Из решения другой


















Слайд 3
ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА
На вышеназванные четыре точки
было обращено особое внимание, и начиная с XVIII века
они были названы "замечательными" или "особенными" точками треугольника. Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – "геометрии треугольника" или "новой геометрии треугольника", одним из родоначальников которой стал Леонард Эйлер.В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже "прямой Эйлера".
Слайд 4
ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА
В двадцатых годах XIX
века французские математики Ж. Понселе, Ш. Брианшон и другие
установили независимо друг от друга следующую теорему: основания медиан, основания высот и середины отрезков высот, соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же окружности.Эта окружность называется "окружностью девяти точек", или "окружностью Фейербаха", или "окружностью Эйлера". К. Фейербах установил, что центр этой окружности лежит на прямой Эйлера.
Большой вклад в развитие геометрии треугольника внесли математики XIX – XX веков Лемуан, Брокар, Тебо и другие.
Слайд 5
В С П О М Н И:
Что называется
:
Медианой треугольника;
Биссектрисой треугольника;
Высотой треугольника;
Серединным перпендикуляром к отрезку
Слайд 6
В С П О М Н И
Медианой треугольника
называется отрезок, соединяющий любую вершину треугольника с серединой противоположной
стороны.Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороны
Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему.
Слайд 8
Первая замечательная точка треугольника- точка пересечения биссектрис
Дано
:ΔABC, AA₁, BB₁, CC₁ – биссектрисы ΔABC
Доказать :AA₁ ∩
BB₁ ∩ CC₁ = O.Доказательство : Пусть AA₁ ∩ BB₁ = O, тогда если OK, OM, OL – перпендикуляры из O к сторонам ΔABC, то OK=OM, OK=OL – по свойству биссектрисы неразвернутого угла → OL=OM → O лежит на биссектрисе С (на СС₁) → AA1 ∩ BB1 ∩ CC1 = O.
Биссектрисы треугольника пересекаются в одной точке.
Слайд 9
Реши задачу :
Биссектрисы углов А и С треугольника
АВС пересекаются в точке М. Найдите угол АВМ, если
∠???=30°, ∠???=20°А
В
С
М
Слайд 11
Теорема о серединных перпендикулярах к сторонам треугольника
Серединные перпендикуляры
к сторонам треугольника пересекаются в одной точке.
Дано: ΔABC, m-серединный
перпендикуляр к AB, n-серединный перпендикуляр к BC,
p-серединный перпендикуляр к AC.
Доказать: m ∩ n ∩ p = O.
Доказательство: m ∩ n =O, т.к.
если m параллельна n,
то m перпендикулярна BC, и через B
проходят 2 прямые AB, BC,
перпендикулярные к m, чего не может
быть.
По свойству серединного перпендикуляра
к отрезку, OA=OB, OB=OC → OA=OC → O
лежит на серединном перпендикуляре
к AC, т.е. на p → m ∩ n ∩ p=O.
Слайд 12 Третья замечательная точка треугольника –точка пересечения медиан (центроид
- цент тяжести треугольника)
Медианы треугольника пересекаются в одной точке,
которая делит каждую в отношении 2: 1, считая от вершины.Слайд 13 Четвёртая замечательная точка треугольника – точка пересечения высот
(ортоцентр)
Высоты треугольника или их продолжения пересекаются в одной
точке.
Слайд 14
Теорема о высотах треугольника
Прямые, на которых лежат
высоты
треугольника,
пересекаются в одной точке.
Дано: ΔABC, AA₁, BB₁, CC₁
– высоты ΔABC.
Доказать: AA₁ ∩ BB₁ ∩ CC₁ = O.
Доказательство:
Проведем через каждую вершину
ΔABC прямую, параллельную
противоположной стороне. Получим ΔA₂B₂C₂.
A₂C=B₂C, B₂A=C₂A, A₂B=C₂B (объясните почему)
и по построению AA₁, BB₁, CC₁- перпендикуляры к сторонам ΔA₂B₂C₂ → AA₁ , BB₁, CC₁- серединные перпендикуляры к сторонам ΔA₂B₂C₂ → AA₁ ∩ BB₁ ∩ CC₁ = O.
Слайд 15
Задача :
В остроугольном АВС , АD
перпендикулярна ВС, СF перпендикулярна АВ, АD пересекает CF в
точке М.Докажите, что угол АВМ равен углу МСА.
Слайд 16
Контрольные вопросы
Дайте определение медиане треугольника.
Сформулируйте теорему о медианах
треугольника.
Дайте определение биссектрисе треугольника.
Сформулируйте свойство биссектрисы неразвернутого угла и
обратное утверждение.Сформулируйте теорему о биссектрисах треугольника.
Дайте определение серединному перпендикуляру к отрезку.
Сформулируйте свойство серединного перпендикуляра к отрезку и обратное утверждение.
Сформулируйте теорему о серединных перпендикулярах к сторонам треугольника.
Дайте определение высоте треугольника.
Сформулируйте теорему о высотах треугольника.
Слайд 17
З А П О М Н И !
1.
Точка пересечения биссектрис является центром вписанной окружности.
2. Точка пересечения
серединных перпендикуляров к сторонам треугольника является центром описанной окружности.3.Точка пересечения медиан, называется центром тяжести треугольника. (Центроид). .
4. Точка пересечения высот называется ортоцентр.
Слайд 18
Самостоятельная работа
1. В равнобедренном треугольнике АВС с основанием
АС (ВС) (серединный перпендикуляр стороны АВ (АС)пересекает основание АС
(ВС) в точке Р (М). Найдите угол С (угол САМ), если АВР = 52˚(АВС = 43˚)2. Постройте точку на катете прямоугольного треугольника, равноудаленную от гипотенузы и другого катета.
2.Постройте точку на боковой стороне равнобедренного треугольника, равноудаленную от основания и другой боковой стороны.
1 вариант (2 вариант)