- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Как доказать истину в геометрии?
Содержание
- 2. Как доказать истину в геометрии? Авторы:учащиеся
- 3. Цель исследования: Найти с помощью чего и
- 4. Вопросы исследования:Что такое геометрия? Строим дом под названием «Геометрия».Для чего нужна геометрия? Примеры доказательств.
- 5. Возникновение геометрии.Слово «ГЕОМЕТРИЯ» древнегреческого происхождения.ГЕОМЕТРИЯ – гео-
- 6. Стереометрия (stereo-пространство)Планиметрия(planum-равнинаплоскость)Школьный курс геометрии делится на два
- 7. Дом «ГЕОМЕТРИЯ»АКСИОМЫ и ПОСТУЛАТЫПостроим домТЕОРЕМЫТЕОРЕМЫЗАДАЧИДругие разделы математики
- 8. Аксиомы и постулаты.Существует набор исходных посылок, называемых
- 9. Легенда “О происхождении аксиом.” Было это в
- 10. К числу геометрических аксиом относятся, например, следующие:
- 11. Задание 1. У Вас в наличии малярная
- 12. Аксиомы и постулаты.Следующий ПОСТУЛАТ касается построений и
- 13. Теоремы.На основе аксиом и определений чисто логическим
- 14. Теоремы.Так что же это такое - теорема?Под
- 15. Доказательство.Когда же появились первые доказательства? И тут
- 16. Теоремы.Теорема. Вертикальные углы равны.
- 17. 3). Можно ли при доказательстве утверждений
- 18. Вывод Математическое доказательство истины в геометрии проводится
- 19. Скачать презентацию
- 20. Похожие презентации


















Слайд 3
Цель исследования:
Найти с помощью чего и как
в геометрии доказывается истинность того или иного математического утверждения?
Слайд 4
Вопросы исследования:
Что такое геометрия?
Строим дом под названием
«Геометрия».
Для чего нужна геометрия? Примеры доказательств.
Слайд 5
Возникновение геометрии.
Слово «ГЕОМЕТРИЯ» древнегреческого происхождения.
ГЕОМЕТРИЯ – гео- «земля»,
метрио- «измеряю».
Причина возникновения: практическая деятельность людей (различные измерительные работы при: разметке земельных участков,проведении дорог, строительстве зданий,…).
ГЕОМЕТРИЯ, раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения.
дополнительно
ИСТОРИЯ
Слайд 6
Стереометрия
(stereo-пространство)
Планиметрия
(planum-равнина
плоскость)
Школьный курс геометрии делится на два раздела:
Разделы
курса геометрия
ГЕОМЕТРИЯ на плоскости
ГЕОМЕТРИЯ в пространстве
«планиметрия» – наименование смешанного происхождения:
от греч. metreo – измерять
и лат. planum – плоская поверхность (плоскость)«стереометрия» – от греч. stereos – пространственный (stereon – объем).
Слайд 8
Аксиомы и постулаты.
Существует набор исходных посылок, называемых аксиомами
и постулатами, на которых базируется вся структура геометрии.
АКСИОМЫ
– это утверждения, принимаемые за истинные без доказательств. Аксиомы обычно подразделяются на две группы: общие, относящиеся ко всей математике, и геометрические. На уроке геометрии.
Учитель: "Для чего мы изучаем аксиомы?"
Ученик: "Чтобы их не доказывать".
Слово "постулат" происходит от латинского слова "postulatum", обозначающего требование.
Аксиома - греч. "axioma" - авторитетное предложение "то, что приемлемо"
Слайд 9
Легенда “О происхождении аксиом.”
Было это в Древнем Египте.
Огромная река течет через всю эту местность — Нил.
Разливаясь с каждой весной, Нил затоплял поля и уничтожал межи, разделявшие земельные участки. Межи приходилось восстанавливать каждый раз заново. Из года в го, из века в век совершенствовались приемы землемерия. Если произнести это слово на древнегреческом языке, мы узнаем в нем название науки, о которой рассуждаем: геометрия.Натягивая межевую веревку между двумя колышками, древние землемеры не раз имели возможность убедиться, что это несложная операция всегда приводит к одному и тому же результату.
Многократно повторенный опыт внушал вывод:
Через две точки можно провести прямую, и притом только одну.
Так рождались аксиомы, общие для всех, к то трудиться на земле.
Слайд 10
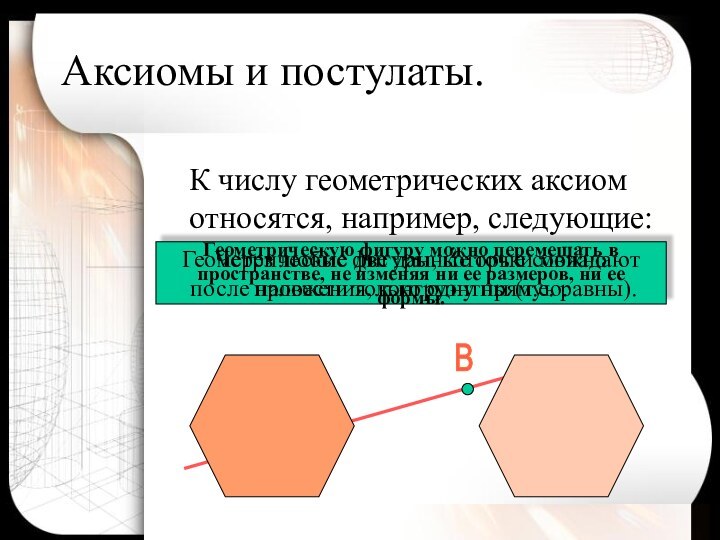
К числу геометрических аксиом относятся, например, следующие:
Аксиомы
и постулаты.
Через любые две данные точки можно
провести только
одну прямую. А
В
Геометрическую фигуру можно перемещать в
пространстве, не изменяя ни ее размеров, ни ее формы.
Геометрические фигуры, которые совпадают
после наложения, конгруэнтны (т.е. равны).
Слайд 11 Задание 1. У Вас в наличии малярная кисть,
плакатное перо и тонко очиненный карандаш.
Каким из этих
инструментов вы бы воспользовались, чтобы нарисовать прямую линию на бумаге? (Посмотрите на след через лупу, анализируйте ответ и сделайте вывод).Подумай…
Слайд 12
Аксиомы и постулаты.
Следующий ПОСТУЛАТ касается построений и принимается
за истину без доказательств:
Окружность может быть описана вокруг
любойданной точки как центра и с любым радиусом.
Слайд 13
Теоремы.
На основе аксиом и определений чисто логическим путем
выводятся новые утверждения о первичных и определяемых понятиях. Получаемые
новые утверждения называются ТЕОРЕМАМИ
Слайд 14
Теоремы.
Так что же это такое - теорема?
Под ТЕОРЕМОЙ
в математике понимают любое математическое утверждение, справедливость которого устанавливается
с помощь доказательства.ЗАКЛЮЧЕНИЕ
(то, что требуется
доказать)
УСЛОВИЕ
(то, что дано)
ТЕОРЕМА
Слайд 15
Доказательство.
Когда же появились
первые доказательства?
И тут сквозь
дым времен перед
нами предстает удивительный
человек, знаменитый мудрец из
древнегреческого города Милет. С поразительным единодушием историки науки присваивают звание первоматематика Фалесу Милетскому (625-527 гг. до н.э.).
ФАЛЕС
(625-527 г.г. до н.э)
Слайд 16
Теоремы.
Теорема. Вертикальные углы равны.
Дано: ∠AOB и ∠COD –
вертикальные.
Доказать: ∠AOB = ∠COD.
Доказательство. Так как ∠AOB и ∠COD – вертикальные, то лучи OB и OD – дополнительные, следовательно, ∠AOB и ∠AOD – смежные. Аналогично, ∠COD и ∠AOD – смежные. По свойству смежных углов: ∠AOB + ∠AOD = 180° и ∠COD + ∠AOD = 180°. Имеем: ∠AOB = 180° – ∠AOD и ∠COD = 180° – ∠AOD, значит, ∠AOB = ∠COD, ч. т. д.
В
А
С
О
D
Слайд 17 3). Можно ли при доказательстве утверждений опираться
на
ранее доказанные теоремы или только на аксиомы?
ТЕСТ.
Проверь себя
1). Что является основой геометрии, аксиомы или теоремы?
теоремы
аксиомы и теоремы
нет ответа
аксиомы
2). Возможно ли произвести доказательство аксиом?
нет
незнаю
лишь некоторых
да
4). Всегда ли необходимо производить доказательство теорем?
нет, очевидные доказательства можно опустить
а)
б)
да
в)
да, кроме прямых следствий из аксиом
г)
нет правильного ответа.
только на
теоремы
лишь на
аксиомы
нет ответа
можно и на
теоремы