- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Теорема о пересечении высот треугольника (8класс)
Содержание
- 2. Этапы урока: организационный;этап проверки домашнего задания;актуализация знаний учащихся;объяснение нового материала;закрепление;проверка усвоения.Тип урока: усвоение новых знаний
- 3. Рассмотреть теорему о пересечении высот треугольника.
- 4. Сформулируйте определение серединного перпендикуляра Сформулируйте свойство
- 5. • точка пересечения медиан; • точка пересечения
- 6. Высоты треугольника (или их продолжения) пересекаются в одной точке.Теорема
- 7. 1. В ∆АBC опущены перпендикуляры: AA1
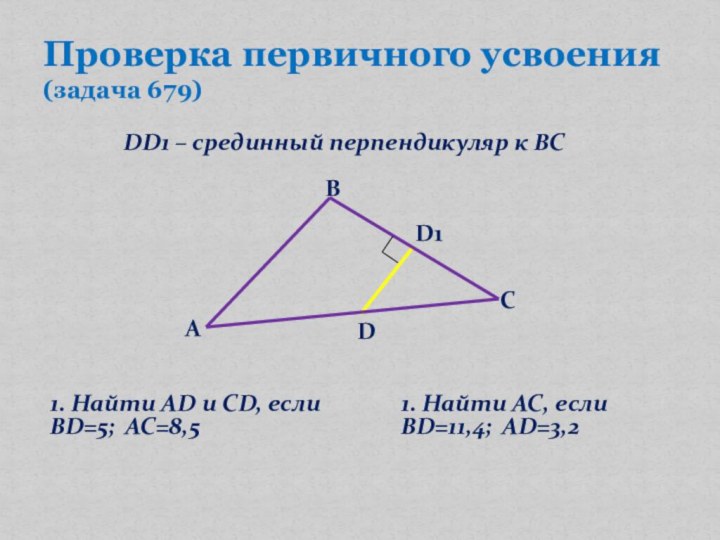
- 8. Проверка первичного усвоения (задача 679)ABCD1. Найти AD
- 9. биссектрисы медианы серединные перпендикулярывысотыКакие элементы треугольника пересекаются в одной точке?
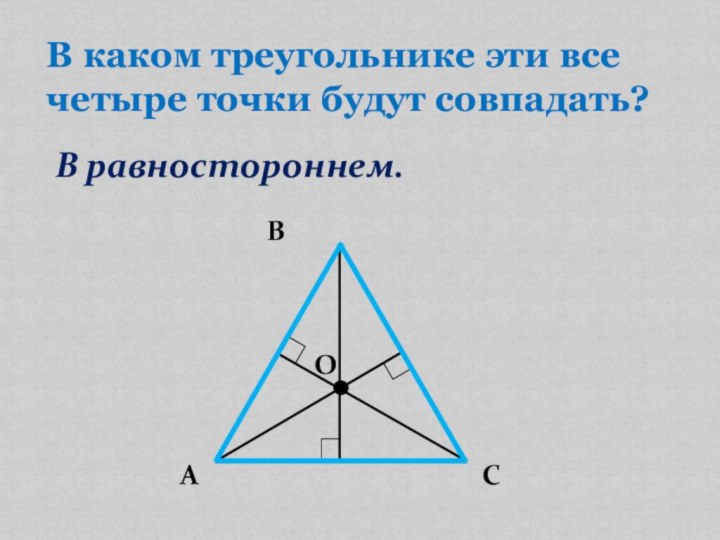
- 10. В каком треугольнике эти все четыре точки будут совпадать?В равностороннем.AВСО
- 11. Домашнее задание П. 76, вопрос 20 (стр. 185)Задача 685
- 12. Скачать презентацию
- 13. Похожие презентации
Этапы урока: организационный;этап проверки домашнего задания;актуализация знаний учащихся;объяснение нового материала;закрепление;проверка усвоения.Тип урока: усвоение новых знаний








Слайд 2
Этапы урока:
организационный;
этап проверки домашнего задания;
актуализация знаний учащихся;
объяснение
нового материала;
Слайд 3
Рассмотреть теорему о пересечении высот треугольника.
Учить
применять данную теорему при решении задач.
Формировать умения применять известные
знания в незнакомой ситуации, сравнивать, анализировать, обобщать.Цели урока:
Слайд 4
Сформулируйте определение серединного перпендикуляра
Сформулируйте свойство точки,
лежащей на серединном перпендикуляре
Сформулируйте обратное утверждение
Каким свойством обладают серединные
перпендикуляры в треугольнике?Повторение (устный опрос ):
Слайд 5
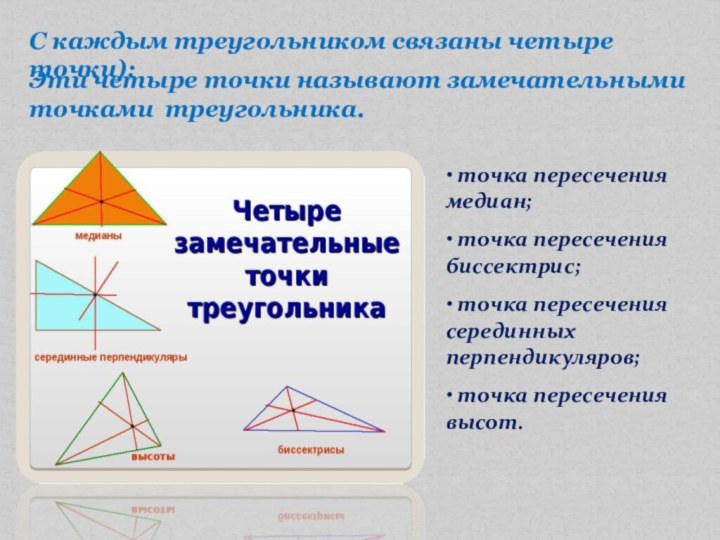
• точка пересечения медиан;
• точка пересечения биссектрис;
• точка пересечения серединных перпендикуляров;
• точка пересечения высот.
C каждым треугольником связаны четыре точки):
Эти четыре точки называют замечательными точками треугольника.
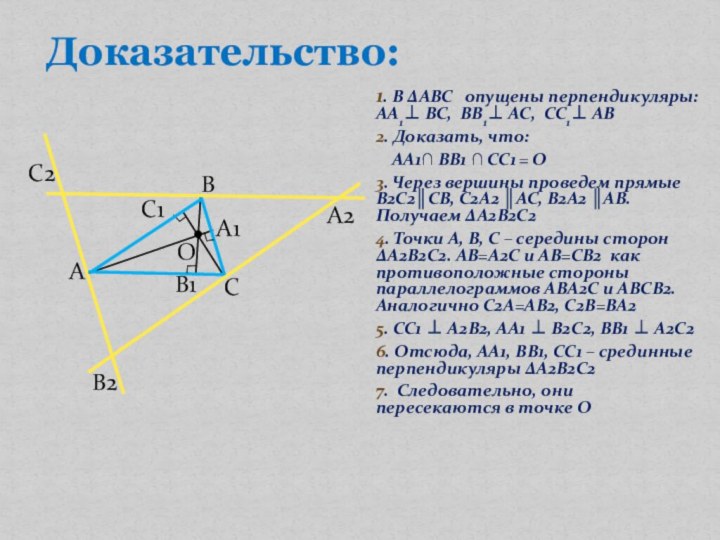
Слайд 7 1. В ∆АBC опущены перпендикуляры: AA1 BC,
BB1 AC, CC1 AB
2. Доказать, что:
AA1 BB1
CC1 = O 3. Через вершины проведем прямые В2С2║СВ, С2А2 ║АС, В2А2 ║АВ. Получаем ∆А2B2C2
4. Точки А, B, С – середины сторон ∆А2B2C2. АВ=А2С и АВ=СВ2 как противоположные стороны параллелограммов АВА2С и АВСВ2. Аналогично С2А=АВ2, С2В=ВА2
5. СС1 А2В2, АА1 В2С2, ВВ1 А2С2
6. Отсюда, АА1, ВВ1, СС1 – срединные перпендикуляры ∆А2B2C2
7. Следовательно, они пересекаются в точке О
Доказательство:
C2
B2
А2
О