- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)
Содержание
- 2. Расстояние от точки до плоскостиМетодыПоэтапно-вычислительный методМетод параллельных прямых и плоскостейВекторный методКоординатный методМетод объемов
- 3. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра
- 4. В единичном кубе ABCDA1B1C1D1 найти расстояние
- 5. В единичном кубе ABCDA1B1C1D1 найти расстояние
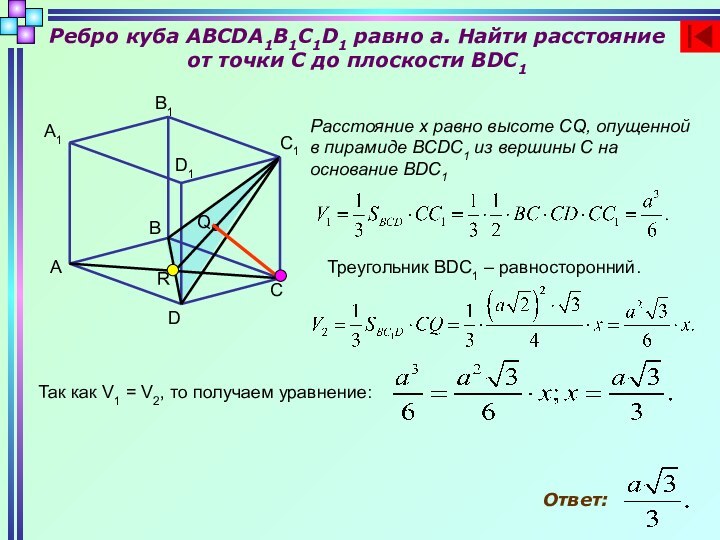
- 6. DCBAA1B1D1MC1Имеем:Отсюда получаем:Таким образомОтвет:
- 7. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра
- 8. Скачать презентацию
- 9. Похожие презентации





Слайд 2
Расстояние от точки до плоскости
Методы
Поэтапно-вычислительный
метод
Метод параллельных
прямых
и плоскостей
Слайд 3
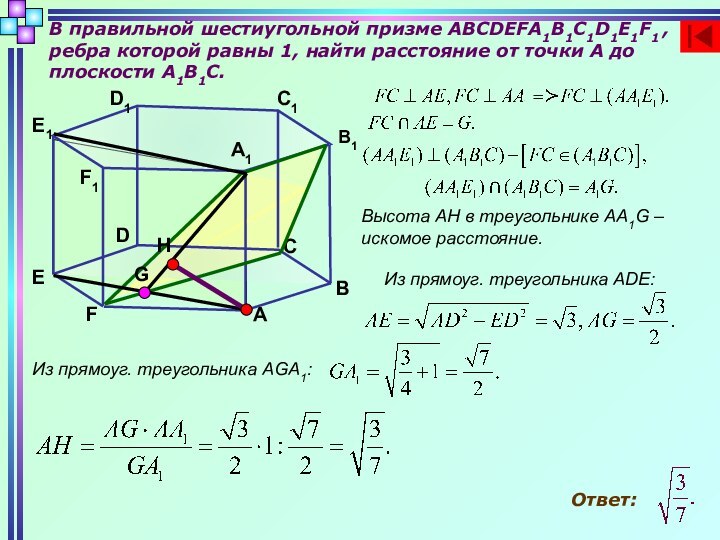
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой
равны 1, найти расстояние от точки А до плоскости
А1В1С.B
C
D
A
C1
D1
E1
F1
A1
B1
E
F
G
H
Высота АН в треугольнике АА1G – искомое расстояние.
Из прямоуг. треугольника ADE:
Из прямоуг. треугольника AGA1:
Ответ:
Слайд 4 В единичном кубе ABCDA1B1C1D1 найти расстояние
от точки C1 до плоскости AB1C
B
D
C
A
A1
B1
C1
D1
то
Поэтому искомое расстояние h равно расстоянию от произвольной точки А1С1 до плоскости АВ1С.
Е
О
О1
h
Обозначим расстояние от О1 до (АВ1С) через h.
Покажем, что О1Е ┴ АВ1С.
О1Е – перпендикуляр к (АВ1С), а О1Е = h
Так как
то из прямоугольного треугольника ОВ1О1:
Искомое расстояние:
Ответ:
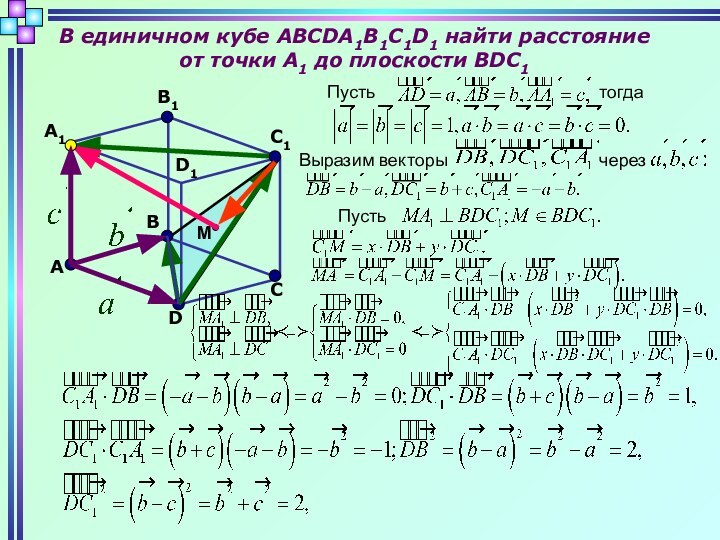
Слайд 5 В единичном кубе ABCDA1B1C1D1 найти расстояние
от точки А1 до плоскости BDC1
D
C
B
A
A1
B1
D1
M
C1
Пусть
тогда
Выразим векторы
через
Пусть
Слайд 7 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой
равны 1, найти расстояние от точки А до плоскости
DEF1B
C
D
A
C1
D1
E1
F1
A1
B1
E
F
O
z
y
x
Введем систему координат и найдем координаты точек:
уравнение (DEF1).
Подставим координаты точек D, E, F1 в уравнение:
уравнение (DEF1):
Ответ: