Презентация на тему Многогранник 1

основе определения многогранников).

Доказать почему существует только 5 типов правильных

многогранников.

Рассмотреть свойства правильных многогранников.

Познакомить с историческими фактами, связанными с теорией правильных многогранников.

Показать, как можно с помощью куба построить другие виды правильных многогранников.

совокупностью конечного числа плоских многоугольников, соединённых таким образом, что

каждая сторона любого многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами.

правильными многоугольниками, и все многогранные углы при вершинах равны.

Приведён пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.

правильных n – угольников, чтобы сумма их углов была

меньше 3600. Т.е должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)

и в каждой вершине сходится по три ребра и

по три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.

назад

ТЕТРАЭДР

и в каждой вершине сходится по четыре ребра и

по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер

назад

и в вершине сходится по пять рёбер и граней.

У икосаэдра:20 граней, 12 вершин и 30 ребер

назад

и в каждой вершине сходится по три ребра и

три грани. У него: 6 граней, 8 вершин и 12 ребер.

назад

в каждой вершине сходится по три ребра и три

грани. У додекаэдра:12 граней, 20 вершин и 30 ребер.

назад

Древней Греции – именно им посвящена завершающая, XIII книга

«Начал» Евклида.

занимали видное место в идеалистической картине мира древнегреческого философа

Платона.

Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.

правильные многоугольники;
В каждой вершине сходится одно число граней;
Все его

двугранные углы равны.

первых дошедших до нас теоретических трактатов по математике. Годы

жизни - около 365 - 300 до н.э.
О жизни Евклида почти ничего не известно. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: "Евклид, сын Наукрата, известный под именем "Геометра", ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира".
Он родился в АфинахОн родился в Афинах, учился в Академии. В начале 3 века до н.э. переехал в Александрию и там основал математическую школу и написал для ее учеников свой фундаментальный труд, объединенный под общим названием "НАЧАЛА". Он был написан около 325 года до нашей эры. 

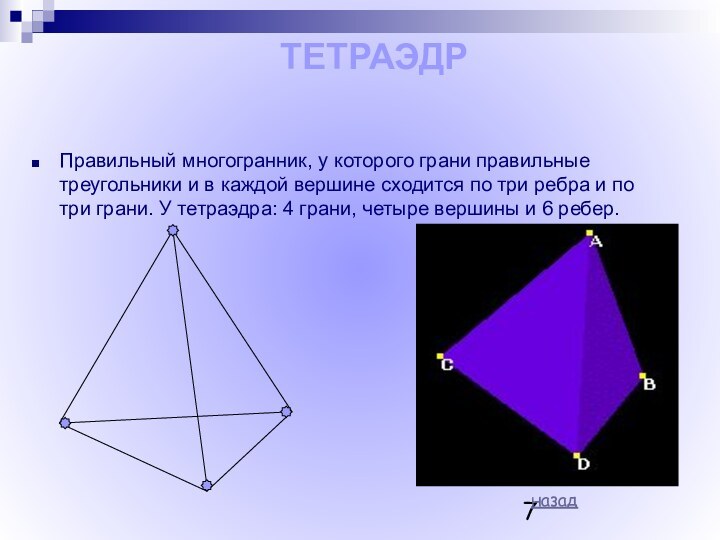
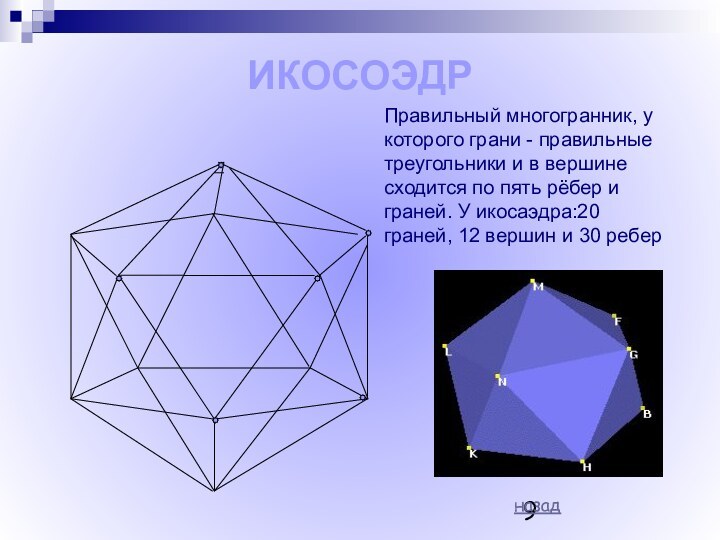
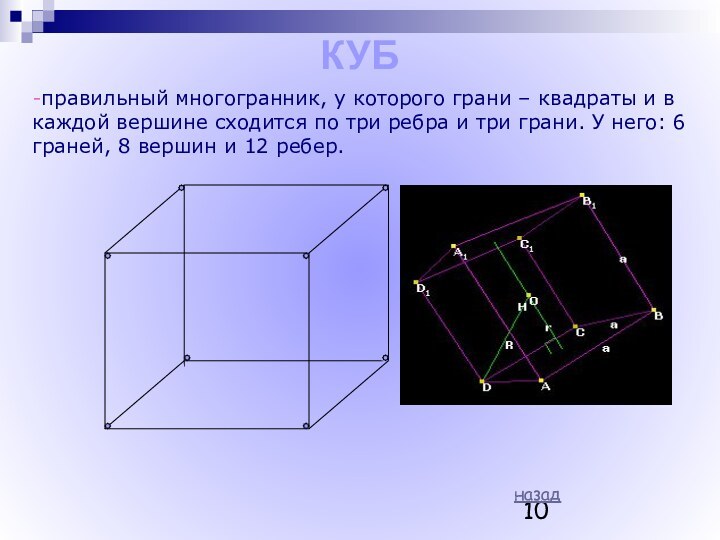
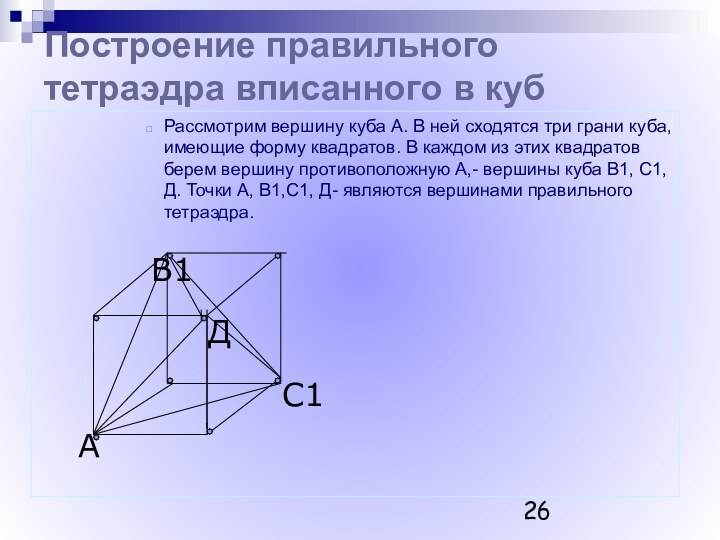
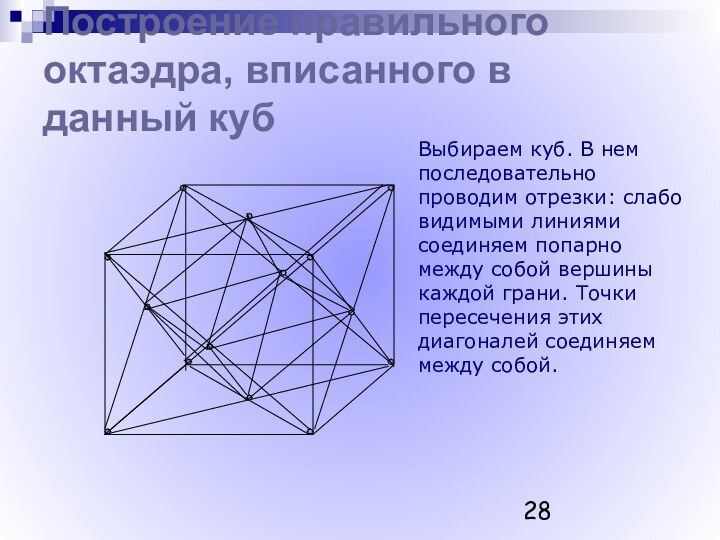
Платон (Platon) (род. 427 - ум. 347 гг.до н.э.)

- греческий философ. Родился в Афинах. Настоящее имя Платона было Аристокл. Прозвище Платон (Широкоплечий) было ему дано в молодости за мощное телосложение. Происходил из знатного рода и получил прекрасное образование. Возможно, слушал лекции гераклитика Кратила, знал популярные в Афинах сочинения Анаксагора, был слушателем Протагора и других софистов. В 407 г. стал учеником Сократа, что определило всю его жизнь и творчество. Согласно легенде, после первого же разговора с ним Платон сжег свою трагическую тетралогию, подготовленную для ближайших Дионисий. Целых восемь лет он не отходил от любимого учителя, образ которого он с таким пиететом рисовал впоследствии в своих диалогах. В 399 г. Сократ, приговоренный к смерти, закончил жизнь в афинском узилище. Платон, присутствовавший на процессе, не был с Сократом в его последние минуты. Возможно, опасаясь за собственную жизнь, он покинул Афины и с несколькими друзьями уехал в Мегару. Оттуда он поехал в Египет и Кирену (где встретился с Аристиппом и математиком Феодором), а затем в Южную Италию — колыбель элеатизма (Парменид, Зенон Элейский) и пифагорейства (Пифагор).

все стороны и все углы равны.

А. В ней сходятся три грани куба, имеющие форму

квадратов. В каждом из этих квадратов берем вершину противоположную А,- вершины куба В1, С1, Д. Точки А, В1,С1, Д- являются вершинами правильного тетраэдра.

Д

В нем последовательно проводим отрезки: слабо видимыми линиями соединяем

попарно между собой вершины каждой грани. Точки пересечения этих диагоналей соединяем между собой.

граней куба проведем прямые,
которые пересекаются в точке О-

центре куба- и являются взаимно перпендикулярными. На каждой из этих прямых по обе стороны от точки О отложим отрезки длиной 1,5 а,
Где а- длина ребра куба. Концы этих отрезков являются вершинами правильного октаэдра. Далее последовательно соединяем эти вершины.

O

граней куба по одному отрезку одинаковой длины с концами

на равных расстояниях от ребер. Расположим отрезки и выберем их длину так, чтобы соединяя концы отрезка одной грани с концом отрезка другой грани получить равносторонний треугольник, причем из каждой вершины должны выходить пять ребер.