Слайд 2
Пифагор Самосский (570 — 490 гг.до н. э.)
—
древнегреческий философ и математик,
создатель религиозно-философской школы пифагорейцев.
Давно решил наш
Пифагор,
Проверить «правило верёвки»,
Но не докажешь ничего
Без логики, ума, сноровки.
Он сам трудился – Пифагор
Над этой трудною задачей,
И в день один пришла пора
Поздравить гения с удачей.
И вот уже и стар и млад,
С серьёзным видом, без улыбки
Ту теорему доказать
Мечтают со своей попытки.
И к настоящему моменту,
За столько долгих-долгих лет
Сто доказательств теоремы
Нам появилися на свет.
Как много лет прошло с тех пор,
И воды с гор крутых сбегало,
Когда Эвклид своим путём
Доказывал её в «Началах».
Слайд 3
Высказывания, цитаты и афоризмы Пифагорa
• Не делай ничего

постыдного ни в присутствии других, ни втайне. Первым твоим
законом должно быть уважение к себе самому.
• Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.
• Неразумные при выпивании вина доходят до опьянения, а при несчастьях — до совершенной потери ума.
• Никто не должен преступать меру ни в пище, ни в питии.
• Будь благословенно божественное число, породившее богов и людей.
• Будь другом истины до мученичества, но не будь ее защитником до нетерпимости.
• Полезнее наобум бросить камень, чем пустое слово.
• Прежде всего не теряй самоуважения!
• Берегите слезы ваших детей, дабы они могли проливать их на вашей могиле.
• Благоразумная супруга! Если желаешь, чтобы муж твой свободное время проводил подле тебя, то постарайся, чтоб он ни в каком ином месте не находил столько приятности, удовольствия, скромности и нежности.
• Все исследуй, давай разуму первое место.
• Две вещи делают человека богоподобным: жизнь для блага общества и правдивость.
• Делай великое, не обещая великого.
• Для познания нравов какого ни есть народа старайся прежде изучить его язык.
• Если можешь быть орлом, не стремись стать первым среди галок.
• В общественных отношениях своих избегай делать врагов из друзей; старайся, наоборот, обращать своих врагов в друзей.
• Во время гнева не должно ни говорить, ни действовать.
• Живи с людьми так, чтобы твои друзья не стали недругами, а недруги стали друзьями.
Слайд 4
Многие при имени Пифагор вспоминают его теорему. Но

неужели мы можем встречать эту теорему только в геометрии?
Нет, конечно, нет! Теорема Пифагора встречается в разных областях наук. Например: в физике, астрономии, архитектуре и в других. Но так же Пифагор и его теорема воспеты в литературе.
Существуют много легенд, мифов, рассказов, песен, притчей, небылиц, анекдотов, частушек об этой теореме. Ниже приводятся примеры каждого вида, перечисленного здесь…
Легенды и мифы
Легенда о смерти Пифагора
Сонную тишину ночного Метапонта прорезал ужасный крик. Послышалось падение на землю тяжелого тела, топот убегающих ног, и все смолкло. Когда ночной караул прибыл на место происшествия, в колеблющемся свете факелов все увидели распростертого на земле старца, и неподалеку от него - мальчик 12 с лицом, перекошенным от ужаса.
- Кто это? - спросил начальник караула у мальчика
- Это Пифагор, - ответил тот.
- Кто такой Пифагор? Среди жителей города нет гражданина с таким именем.
- Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов, и выходил только ночью. Они выследили его и убили.
- Сколько их было?
- Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него. Начальник караула стал на колени и приложил руки к груди старца.
- Конец, - сказал начальник.
Слайд 5
Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии,
устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин
катетов равна квадрату длины гипотенузы.
Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору.
Слайд 6
Из истории
Строго говоря, хоть теорема и называется «теоремой

Пифагора», сам Пифагор ее не открывал. Прямоугольный треугольник и
его особенные свойства изучались задолго до него. Есть две полярных точки зрения на этот вопрос. По одной версии Пифагор первым нашел полноценное доказательство теоремы. По другой доказательство не принадлежит авторству Пифагора.
Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал.
Также сегодня известно, что задачи о прямоугольном треугольнике встречаются в египетских источниках времен фараона Аменемхета I, на вавилонских глиняных табличках периода правления царя Хаммурапи, в древнеиндийском трактате «Сульва сутра» и древнекитайском сочинении «Чжоу-би суань цзинь».
Как видите, теорема Пифагора занимала умы математиков с древнейших времен. Подтверждением служит и около 367 разнообразных доказательств, существующих сегодня. В этом с ней не может тягаться ни одна другая теорема. Среди знаменитых авторов доказательств можно вспомнить Леонардо да Винчи и двадцатого президента США Джеймса Гарфилда. Все это говорит о чрезвычайной важности этой теоремы для математики: из нее выводится или так или иначе с нею связано большинство теорем геометрии.
Слайд 7
Рисунок из книги Чжоу би суань цзин (500—200
лет до нашей эры)
В древнекитайской книге «Чжоу би суань
цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы
Слайд 8
Доказательство теоремы Пифагора
Посмотрите на равнобедренный прямоугольный треугольник ABC:
На гипотенузе АС можно построить квадрат, состоящий из четырех
треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:
Слайд 10
Доказательство 1
Для самого простого доказательства теоремы Пифагора для
прямоугольного треугольника нужно задать идеальные условия: пусть треугольник будет
не только прямоугольным, но и равнобедренным. Есть основания полагать, что именно такой треугольник первоначально рассматривали математики древности.
Утверждение «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» можно проиллюстрировать следующим чертежом:
Доказательство теоремы Пифагора
Посмотрите на равнобедренный прямоугольный треугольник ABC: На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:
Слайд 11
Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]
Слайд 12
Доказательства
В научной литературе зафиксировано
не менее 400 доказательств
теоремы Пифагора
Посмотри ещё одно своеобразное доказательство теоремы Пифагора:
Слайд 15
Примеры Пифагоровых троек:
(3, 4, 5), (6, 8,
10), (5, 12, 13), (9, 12, 15), (8, 15,
17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) и т.д.
Пифагоровы тройки, например, имеются на глиняной табличке Plimpton 322: это древневавилонский клинописный текст (XIX—XVII вв. до н. э.).
Слайд 16
Практическое применение теоремы
Теорема Пифагора находит применение не только
в математике, но и в архитектуре и строительстве, астрономии
и даже литературе.
Слайд 17
Мобильная связь
В настоящее время на рынке мобильной связи
идет большая конкуренция среди операторов. Чем надежнее связь, чем
больше зона покрытия,
ем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу:
какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать
в определенном радиусе (например радиусе R=200 км?,
если известно. что радиус Земли равен 6380 км.)
Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB = OA + AB
OB = r + x
Используя теорему Пифагора, получим ответ. Ответ: 2,3 км.
Слайд 19
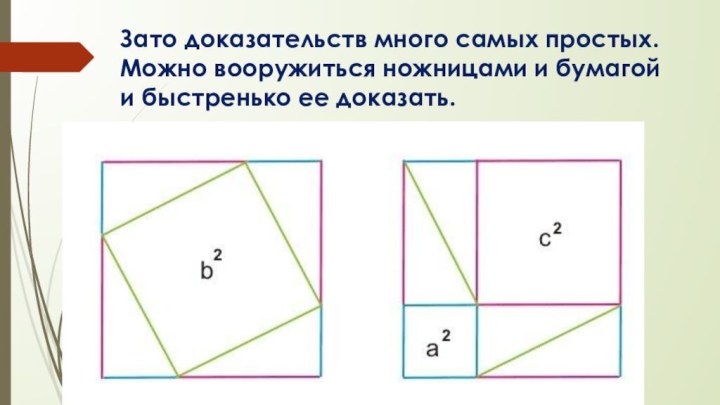
Зато доказательств много самых простых. Можно вооружиться ножницами
и бумагой и быстренько ее доказать.
Слайд 20
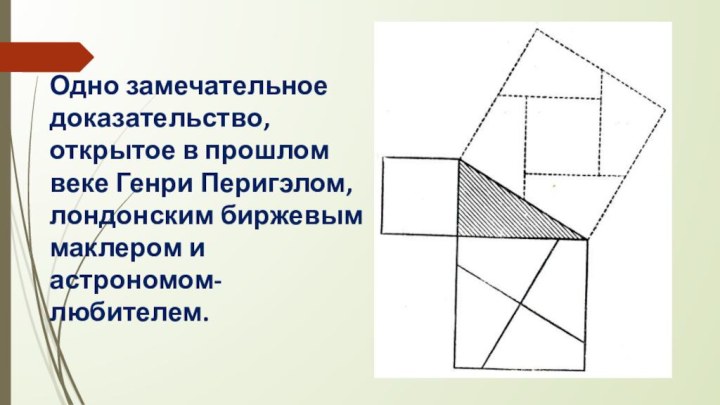
Одно замечательное доказательство, открытое в прошлом веке Генри
Перигэлом,
лондонским биржевым маклером и астрономом-любителем.
Слайд 21
Сегодня мы смогли заглянуть за пределы школьной программы
по математике и узнать не только те доказательства теоремы
Пифагора, которые приведены в учебниках «Геометрия 7-9» (Л.С. Атанасян, В.Н. Руденко) но и другие любопытные способы доказать знаменитую теорему. А также увидеть примеры, как теорема Пифагора может применяться в обычной жизни.








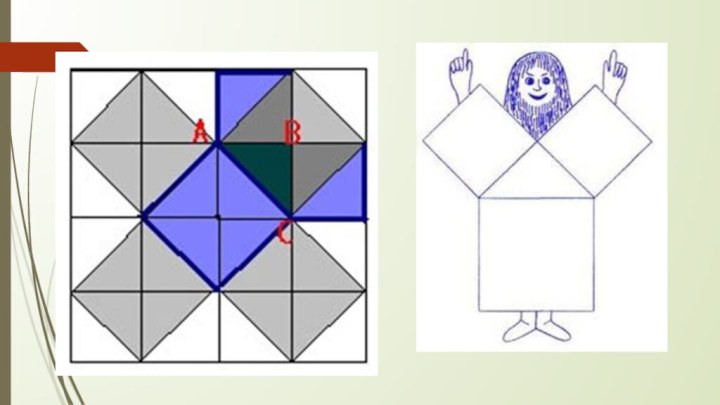

![Презентация к внеклассному мероприятию по геометрии Теорема Пифагора. (8 класс) Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]](/img/tmb/6/586691/6f714d229ab5330c02e319b9ecea6fe6-720x.jpg)