Слайд 2
Пифагор (570 – 490 года до н.э.) –
древнегреческий математик, мыслитель и философ.
Факты биографии Пифагора не известны
достоверно. О его жизненном пути можно судить лишь из произведений других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учеными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства.
Философия Пифагора, его образ жизни привлекли многих последователей, но у философа и ученого было и много противников.
Как математик Пифагор достиг больших успехов. Одна из самых известных геометрических теорем — теорема Пифагора, ему приписывают открытие и доказательство теоремы, создание таблицы Пифагора.
Слайд 3
Известны очень многие доказательства теоремы с разными математическими
методами, но одни из самых наглядных связаны с площадями.
Слайд 4
1. Построим квадрат, сторона которого равна сумме катетов
данного треугольника a+b. Площадь квадрата равна (a+b)^2
:
Слайд 5
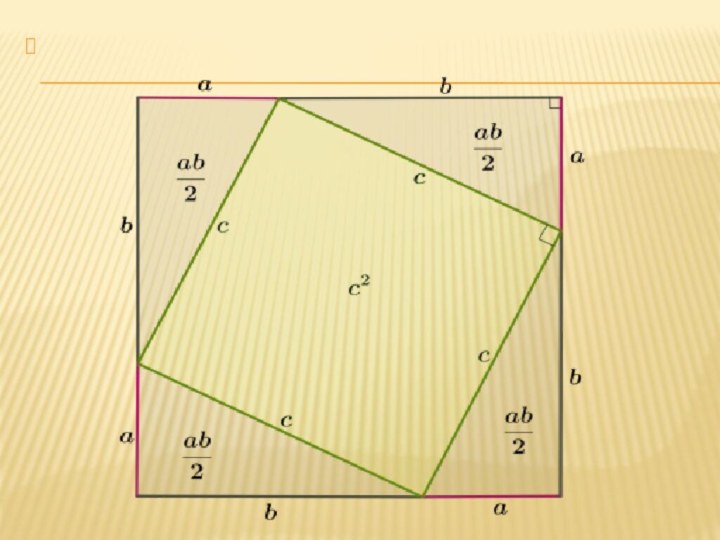
2. Если провести гипотенузы c, очевидно, что они образовали
квадрат внутри построенного квадрата.
Стороны четырёхугольника равны c, а углы — прямые,
так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами:
Слайд 7
3. На двух сторонах квадрата поменяем местами отрезки a и b,
при этом длина стороны квадрата не меняется.
Теперь площадь квадрата
можем сложить из двух площадей квадратов, образованных катетами a и b и двух площадей прямоугольников:
Слайд 8
4. Из этого следуют выводы:
4⋅ab/2=2ab и c^2=a^2+b^2, что и является
одним из доказательств теоремы Пифагора.
Обратная теорема используется как признак
прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным
Слайд 9
Пример:
Является ли треугольник со сторонами 5 см, 12 см и 13 см прямоугольным?
Выбираем большую сторону
и проверяем, выполняется ли теорема Пифагора:
13^2=12^2+5^2. Следовательно 169=144+25, значит,
этот треугольник прямоугольный.
Слайд 10
Задачи.
№1 Катеты прямоугольного треугольника равны 10 см и 24 см.
Найдите гипотенузу.
Решение:
По
теореме Пифагора:
C^2=a^2+b^2
C^2=10^2+24^2
C^2=676
c=26
Ответ: гипотенуза равна 26 см.
Слайд 11
Задачи.
№2 Диагонали ромба равны 16 см и 30 см.
Вычислите сторону ромба.
Решение:
Диагонали ромба пересекаются
под прямым углом, поэтому треугольник OCD —прямоугольный.
Диагонали точкой пересечения делятся пополам,
поэтому:
катет OC=30/2=15 см
катет OD=16/2=8 см
По т. Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
CD^2=OC^2+OD^2
CD^2=15^2+8^2
CD^2=289
CD=17
Ответ: сторона ромба равна 17
Слайд 12
Задачи.
№3 Возможно ли из бревна диаметром 20 см вырубить балку,
поперечное сечение которой — квадрат со стороной 16 см?
1. Если из
бревна диаметром 20 см вырубить балку, поперечное сечение которой — квадрат со стороной 16 см, то данный диаметр — диагональ квадрата.
2. Катеты треугольника ABC равны (как стороны квадрата), а диаметр AB — гипотенуза. По теореме Пифагора определим возможную длину стороны поперечного сечения балки.
Обозначим сторону за x и составим уравнение:
x^2+x^2=20^2
2x^2=20^2
x2=20^2/2
x=√20^2/2
x=20/√2 = 20√2/2
x≈14,1 см
Ответ Нет, такую балку вырубить нельзя