Презентация на тему Многоугольники. Решение задач

как частный вид многоугольника.
Ввести формулу суммы углов выпуклого многоугольника

www.konspekturoka.ru

EF, FK, KA - стороны многоугольника
A, B, C, D,

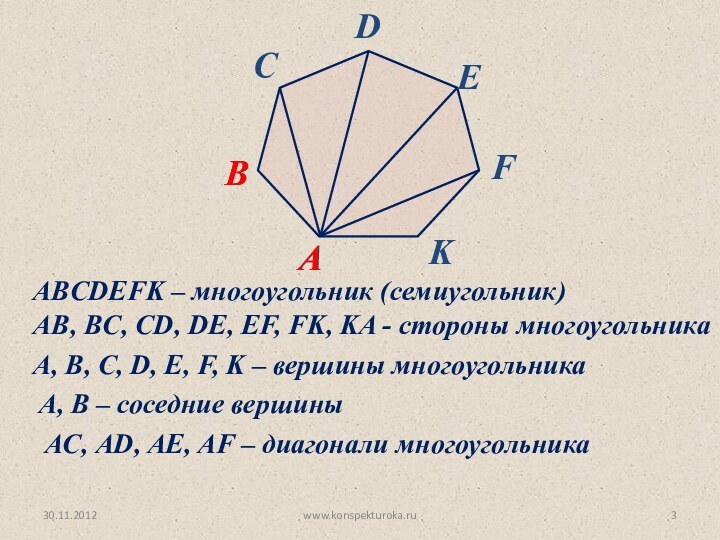
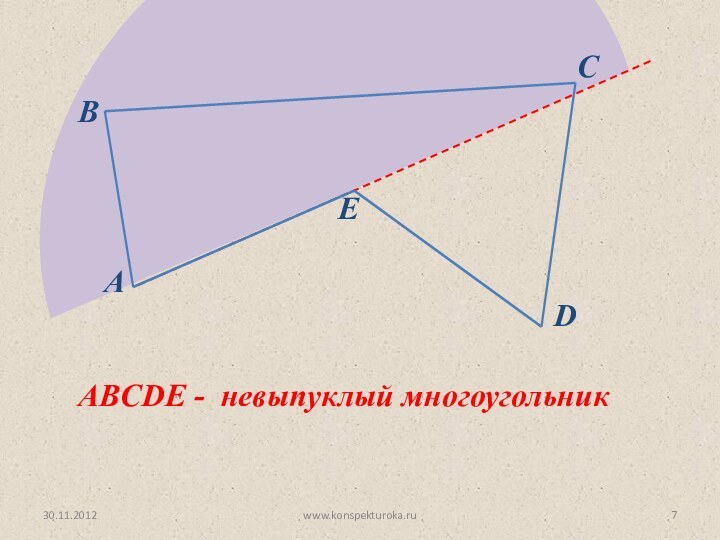
A, B – соседние вершины

AС, AD, AE, AF – диагонали многоугольника

сторону от каждой прямой, проходящей через
две его соседние

многоугольника
Найдем сумму всех углов многоугольника.
Для этого соединим вершину

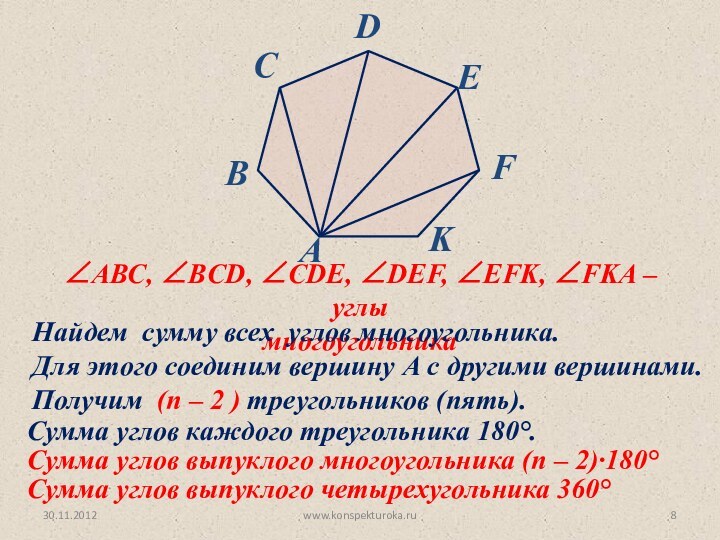
Сумма углов каждого треугольника 180°.

Сумма углов выпуклого многоугольника (п – 2)·180°

Сумма углов выпуклого четырехугольника 360°

которого равен 120°.
Решение
Так как сумма углов выпуклого многоугольника

То следовательно (п – 2) · 180° = 120° · п

Обозначим п – количество сторон многоугольника.

180° · п - 360° = 120° · п

60° · п = 360°

п = 360° : 60°

п = 6

Ответ: 6 сторон.

1

первая сторона больше второй на 8 см и на

2

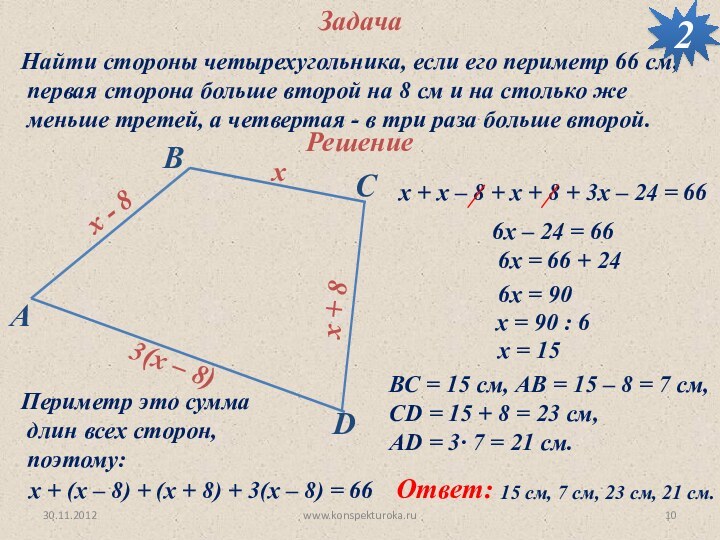
Решение

x

x - 8

x + 8

3(x – 8)

Периметр это сумма
длин всех сторон,
поэтому:

х + (x – 8) + (х + 8) + 3(х – 8) = 66

х + x – 8 + х + 8 + 3х – 24 = 66

6х – 24 = 66

6х = 66 + 24

6х = 90

х = 90 : 6

х = 15

ВС = 15 см, AB = 15 – 8 = 7 см,
CD = 15 + 8 = 23 cм,
AD = 3· 7 = 21 см.

Ответ:

15 см, 7 см, 23 cм, 21 см.

-?
Решение
По формуле о сумме углов
многоугольника

(п – 2)·180° = (4 – 2)·180° = 360°

По условию ∠А = ∠B =∠C =∠D,
следовательно ∠А = 360° : 4 = 90°

Ответ: 90°

- ?
Решение
∠А + ∠B + ∠C +

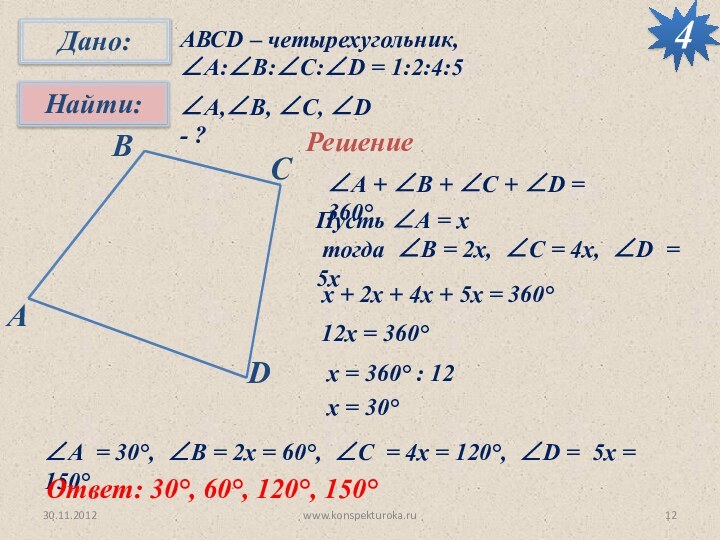
Пусть ∠А = х
тогда ∠B = 2х, ∠C = 4х, ∠D = 5х

х + 2х + 4х + 5х = 360°

12х = 360°

х = 360° : 12

х = 30°

∠А = 30°, ∠B = 2х = 60°, ∠C = 4х = 120°, ∠D = 5х = 150°

Ответ: 30°, 60°, 120°, 150°