- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение не геометрических задач геометрическим методом.
Содержание
- 2. СодержаниеСистемы уравнений.Тригонометрия.Взаимосвязанные иррациональности.Экстремумы.
- 3. Системы уравненийПрирода написана на языке математики.
- 4. Задача 1УсловиеДля положительных x, y, z из
- 5. Решениеy²/2+z²/2=25x²+xy+y²/2=169x²+xz+z²/2=144
- 6. РешениеSAOB=1/2*xy/√2*sin135°=1/4xySAOC=1/2*y/√2*z/√2 =1/4yzSBOC=1/2*x*z/√2*sin135°=1/4xzSABC=1/2*5*12=30Заметим, что значение выражения xy+yz+xz=120 равно учетверенной площади треугольника АВС. Итак, xy+yz+xz=120.Ответ:120.
- 7. ТригонометрияАрифметические знаки − это записанные геометрические фигуры,
- 8. Задача 2Докажите, что sin2α=2sinα*cosα(формула синуса двойного угла).
- 9. РешениеРассмотрим ∆АВС(АВ=ВС=1), угол АВС=2α, высоты AD и BE.AD=sin2α, AE=EC=sinα,BE=cosα/Так как ∆АВС~ ∆CAD, то AB/AC=BE/AD, т.е. 1/2sinα=cosα/sin2α,Sin2α=2sinα*cosα.
- 10. Взаимосвязанные иррациональностиМатематику уж затем учить следует, что
- 11. Задача 3Найдите наименьшее и наибольшее значения функции
- 12. Решение∆ADC (AC=2, CD=x, угол ACD=90°) и ∆BCD
- 13. Об экстремумахИ нет движенья – ни вперед,
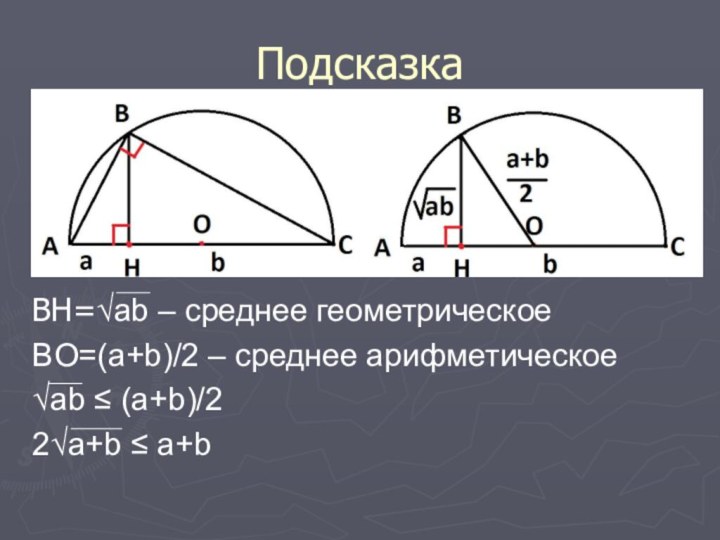
- 14. ПодсказкаBH=√ab – среднее геометрическоеBO=(a+b)/2 – среднее арифметическое √ab ≤ (a+b)/22√a+b ≤ a+b
- 15. Задача 4УсловиеПри каком значении аргумента x функция
- 16. Решение 5x²+4x+20 1
- 17. Задача 5Доказать, что:из всех прямоугольников с заданным
- 18. ДоказательствоПусть одна из сторон равна x, тогда
- 19. Доказательство2)Пусть сторона прямоугольника равна x, тогда при
- 20. Скачать презентацию
- 21. Похожие презентации
СодержаниеСистемы уравнений.Тригонометрия.Взаимосвязанные иррациональности.Экстремумы.

















Слайд 4
Задача 1
Условие
Для положительных x, y, z из условий
y²+z²=50,
x²+xy+y²/2=169,
x²+xz+z²/2=144,
не находя значений x, y, z вычислите значение
выражения xy+yz+xz.
Слайд 6
Решение
SAOB=1/2*xy/√2*sin135°=1/4xy
SAOC=1/2*y/√2*z/√2 =1/4yz
SBOC=1/2*x*z/√2*sin135°=1/4xz
SABC=1/2*5*12=30
Заметим, что значение выражения xy+yz+xz=120 равно учетверенной
площади треугольника АВС. Итак, xy+yz+xz=120.
Ответ:120.
Слайд 7
Тригонометрия
Арифметические знаки − это записанные геометрические фигуры, а
геометрические фигуры − это нарисованные фигуры.
Д.Гильберт
Слайд 9
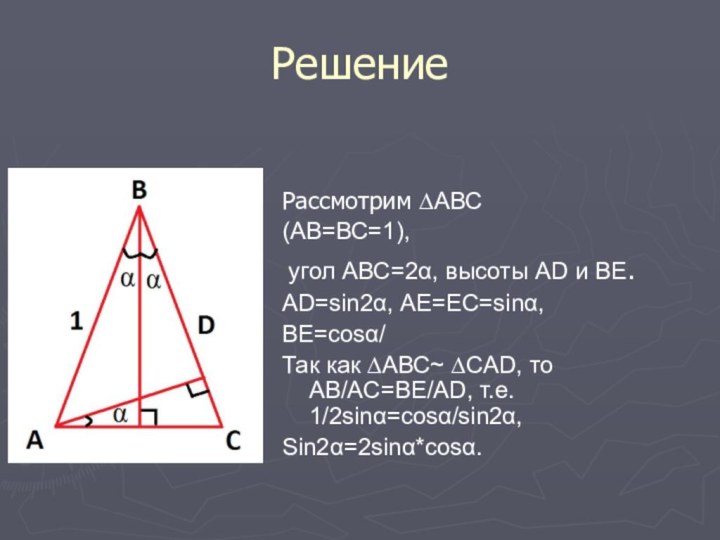
Решение
Рассмотрим ∆АВС
(АВ=ВС=1),
угол АВС=2α, высоты AD и BE.
AD=sin2α,
AE=EC=sinα,
BE=cosα/
Так как ∆АВС~ ∆CAD, то AB/AC=BE/AD, т.е. 1/2sinα=cosα/sin2α,
Sin2α=2sinα*cosα.
Слайд 10
Взаимосвязанные иррациональности
Математику уж затем учить следует, что она
ум в порядок приводит.
М.Ломоносов
Слайд 11
Задача 3
Найдите наименьшее и наибольшее значения функции
f(x)=√x²+4
+√x²-3x√3+9
В природе все подлежит измерению, все может быть сосчитано.
Н.Лобачевский
Слайд 12
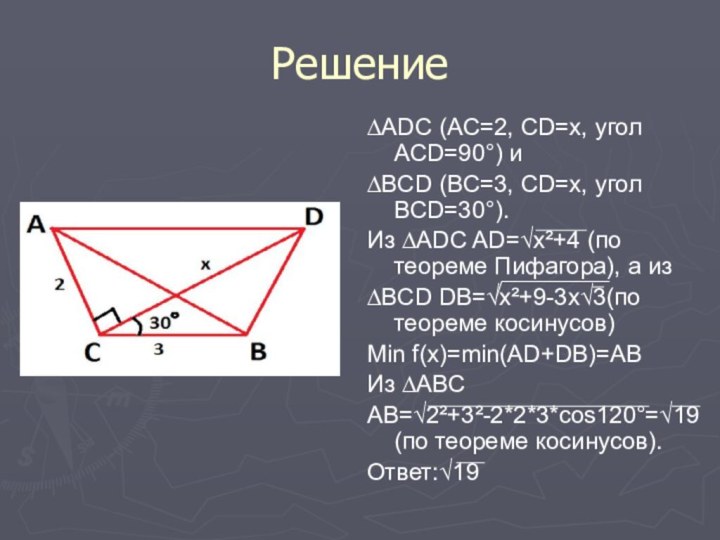
Решение
∆ADC (AC=2, CD=x, угол ACD=90°) и
∆BCD (BC=3,
CD=x, угол BCD=30°).
Из ∆ADC AD=√x²+4 (по теореме Пифагора), а
из ∆BCD DB=√x²+9-3x√3(по теореме косинусов)
Min f(x)=min(AD+DB)=AB
Из ∆ABC
AB=√2²+3²-2*2*3*cos120°=√19 (по теореме косинусов).
Ответ:√19
Слайд 14
Подсказка
BH=√ab – среднее геометрическое
BO=(a+b)/2 – среднее арифметическое
√ab
≤ (a+b)/2
2√a+b ≤ a+b
Слайд 15
Задача 4
Условие
При каком значении аргумента x функция
f(x)
принимает наименьшее значение? Вычислите min f(x).
5x²+4x+20f(x)= 2x , x>0.
Слайд 16
Решение
5x²+4x+20 1
2x
2 1 1 20
2 2 x
5x²+4x+20
2x
X=2
Ответ: min f(x)=f(2)=12.
=
(
5x+
20
x
)
+2
(5x+
20
x
)
+2
≥
*2
√
5x*
+2
=12
Слайд 17
Задача 5
Доказать, что:
из всех прямоугольников с заданным периметром
наибольшую площадь имеет квадрат;
из всех прямоугольников с заданной площадью
наименьший периметр имеет квадрат.
Слайд 18
Доказательство
Пусть одна из сторон равна x, тогда при
заданном периметре P=4a вторая сторона равна 2a-x.
S(x)=(2a-x)x
(2a-x)x ≤ , ((2a-x+x)/2)²=a²(2a-x)x=a² <=> x²-2xa+a²=0 <=> x=a
Max S(x)=a² при x=a.
2a-x-x
2
( )
2
Слайд 19
Доказательство
2)Пусть сторона прямоугольника равна x, тогда при заданной
площади S(x)=a² другая его сторона равна a²/x.
P(x)=2(a²/x+x)
2(a²/x+x) ≥ 2*2√x* , 2*2√x* =4a2(x+a²/x)=4a <=> x²-4ax+a²=0 <=> x=a
Min P(x)=4a при x=a.
Что и требовалось доказать.
a²
x
a²
x