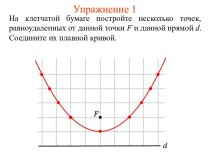
V=πR2H
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Объемы тел
Содержание
- 3.
- 4.
- 5.
- 6.
- 7. Цилиндр и конус имеют общее основание и
- 8. Цилиндр и конус имеют общие основание и
- 9. Объем конуса равен 16. Через середину высоты
- 10. Во сколько раз уменьшится объем конуса, если
- 11. Во сколько раз увеличится объем конуса, если
- 12. В сосуде, имеющем форму конуса, уровень
- 13. Прямоугольный параллелепипед описан около цилиндра, радиус основания
- 14. В куб вписан шар радиуса 1. Найдите
- 15. Во сколько раз объем конуса, описанного около
- 16. Объём тетраэдра равен 19. Найдите объём многогранника,
- 17. Цилиндр описан около шара. Объем цилиндра равен
- 18. Цилиндр описан около шара. Объем шара равен
- 19. Найдите объем многогранника, вершинами которого являются точки
- 20. Найдите объем многогранника, вершинами которого являются точки
- 21. В сосуд, имеющий форму правильной треугольной призмы,
- 22. В сосуд, имеющий форму правильной треугольной призмы,
- 23. Найдите объем многогранника, вершинами которого являются точки
- 24. Найдите объем многогранника, вершинами которого являются точки
- 25. Во сколько раз увеличится объем правильного
- 26. Во сколько раз увеличится объем пирамиды,
- 27. Найдите объем V части цилиндра, изображенной на
- 28. Найдите объем V части цилиндра, изображенной на
- 29. 16-1.В правильной треугольной пирамиде SABC с основанием
- 30.
- 31. Список используемой литературы и ресурсов :1. ЕГЭ-2015.Математика.50
- 32. Скачать презентацию
- 33. Похожие презентации
V=πR2H

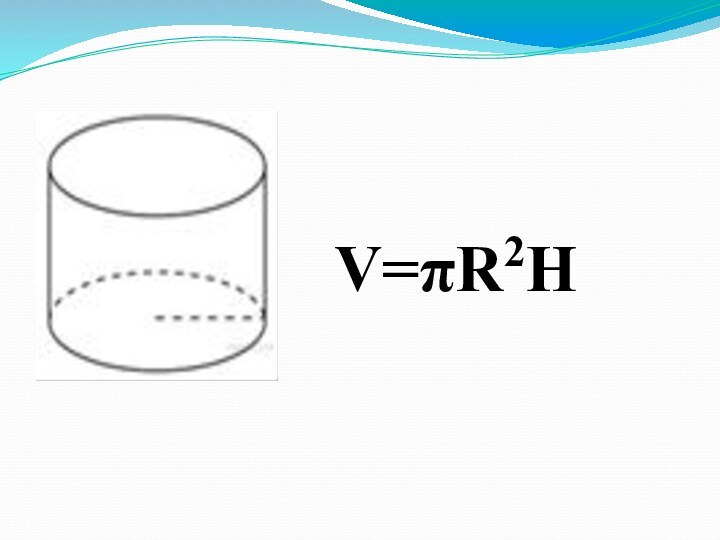
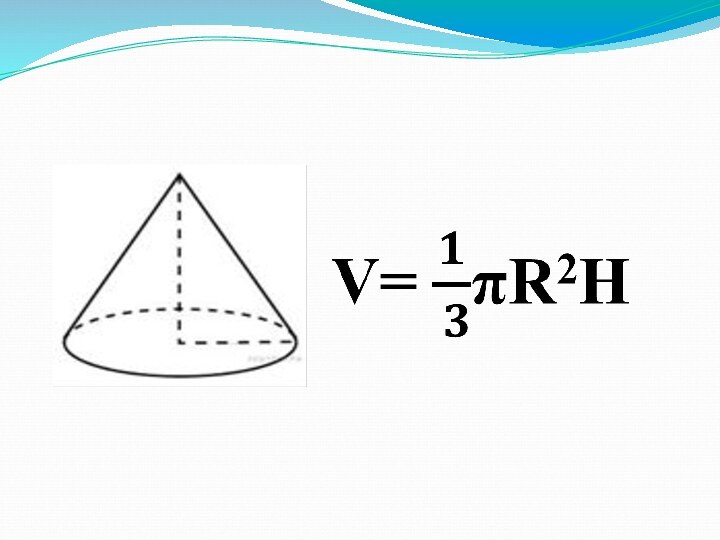
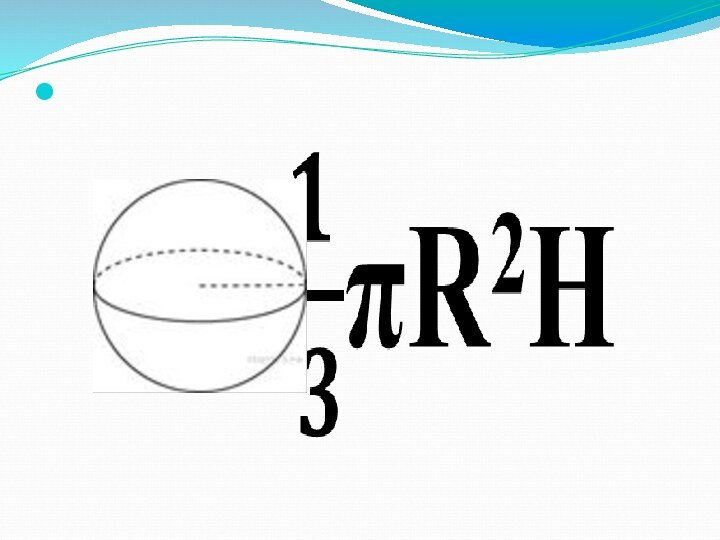
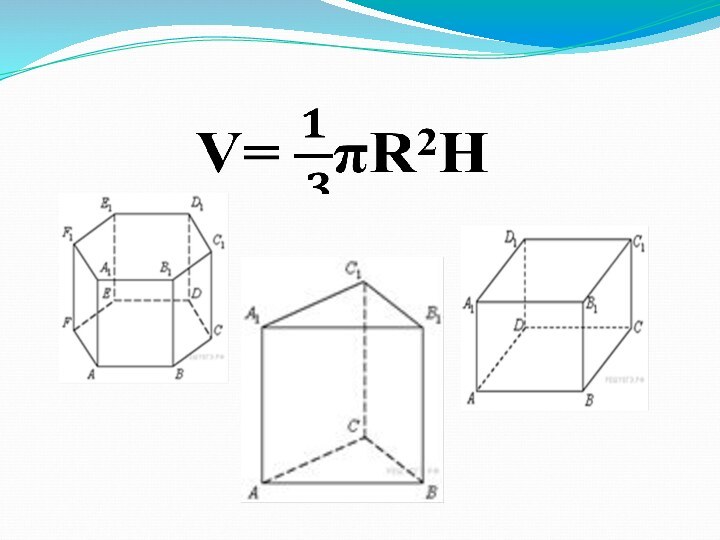
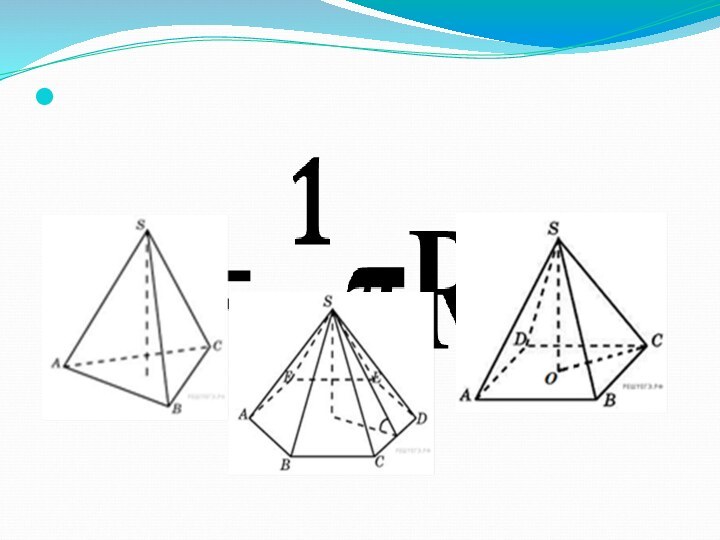


























Слайд 7 Цилиндр и конус имеют общее основание и общую
высоту. Вычислите объём цилиндра, если объём конуса равен 25.
Ответ:
75Слайд 8 Цилиндр и конус имеют общие основание и высоту.
Найдите объём конуса, если объём
цилиндра равен 150.Ответ:50
Слайд 9 Объем конуса равен 16. Через середину высоты параллельно
основанию конуса проведено сечение, которое является основанием меньшего конуса
с той же вершиной. Найдите объем меньшего конуса.Решение.
Больший конус подобен меньшему с коэффициентом 2. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.
Ответ: 8
Слайд 10 Во сколько раз уменьшится объем конуса, если его
высоту уменьшить в 3 раза?
Решение.
Объем конуса равен
где S
– площадь основания, а h – высота конуса. При уменьшении высоты в 3 раза объем конуса также уменьшится в 3 раза.Ответ: 3.
,
Слайд 11 Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 1,5 раза?
Решение.
Объем конуса равен
где – площадь основания, – высота конуса, а – радиус основания. При увеличении радиуса основания в 1,5 раза объем конуса увеличится в 2,25 раза.
Ответ: 2,25.
Слайд 12 В сосуде, имеющем форму конуса, уровень жидкости
достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров
жидкости нужно долить, чтобы полностью наполнить сосуд?Решение.
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.
Ответ: 490.
Слайд 13 Прямоугольный параллелепипед описан около цилиндра, радиус основания и
высота которого равны 1. Найдите объем параллелепипеда.
Решение.
Высота параллелепипеда
равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен Ответ: 4.
.
Слайд 14 В куб вписан шар радиуса 1. Найдите объем
куба.
Решение.
Ребро куба равно диаметру вписанного в него шара, а
объем куба равен кубу его ребра. Отсюда имеем:Ответ: 8.
.
Слайд 15 Во сколько раз объем конуса, описанного около правильной
четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Решение.
Объемы данных конусов соотносятся как площади их оснований, и, следовательно, как квадраты их диаметров. Диаметр вписанного конуса равен стороне квадрата, диаметр описанного – диагонали квадрата, длина которой равна длины стороны. Поэтому объем описанного конуса в 2 раза больше объема вписанного.
Ответ: 2.
Слайд 16 Объём тетраэдра равен 19. Найдите объём многогранника, вершинами
которого являются середины рёбер данного тетраэдра.
Решение.
Объем данного многогранника равен
разности объемов исходного тетраэдра и четырех тетраэдров, одни из вершин которых совпадают с вершинами исходного: Ответ: 9,5.
.
Слайд 17 Цилиндр описан около шара. Объем цилиндра равен 33.
Найдите объем шара.
Решение.
Выразим из формулы для объёма цилиндра
и подставим в формулу для объёма шараОтвет: 22.
,
Слайд 18 Цилиндр описан около шара. Объем шара равен 24.
Найдите объем цилиндра.
Решение.
Объем цилиндра равен произведению площади основания на
высоту. Площадь основания цилиндра равна площади большого круга вписанного шара, а высота цилиндра равна диаметру вписанного шара. ПоэтомуОтвет: 36.
Слайд 19 Найдите объем многогранника, вершинами которого являются точки A,
B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=4,
AD=3 , AA1=4.Решение.
Площадь основания пирамиды в два раза меньше площади основания параллелепипеда, а высота у них общая. Поэтому
Ответ: 8.
Слайд 20 Найдите объем многогранника, вершинами которого являются точки A1,B,C,
C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=4, AD=3,
AA1=4.Решение.
Основанием пирамиды, объем которой нужно найти, является боковая грань параллелепипеда, а ее высотой является ребро A1B1. Поэтому
Ответ: 16.
Слайд 21 В сосуд, имеющий форму правильной треугольной призмы, налили
2300 см3воды и погрузили в воду деталь. При этом уровень
воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали.Решение.
Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 2/25 исходного объёма:
Ответ: 184.
Слайд 22 В сосуд, имеющий форму правильной треугольной призмы, налили
воду. Уровень воды достигает 80 см. На какой высоте
будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.Решение.
Объем призмы равен произведению площади ее основания на высоту и выражается через сторону основания а и высоту Н формулой
Поэтому , а значит, при увеличении стороны а в 4 раза знаменатель увеличится в 16 раз, то есть высота уменьшится в 16 раз и будет равна 5 см.
Ответ: 5.
Слайд 23 Найдите объем многогранника, вершинами которого являются точки A,
B,C, D,E, F,A1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания
которой равна 4, а боковое ребро равно 3.Решение.
Основание пирамиды такое же, как основание правильной шестиугольной призмы, и высота у них общая. Поэтому
Ответ: 4.
Слайд 24 Найдите объем многогранника, вершинами которого являются точки A,
B, C, B1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания
которой равна 6, а боковое ребро равно 3.Решение.
Площадь основания треугольной пирамиды равна одной шестой площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому
Ответ: 1.
Слайд 25 Во сколько раз увеличится объем правильного тетраэдра,
если все его ребра увеличить в два раза?
Решение.
Объёмы
подобных тел относятся как куб коэффициента подобия. Поэтому если все ребра увеличить в 2 раза, объём увеличится в 8 раз.Это же следует из формулы для объёма правильного тетраэдра
, где a — длина его ребра.
Ответ: 8.
Слайд 26 Во сколько раз увеличится объем пирамиды, если
ее высоту увеличить в четыре раза?
Решение.
Объем пирамиды равен
где S – площадь основания, а h – высота пирамиды. При увеличении высоты в 4 раза объем пирамиды также увеличится в 4 раза.
Ответ: 4.
Слайд 27 Найдите объем V части цилиндра, изображенной на рисунке.
В ответе укажите V/π.
Решение.
Объем данной части цилиндра равен
Ответ: 144.
Слайд 28 Найдите объем V части цилиндра, изображенной на рисунке.
В ответе укажите V/π .
Решение.
Объем данной части цилиндра равен
Ответ: 937,5.
Слайд 29 16-1.В правильной треугольной пирамиде SABC с основанием ABC
боковое ребро равно 5, а сторона основания равна 6.
Найдите расстояние от вершины A до плоскости SBC.Решение.
Пусть SO – высота пирамиды. Тогда
Пусть V – объём пирамиды, тогда
С другой стороны, где h – искомое расстояние.
В треугольнике SBC высота SM равна
Площадь треугольника SBC равна
Получаем, что
Ответ:
Слайд 31
Список используемой литературы и ресурсов :
1. ЕГЭ-2015.Математика.50 вариантов
типовых тестовых заданий / под ред. И.В.Ященко. – М.:
Издательство «Экзамен», 20153.mathege.ru
4.reshuege.ru