- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Площади фигур (9 класс)
Содержание
- 2. Тема. Площа трикутникаМета. Систематизувати і узагальнити знання,
- 3. Розвивати логічне мислення,пам'ять, увагу, обчислювальну техніку. Виховувати
- 4. Обладнання: картки з задачами; картки самоконтролю; таблиці
- 5. Очікувані результати У процесі уроку учні зможуть: повторити і
- 6. ЕпіграфУ математиків існує своя мова – це
- 10. Задача 2 група
- 11. Задача 3 група «Маляри»Витрати емалевої
- 12. Задача 4
- 13. ІІІ. Мотивація навчання. Виникає запитання:Чи потрібні знання
- 14. ІV. Записуємо число та тему
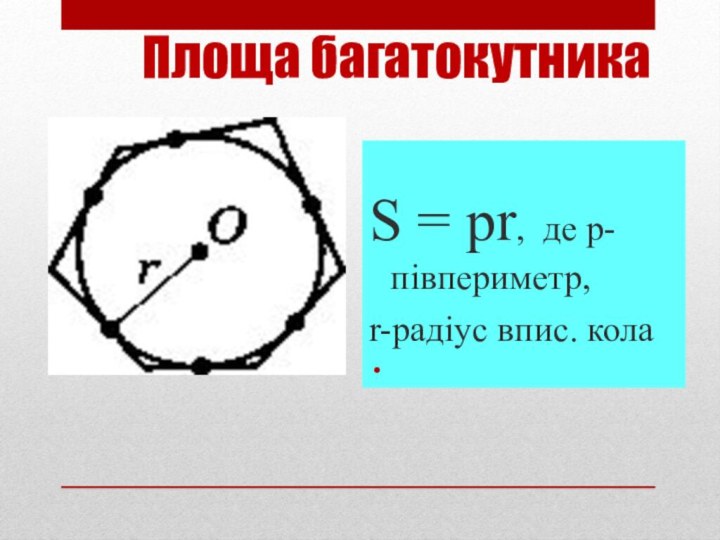
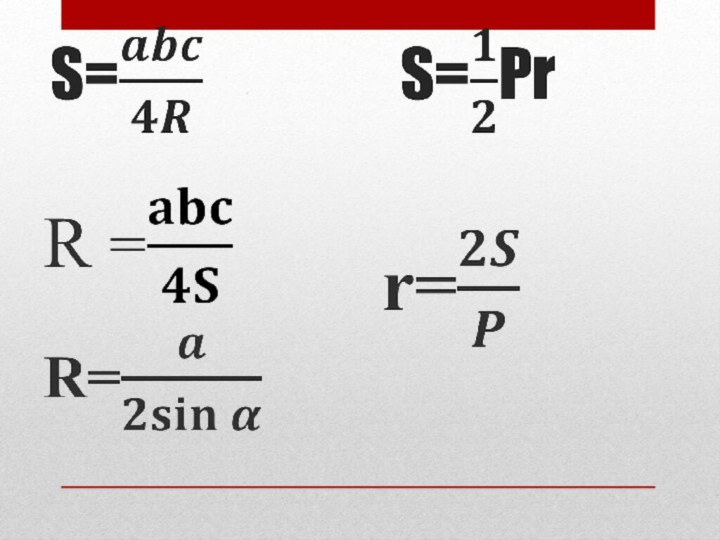
- 16. Площа багатокутника S = рr, де р- півпериметр,r-радіус впис. кола
- 17. Площа чотирикутникаЧотирикутником називається багатокутник, який має чотири вершини і чотири кути.d2d1αназад
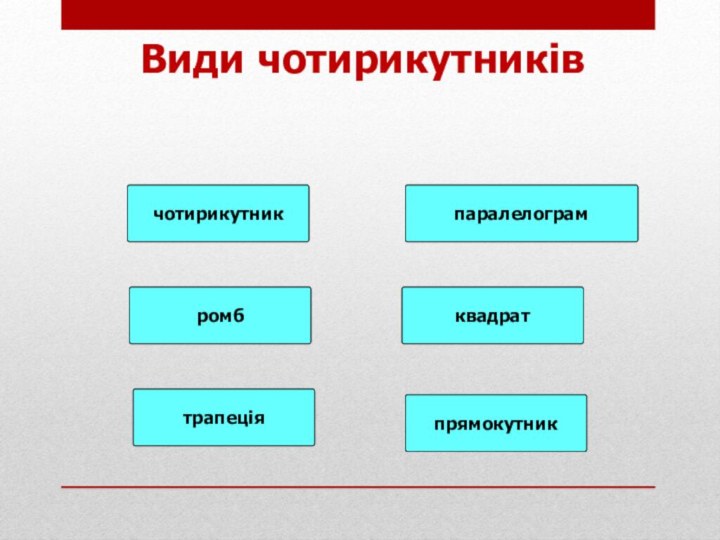
- 18. чотирикутникпаралелограмромбквадраттрапеціяпрямокутникВиди чотирикутників
- 19. Площа паралелограмаПаралелограм – це чотирикутник, у якого протилежні сторони паралельні, тобто лежать на паралельних прямих haaназад
- 20. Площа паралелограмаba
- 21. Площа паралелограмаd1d2α
- 22. Площа ромба
- 23. Площа прямокутника S= аb
- 24. Площа квадратаКвадрат – це прямокутник, у якого всі сторони рівні.
- 25. Площа трапеції
- 26. Формули площ трикутниківahaab
- 27. Формула Геронаbac
- 28. Прямокутний трикутник А
- 29. Правильний трикутник aaa
- 30. Площа трикутника
- 31. Площа трикутникаS = pr р- півпериметр трикутника, r - радіус вписаного кола
- 32. Ми площу трикутника запишемо у довгий ряд, помноживши синуси на два, на «ер-квадрат".
- 33. А-в-квадраті" ми поділим на два синуса своїх, а потім перемножим на два синуса других.
- 35. VІ. Сторінки з минулого ПОВІДОМЛЕННЯ 3. Формула ГЕРОНАПовідомлення4 Архімед-вершина наукової думки стародавнього світу
- 36. Формула Герона Формула площі трикутника, для доведення
- 37. Герон розглядав трикутники з цілочисельними сторонами, площі
- 38. Існують формули ,аналогічні формулі Герона , для
- 39. АРХІМЕД (287—212 p. до н. е.) Народився
- 40. Наукова діяльність Архімеда була пов'язана з життєвими
- 41. VІ. РОЗВ'ЯЗУВАННЯ ВПРАВ ЗА МАЛЮНКОМ 1)
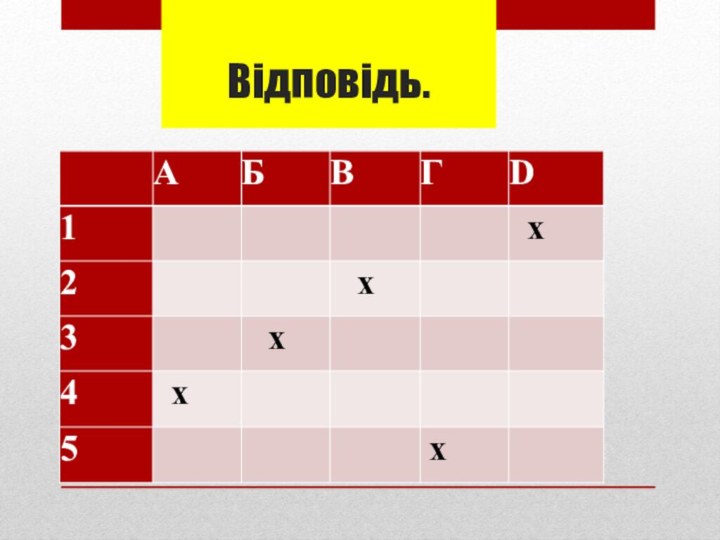
- 42. Відповідь.
- 43. VІ. Робота в парах. Трикутник
- 45. Задача2. У трикутнику зі сторонами
- 46. VІІІ. Самостійна робота
- 48. За результатами прочитати слово
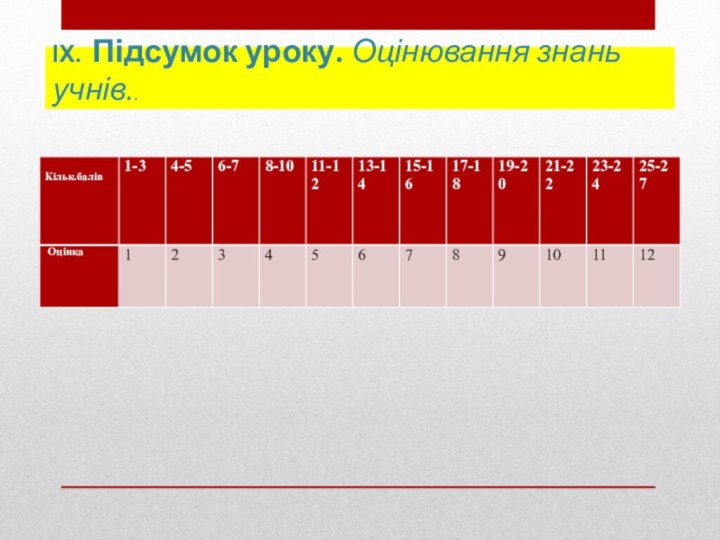
- 49. ІХ. Підсумок уроку. Оцінювання знань учнів..
- 50. Відповіді
- 51. Інтерактивна вправа «Результат» 1).Інтерактивна вправа
- 52. Рефлексія Чи
- 53. Х. Домашнє завдання. ПАРАГРАФ
- 54. Бажаю успіхів!
- 55. Дану презентацію рекомендуємо використовувати при узагальненні вивчення
- 56. Площа— величина, що визначає розмір поверхні, одна
- 57. Проста геометрична фігура Геометрична фігура називається
- 58. ПЛОЩА – це додатна величина, числове значення
- 59. За одиницю вимірювання площі беруть площу
- 60. чотирикутникпаралелограмромбквадраттрапеціяпрямокутник
- 61. Задачі на знаходження площі фігур
- 62. Задача 1 Одне вікно має розміри 1,
- 63. Задача 4 Підлога майстерні має форму
- 64. Скачать презентацию
- 65. Похожие презентации
Тема. Площа трикутникаМета. Систематизувати і узагальнити знання, уміння та навички учнів із теми «Площа трикутників». Закріпити навички використання формул при розв’язуванні задач на знаходження площ трикутника і чотирикутника.



























































Слайд 3
Розвивати логічне мислення,пам'ять, увагу, обчислювальну техніку.
Виховувати старанність,
почуття колективізму, відповідальність за себе та своїх товаришів, бажання
вчитися, критичне мислення.Тип уроку. Урок узагальнення і систематизації знань, умінь та навичків.
Слайд 4
Обладнання:
картки з задачами;
картки самоконтролю;
таблиці з
формулами;
презентація «Площа трикутника»;
повідомлення: «Формула Герона»; «Застосування площ
фігур у житті»; «Архімед-вершина наукової думки стародавнього світу».
Слайд 5
Очікувані результати
У процесі уроку учні зможуть:
повторити і закріпити
знання формул з теми;
удосконалити свої вміння та навички
знаходити площі фігур;поглибити свої знання історичним матеріалом;
розвивати техніку обчислення, просторову уяву.
Слайд 7
Девіз уроку
Скажи мені – я забуду.
Покажи мені –
я запам'ятаю.
Залучи мене - я навчусь.
Cхідна приказка
Слайд 8
Хід уроку І. Організаційний момент ІІ. Перевірка
домашнього завданняУчні розділенні на 4 групи. Кожна група працювала над розв’занням практичної задачі і звітує про виконання.
Слайд 9
Задача 1
група «Столяри»
Скільки дощок довжиною
4,5 м і шириною 0,125 м потрібно для настилання підлоги, довжина якої 8,2м, а ширина –6м?
Слайд 10 Задача 2 група «
Постачальники»
У кімнаті довжиною 8,2 м і шириною 6 м
потрібно зробити паркетну підлогу з квадратних дощечок, сторона яких 200 мм.Скільки дощечок
піде на підлогу?
Слайд 11
Задача 3
група «Маляри»
Витрати емалевої фарби ПФ-115
на одношарове покриття становить
180 г на 1 кв.м.
Чи вистачить 9кг емалі,щоб
пофарбувати
підлогу класної кімнати?
Слайд 12
Задача 4
група « Муляри»
Скільки рулонів шпалери розміром
0,5х 10 кв.м. потрібно придбати,
щоб обклеїти у
класі нижню частину стіни, висота якої 1,2м.Слайд 13 ІІІ. Мотивація навчання. Виникає запитання:Чи потрібні знання і
вміння з теми «Площа багатокутників»?
Коротке повідомлення1: «Застосування площ
фігур ужитті»Учитись нелегко буває,
Та наука завжди хороша.
Кожна в світі людина знає
З геометрії знання — найцінніша ноша.
Слайд 14
ІV. Записуємо число та тему уроку.
Шосте
листопада
Класна робота
Площа трикутника
V. Узагальнення і систематизація
знань учнів.Повідомлення 2.
Презентація «Площа трикутника та чотирикутника»
Учні у цей час заповнюють таблицю «Площа Фігур»
Слайд 17
Площа чотирикутника
Чотирикутником називається багатокутник, який має чотири вершини
і чотири кути.
d2
d1
α
назад
Слайд 19
Площа паралелограма
Паралелограм – це чотирикутник, у якого протилежні
сторони паралельні, тобто лежать на паралельних прямих
ha
a
назад
Слайд 35
VІ. Сторінки з минулого
ПОВІДОМЛЕННЯ 3.
Формула
ГЕРОНА
Повідомлення4
Архімед-вершина наукової думки
стародавнього світу
Слайд 36
Формула Герона
Формула площі трикутника, для доведення якої можна
використати тригонометричні функції, була наведена давньогрецьким математиком Героном Александрійським
(прибл. І ст. до н. е.) і отримала його ім’я. Тільки у ХХ ст. з’ясувалося, що раніше за Герона цю формулу винайшов Архімед.
Слайд 37
Герон розглядав трикутники з цілочисельними сторонами, площі яких
є цілими числами. Такі трикутники називають героновими. Наприклад, це
трикутники зі сторонами 13, 14, 15 або 51, 52, 53.
Герон півпериметр
під корінь затягнув,
Три рази перемножив
і площу получив.
Слайд 38 Існують формули ,аналогічні формулі Герона , для знаходження
площі чотирикутника.
Наприклад, площу вписаного чотирикутника
знаходять за формулою.
Якщо
ж чотирикутник і вписаний, і описаний одночасно, то його площу знаходять за простою формулою:
Слайд 39
АРХІМЕД (287—212 p. до н. е.)
Народився Архімед близько
287 року до н. е. в Сіракузах на острові
Сіцілія. Здобувши освітуу свого батька — астронома і математика Фідія.
Архімед переїхав до Олександрії удосконалювати свої знання з математики й астрономії. Тут він зблизився з учнями Евкліда: математиком Ератосфеном, астрономом Кононом і Досіфеєм. Повернувшись до Сіракуз, Архімед підтримував зв'язки з цими вченими. Частина його праць дійшла до нас у вигляді листів до видатних математиків.
Слайд 40 Наукова діяльність Архімеда була пов'язана з життєвими потребами
його батьківщини. Учений проводив дослідження у галузі математики, фізики,
механіки, астрономії. За переказами, він так захоплювався наукою, що забував навіть про їжу. Архімед був також видатним інженером-винахідником і брав безпосередню участь у підготовці оборонних споруд.!Слайд 41 VІ. РОЗВ'ЯЗУВАННЯ ВПРАВ ЗА МАЛЮНКОМ 1) Установіть
відповідність між фігурою (1-4) та її площею (А-Д).
Слайд 43 VІ. Робота в парах. Трикутник перегніть
по прямій, яка поділить його на
два рівновеликих трикутника.
1.
Чи правда, що медіана трикутника ділить його на два трикутники з однаковою площею? Чому? 2. Чи правда, що висота трикутника ділить його на два трикутники з однаковою площею? Чому?
3. Чи правда, що висота рівнобедреного трикутника ділить його на два трикутники з однаковою площею? Чому?
4..Чи правда, що висота рівносторонього трикутника ділить його на два трикутники з однаковою площею? Чому?
Слайд 45 Задача2. У трикутнику зі сторонами 8см і 4см
проведені висоти до цих сторін. Висота, проведена до сторони
8см, дорівнює 3см. Чому дорівнює висота, проведена до сторони 4см?
Слайд 51
Інтерактивна вправа «Результат»
1).Інтерактивна вправа «Результат»
Сьогодні на
уроці я повторив…
Сьогодні я зрозумів…
Я дізнався …
Найважчим для
мене було…
Слайд 53
Х. Домашнє завдання.
ПАРАГРАФ 8.
Повт.формули площі трик. і чотир. К.Р.№2
(вар.4 ) задачі №:7-9
4- 6
1-3
Слайд 55 Дану презентацію рекомендуємо використовувати при узагальненні вивчення теми
“Площі фігур”
Вона розбита на дві теми:
“Площа чотирикутника” і
“Площа трикутника”
Слайд 56 Площа— величина, що визначає розмір поверхні, одна з
основних властивостей геометричних фігур. Історично, обчислення площі називалося квадратурою. Фігура,
що має площу, називається квадрованою. Площу нескладних геометричних фігур визначають, підраховуючи кількість одиничних квадратів, якими фігури можна покрити. Площу заведено позначати великою латинською літерою S
Слайд 57
Проста геометрична фігура
Геометрична фігура називається простою, якщо її
можна розбити на скінченну кількість плоских трикутників
Слайд 58 ПЛОЩА – це додатна величина, числове значення якої
має такі властивості:
Рівні фігури мають рівні площі.
Якщо фігура розбивається
на частини, що є простими фігурами, то площа цієї фігури дорівнює сумі площ її частин.Площа квадрата із стороною, що дорівнює одиниці вимірювання, дорівнює одиниці.
Слайд 59
За одиницю вимірювання площі беруть площу квадрата,
сторона якого дорівнює одиниці довжини
1см
1дм1см2 1дм2
Слайд 62
Задача 1
Одне вікно має розміри 1, 3
х 1,1 м. Обчисліть скільки скла піде для скління
250 таких вікон? На обріз склайде 8% його загальної площі.