Слайд 2
Задачи на построение
Окружность
Предложение, в котором разъясняется смысл того
или иного выражения или названия, называется определением. Мы уже
встречались с определениями, например с определением угла, смежных углов, равнобедренного треугольника и т. д. Дадим определение еще одной геометрической фигуры — окружности.
Определение
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной
точки.
Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности. Из определения окружности следует, что все радиусы имеют одну и ту же длину.
Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Слайд 3
На рисунке отрезки АВ и ЕF — хорды
окружности, отрезок СВ — диаметр окружности. Очевидно, диаметр окружности
в два раза больше ее радиуса.
Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. На рисунке АLВ и АМВ — дуги, ограниченные точками А и В.
Слайд 4
Построения циркулем и линейкой
Оказывается, что многие построения можно
выполнить с помощью только циркуля и линейки без масштабных
делений. Поэтому в геометрии специально выделяют те задачи на построение, которые решаются с помощью только этих двух инструментов.
Что можно делать с их помощью? Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки. С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. Выполняя эти несложные операции, мы сможем решить много интересных задач на построение:
построить угол, равный данному;
через данную точку провести перпендикулярную к данной прямую прямой;
разделить данный отрезок пополам и другие задачи.
Слайд 5
Задача. На данном луче от его начала отложить
отрезок, равный данному.
Решение
Изобразим фигуры, данные в условии задачи: луч
ОС и отрезок АВ. Затем циркулем построим окружность радиуса АВ с центром О. Эта окружность пересечет луч ОС в некоторой точке В. Отрезок ОВ — искомый.
Слайд 6
Задача
Отложить от данного луча угол, равный данному.
Решение
Данный угол
с вершиной А и луч ОМ изображены на рисунке.
Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ.
Проведем окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С.
Слайд 7
Затем проведем окружность того же радиуса с центром
в начале данного луча ОМ. Она пересекает луч в
точке D.
После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ — искомый.
Слайд 8
Рассмотрим треугольники АВС и ОDЕ. Отрезки АВ и
АС являются радиусами окружности с центром А, а отрезки
ОD и ОЕ — радиусами окружности с центром О.
Так как по построению эти окружности имеют равные радиусы, то АВ = ОD, АС = ОЕ. Также по построению ВС = DЕ.
Следовательно, ∆АВС = ∆ ОDЕ по трем сторонам. Поэтому ∟DОЕ = ∟ ВАС, т. е. построенный угол МОЕ равен данному углу А.
Слайд 9
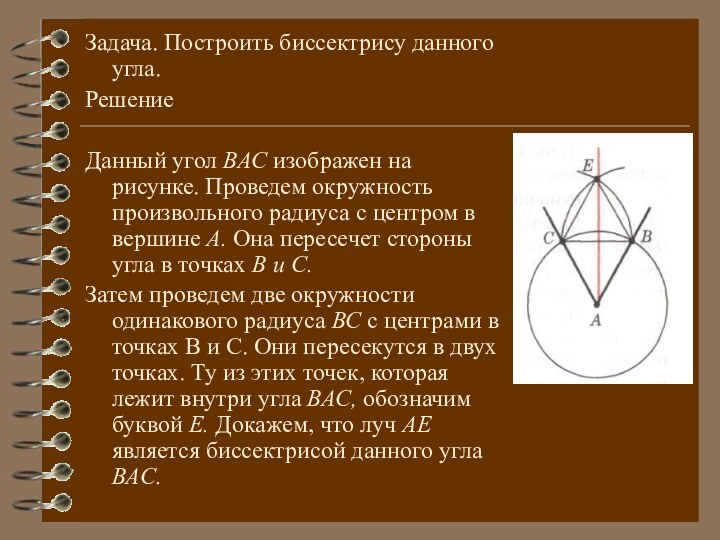
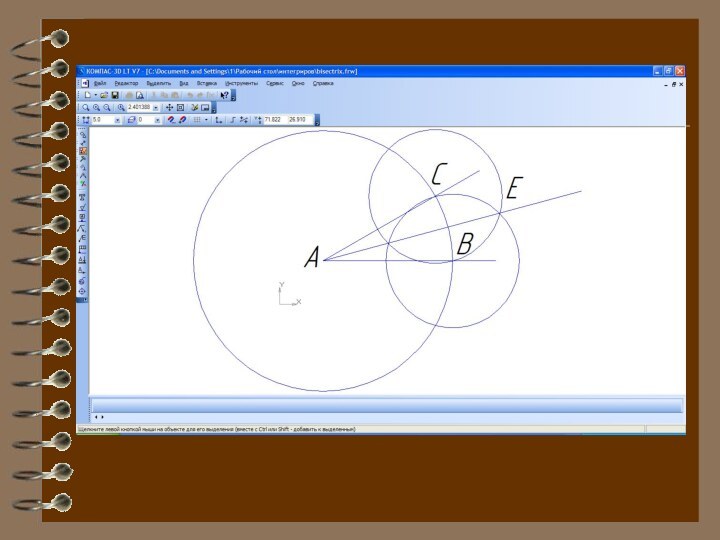
Задача. Построить биссектрису данного угла.
Решение
Данный угол ВАС изображен
на рисунке. Проведем окружность произвольного радиуса с центром в
вершине А. Она пересечет стороны угла в точках В и С.
Затем проведем две окружности одинакового радиуса ВС с центрами в точках B и С. Они пересекутся в двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС.
Слайд 10
Рассмотрим треугольники АСЕ и АВЕ. Они равны по
трем сторонам. В самом деле, АЕ — общая сторона;
АС и АВ равны как радиусы одной и той же окружности; СЕ = ВЕ по построению.
Из равенства треугольников АСЕ и АВЕ следует, что АСАЕ = АВАЕ, т. е. луч АЕ — биссектриса данного угла ВАС.
Слайд 11
Построение перпендикулярных прямых.
Задача
Даны прямая и точка на ней.
Построить прямую, проходящую через данную точку и перпендикулярную к
данной прямой.
Решение
Данная прямая а и данная точка М, принадлежащая этой прямой, изображены на рисунке .
На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МB. Затем построим две окружности с центрами А и В радиуса АВ. Они пересекаются в двух точках: Р и Q.
Проведем прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая — искомая, т. е. что она перпендикулярна к данной прямой а.
Слайд 12
В самом деле, так как медиана РМ равнобедренного
треугольника РАВ является также высотой, то РМ ┴ а.
Слайд 13
Система автоматизированного проектирования КОМПАС-ГРАФИК
Системы автоматизированного проектирования (САПР) являются
векторными графическими редакторами, предназначенными для создания чертежей.
При классическом черчении
с помощью карандаша, линейки и циркуля производится построение элементов чертежа (отрезков, окружностей, прямоугольников и т.д.) с точностью, которую предоставляют чертежные инструменты. Использование САПР позволяет создавать чертежи с абсолютной точностью и обеспечивает возможность реализации сквозной технологии проектирования и изготовления деталей. На основе компьютерных чертежей генерируются управляющие программы для станков с числовым программным управлением (ЧПУ), в результате по компьютерным чертежам изготавливаются высокоточные детали из металла, дерева и т.д.
Слайд 14
В центре рабочего окна КОМПАС-ГРАФИК размещается система координат.
Положение курсора отсчитывается от начала системы координат, а текущие
значения его координат X и Y отображаются в правой часты Строки текущего состояния, расположенной в нижней части окна приложения.
Создание и редактирование чертежа реализуется с помощью Инструментальной панели, которая по умолчанию размещается в левом верхнем углу окна приложения. Инструментальная панель включает в себя пять различных рабочих панелей, каждая из которых содержит набор кнопок определенного функционального назначения и Панель переключения, которая обеспечивает переход от одной рабочей панели к другой.
Слайд 15
Окно системы автоматизированного проектирования
КОМПАС-ЗD
Слайд 16
Инструментальная панель
Рабочая панель Геометрические построения содержит кнопки, позволяющие
рисовать на чертеже определенные объекты: точка, отрезок, окружность, прямоугольник
и др.
Панель Редактирование содержит кнопки, которые позволяют вносить изменения в чертеж, производя над объектами различные операции: перемещение, копирование, масштабирование и т.д.
Панель Выделение позволяет осуществить различные варианты выделения объектов: отдельные объекты, группы объектов и т.д.
Панель Измерения позволяет измерять расстояния (вычисляются и отображаются в миллиметрах), углы (в градусах), периметры и площади различных объектов.
Панель Размеры и технологические обозначения позволяет грамотно оформить чертеж: обозначить на чертеже размеры деталей, сделать надписи и т.д.
Слайд 18
Построение основных чертежных объектов
Выбор создаваемого чертежного объекта (точка,
отрезок, окружность, прямоугольник и т.д.) осуществляется с помощью панели
Геометрические построения. После выбора объекта щелчком мыши по соответствующей кнопке появляется Строка параметров объекта. Каждый объект обладает определенным набором параметров, которые характеризуют его размеры и положение на чертеже.
Например, после выбора на панели Геометрические построения кнопки Ввод отрезка появится строка с параметрами отрезка: координатами его начальной и конечной точек, длиной , углом наклона и стилем линии.
Слайд 19
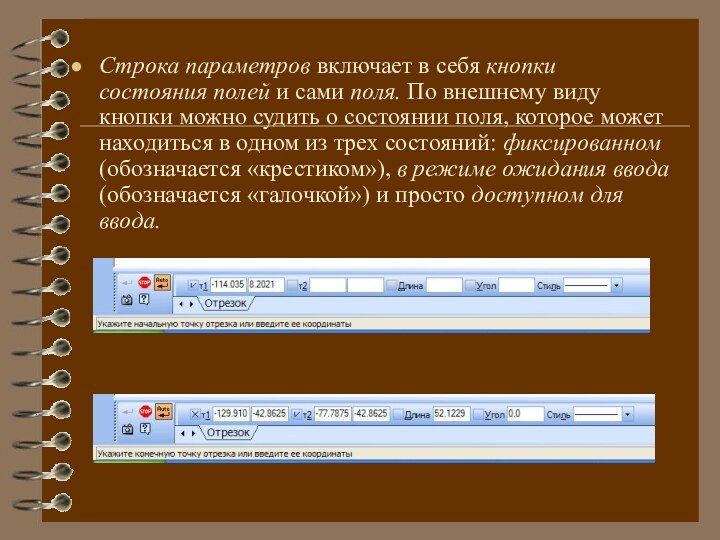
Строка параметров включает в себя кнопки состояния полей
и сами поля. По внешнему виду кнопки можно судить
о состоянии поля, которое может находиться в одном из трех состояний: фиксированном (обозначается «крестиком»), в режиме ожидания ввода (обозначается «галочкой») и просто доступном для ввода.
Слайд 20
При создании и редактировании объектов работа со Строкой
параметров сводится к активизации нужных полей и вводу в
них заданных параметров. После ввода минимального набора параметров, достаточных для построения объекта (для отрезка координат начальной и конечной точек), система автоматически создает объект.
Можно осуществлять Автоматический ввод параметров, Ручной ввод параметров и Ввод параметров с использованием Геометрического калькулятора.
Слайд 21
Построение отрезка в автоматическом режиме
На панели Геометрические построения
щелкнуть по кнопке Ввод отрезка. Появится Строка параметров отрезка,
а в Строке сообщений появится запрос Укажите начальную точку отрезка или введите ее координаты.
Установить курсор в поле чертежа на точку с начальными координатами отрезка и произвести щелчок. При этом в поля координат точки т1 будут внесены значения координат указанной точки на чертеже, а в Строке параметров символ «галочка» сменится на символ «крестик», это означает, что введенные параметры зафиксированы.
Установить курсор в поле чертежа на точку т2 с конечными координатами отрезка и произвести щелчок. Отрезок построен.
Слайд 23
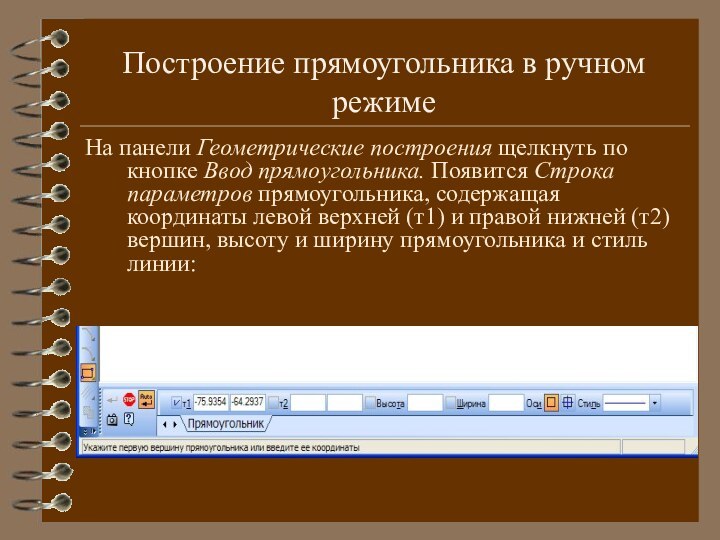
Построение прямоугольника в ручном режиме
На панели Геометрические построения
щелкнуть по кнопке Ввод прямоугольника. Появится Строка параметров прямоугольника,
содержащая координаты левой верхней (т1) и правой нижней (т2) вершин, высоту и ширину прямоугольника и стиль линии:
Слайд 24
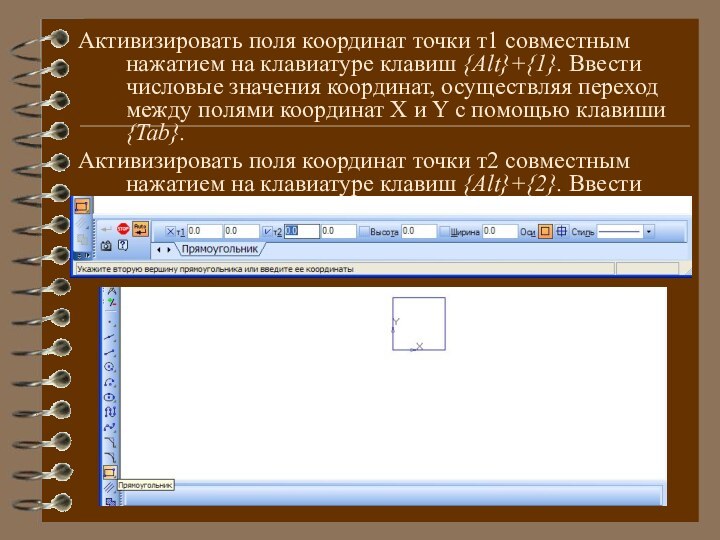
Активизировать поля координат точки т1 совместным
нажатием на клавиатуре
клавиш {Alt}+{1}. Ввести числовые значения координат, осуществляя переход между
полями координат X и Y с помощью клавиши {Tab}.
Активизировать поля координат точки т2 совместным нажатием на клавиатуре клавиш {Alt}+{2}. Ввести числовые значения координат. Прямоугольник построен.
Слайд 25
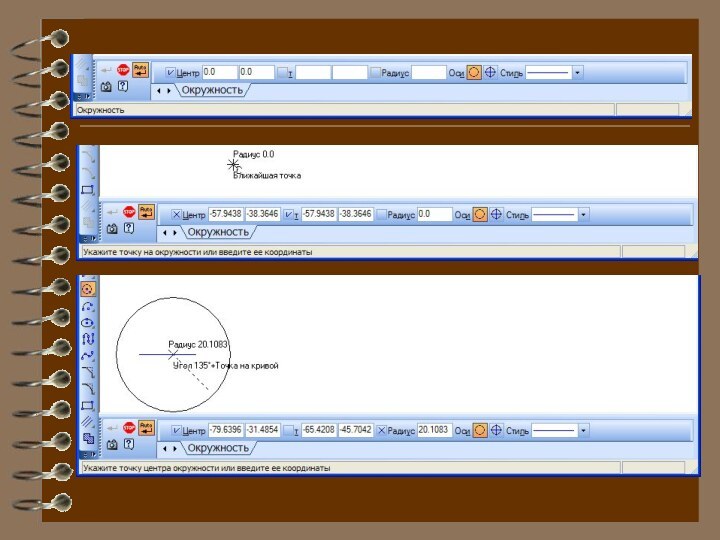
Построение окружности с использованием Геометрического калькулятора.
На панели Геометрические
построения щелкнуть по кнопке Ввод окружности. Появится Строка параметров
окружности, содержащая координаты центра окружности, точки на окружности, радиуса окружности и стиль линии.
Установить курсор в поле чертежа на точку центра окружности и произвести щелчок, в поля координат центра окружности будут внесены значения координат указанной на чертеже точки.
Щелкнуть правой клавишей мыши в поле Радиус окружности и в появившемся меню выбрать пункт Длина кривой. Курсор примет форму мишени.
Выбрать отрезок и щелкнуть левой клавишей мыши. Система автоматически измерит длину выбранного отрезка и построит окружность с таким радиусом.
Слайд 27
Выполнение геометрических построений
Системы автоматизированного проектирования позволяют создавать чертежи
и выполнять геометрические построения. В школьном курсе геометрии рассматриваются
геометрические построения с использованием линейки и циркуля, такие построения можно выполнять и на компьютере.
Рассмотрим задачу о построении перпендикуляра к прямой.
Условия задачи следующие: Даны прямая и точка на ней. Построить прямую через данную точку и перпендикулярную к данной прямой.
Составим сначала алгоритм выполнения заданного построения.
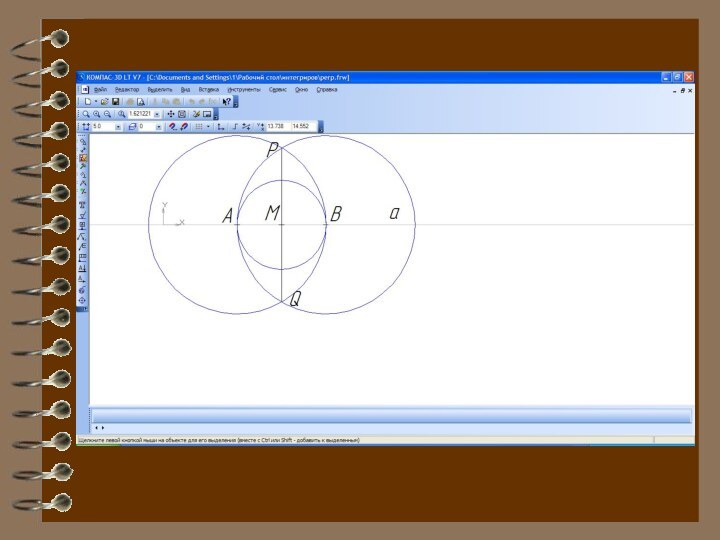
Построить прямую а и точку М на ней.
На равных расстояниях от точки М построить на прямой точки А и В.
Построить две окружности с центрами в точках А и В с радиусом АВ.
Через точки пересечения окружностей Р и Q провести прямую. Данная прямая пройдет через точку М и будет являться перпендикуляром к прямой а.
Слайд 28
Теперь выполним построение в соответствие с разработанным алгоритмом
с использованием системы КОМПАС-ГРАФИК.
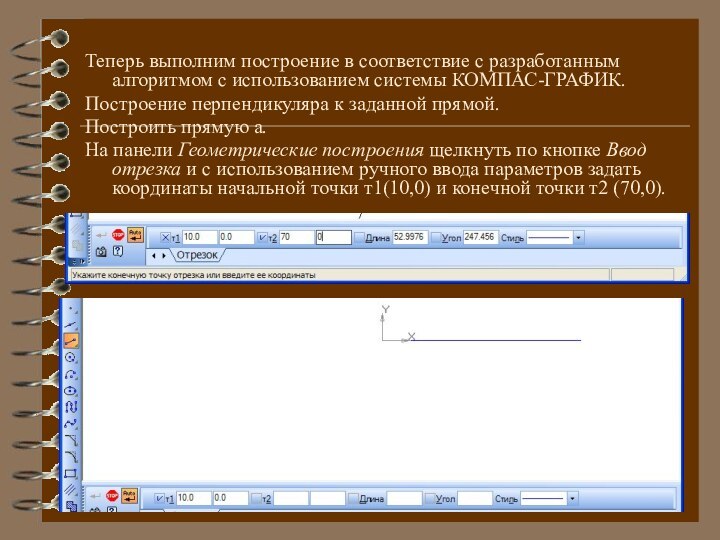
Построение перпендикуляра к заданной прямой.
Построить прямую
а.
На панели Геометрические построения щелкнуть по кнопке Ввод отрезка и с использованием ручного ввода параметров задать координаты начальной точки т1(10,0) и конечной точки т2 (70,0).
Слайд 29
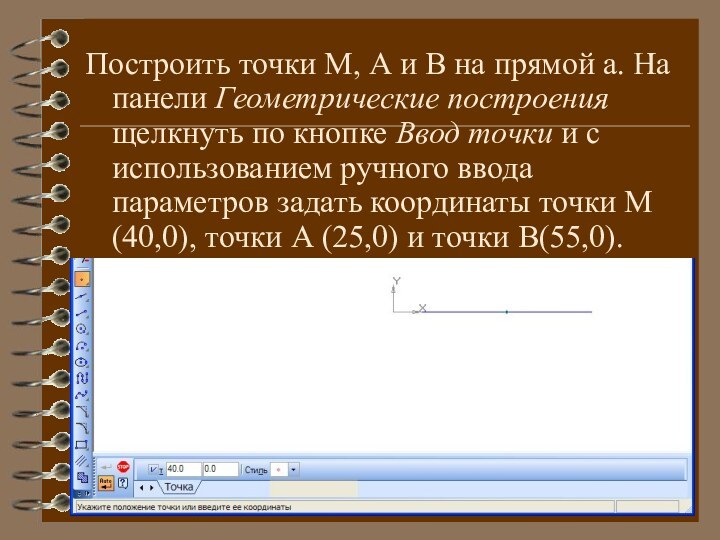
Построить точки М, А и В на прямой
а. На панели Геометрические построения щелкнуть по кнопке Ввод
точки и с использованием ручного ввода параметров задать координаты точки М (40,0), точки А (25,0) и точки В(55,0).
Слайд 31
Построить окружность с центром в точке А и
с радиусом АВ. На панели Геометрические построения щелкнуть по
кнопке Ввод окружности и с использованием ручного
ввода параметров задать координаты центра (25,0).
Задать радиус окружности с использованием Геометрического калькулятора, для этого щелкнуть правой клавишей мыши в поле Радиус окружности и в появившемся меню выбрать пункт Между двумя точками. После того как курсор примет форму мишени, щелкнуть по точкам А и В. Окружность с заданным радиусом будет построена.
Слайд 32
Аналогично построить окружность с центром в точке В
и с радиусом АВ.
Соединить точки пересечения окружностей отрезком. Задать
начальную и конечную точки отрезка с использованием Геометрического калькулятора, выбрав пункт меню Пересечение.
Ввести на чертеже обозначения. Выбрать на Панели управления кнопку Размеры и технологические обозначения, и на появившейся панели щелкнуть по кнопке Ввод текста. Ввести обозначения.
Алгоритм построения перпендикуляра к заданной точке прямой выполнен.
Слайд 34
Практические задания
по группам
Построить угол, равный данному.
Построить биссектрису угла
Слайд 35
Практическое задание. «Построение угла равного заданному».
Отложить угол
равный заданному углу А от луча ОМ.
Составим сначала
алгоритм выполнения заданного построения:
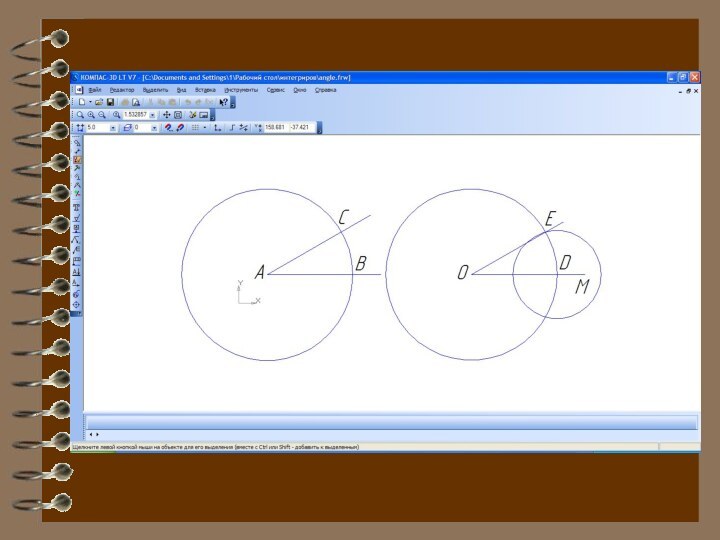
1. Построить окружность произвольного радиуса с центром в вершине заданного угла А, которая пересечет стороны угла в точках В и С.
2. Построить окружность того же радиуса с центром в начале заданного луча ОМ, которая пересечет луч в точке D.
3. Построить окружность с центром в точке D и радиусом BC.
4. Обозначить точку пересечения окружностей с центрами O и D, не лежащую на луче ОМ, буквой E.
5. Полученный угол MOE равен заданному A.
Слайд 36
Построить произвольный угол А (ввести отрезки с использованием
автоматического ввода параметров).
Построить произвольный луч ОМ (ввести отрезок
с использованием автоматического ввода параметров).
Построить окружность с центром в точке А (с использованием ручного ввода) и произвольного радиуса (с использованием автоматического ввода).
Обозначить точки пересечения окружности со сторонами угла буквами B и С.
Слайд 37
Построить окружность с центром в точке О (с
использованием ручного ввода) и заданного радиуса AB (с использованием
геометрического калькулятора).
Для этого щелкнуть по полю радиус правой кнопкой мыши и в контекстном меню выбрать пункт Между 2 точками.
Слайд 38
Отметить на чертеже точки A и B, окружность
заданного радиуса будет построена.
Обозначить точку пересечения окружности с
лучом OM буквой D.
Построить окружность с центром в точке D заданного радиуса BC.
Обозначить точку пересечения окружностей буквой E.
Соединить отрезком точки О и Е, угол EOM равный углу A построен.
Слайд 40
Практическое задание. «Построение биссектрисы угла». Дан неразвернутый угол
А. Построить его биссектрису.
Начертим геометрические объекты, заданные в условии
задачи: два отрезка, исходящих из одной точки под произвольным неразвернутым углом.
Построить два отрезка, исходящие из одной точки (начертить отрезки с использованием автоматического ввода параметров).
Ввести обозначение угла на чертеже буквой А с помощью панели Размеры и технологические обозначения.
Слайд 41
Построим окружность произвольного радиуса с центром в вершине
заданного угла А.
Щелкнуть на кнопке Ввод окружности и построить
окружность произвольного радиуса с центром в точке А (в режиме автоматического ввода).
Активизировать панель Размеры и технологические обозначения, щелкнуть на кнопке Ввод текста и ввести обозначения точек пересечения окружности со сторонами угла буквами В и С.
Слайд 43
Построим две окружности радиуса ВС с центрами» в
точках В и С.
5. Выбрать инструмент Ввод окружности и построить
две окружности заданного радиуса с центрами в точках В и С (с использованием Геометрического калькулятора).
Для этого щелкнуть на поле радиус правой кнопкой мыши и в контекстном меню выбрать пункт Между 2 точками. Точку пересечения окружностей обозначить Е.
Слайд 44
Через вершину угла А и точку пересечения окружностей
Е проведем прямую.
6. Щелкнуть на кнопке Ввод отрезка и начертить
отрезок через точки А и Е (в режиме автоматического ввода).
Луч АЕ будет являться биссектрисой заданного угла.
Слайд 45
Домашнее задание
1 уровень.
Группам поменяться заданиями.
Построить биссектрису угла
Построить угол,
равный данному.
2 уровень.
Построить середину данного отрезка.
3 уровень.
Построение треугольника по
двум сторонам и углу между ними.
Построение треугольника по трем сторонам.
Выполнить построение на компьютере с использованием САПР и в тетрадях по математике с помощью циркуля и линейки.
Записать доказательство-обоснование построения.