называется
вписанной в многоугольник, а многоугольник –
описанным около
этой окружности.Вписанная окружность
А
В
С
D
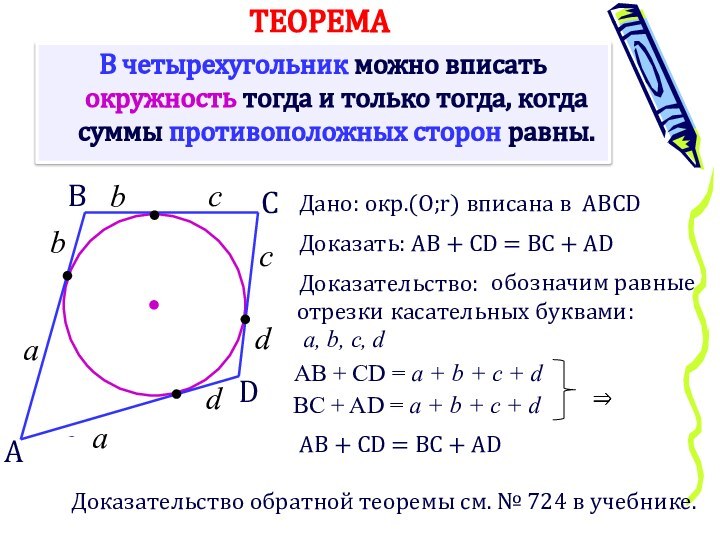
окр.(О;r) вписана в ABCD
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Описанная и вписанная окружность
Содержание
- 2. Если все стороны многоугольника касаются окружности, то
- 3. Не во всякий многоугольник можно вписать окружность.
- 4. В любой треугольник можно вписать окружность и
- 5. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. АПлощадь треугольника
- 6. Не во всякий четырёхугольник можно вписать окружность.
- 7. В четырехугольник можно вписать окружность тогда и
- 8. Формула для радиуса окружности, вписанной в прямоугольный
- 9. Если все вершины многоугольника лежат на окружности,
- 10. Не около всякого многоугольника можно описать окружность.
- 11. Около любого треугольника можно описать окружность и
- 12. Не около всякого четырёхугольника можно описать окружность.
- 13. Скачать презентацию
- 14. Похожие презентации
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.Вписанная окружностьАВСDокр.(О;r) вписана в ABCD
Слайд 2
Если все стороны многоугольника касаются
окружности, то окружность
называется
этой окружности.Слайд 4 В любой треугольник можно вписать окружность и притом
только одну.
А
Доказать: существует окр.(О;r),
вписанная в треугольникДоказательство:
Проведём биссектрисы, которые пересекаются в одной точке – О.
ОК = ОЕ = ОР, где ОК АВ, ОЕ ВС, ОР АС, по свойству биссектрис.
О – центр окружности, ОК, ОЕ, ОР радиусы.
ТЕОРЕМА
В
С
О
К
Е
Р
Центр вписанной окружности - точка пересечения биссектрис.
Слайд 5 Площадь треугольника равна произведению его полупериметра на радиус
вписанной окружности.
А
Площадь треугольника
Слайд 7 В четырехугольник можно вписать окружность тогда и только
тогда, когда суммы противоположных сторон равны.
ТЕОРЕМА
А
В
С
D
Дано: окр.(О;r)
вписана в ABCDДоказательство:
Доказать: AB + CD = BC + AD
a
a
b
b
c
c
d
d
AB + CD = a + b + c + d
BC + AD = a + b + c + d
AB + CD = BC + AD
Доказательство обратной теоремы см. № 724 в учебнике.
обозначим равные
отрезки касательных буквами:
а, b, c, d
Слайд 8
Формула для радиуса окружности,
вписанной в прямоугольный треугольник
Доказательство:
СКОЕ
– квадрат, значит, СК = СЕ = r
По
свойству касательных: ВЕ = ВМ = а - r
АК = АМ = b - r
AB = AM + BM
c = b – r + a - r
2r = a + b - c
АС, ВС, АВ – касательные и
r
r
b - r
а - r
b - r
а - r
Слайд 9
Если все вершины многоугольника лежат
на окружности, то
окружность называется
описанной около многоугольника, а многоугольник – вписанным
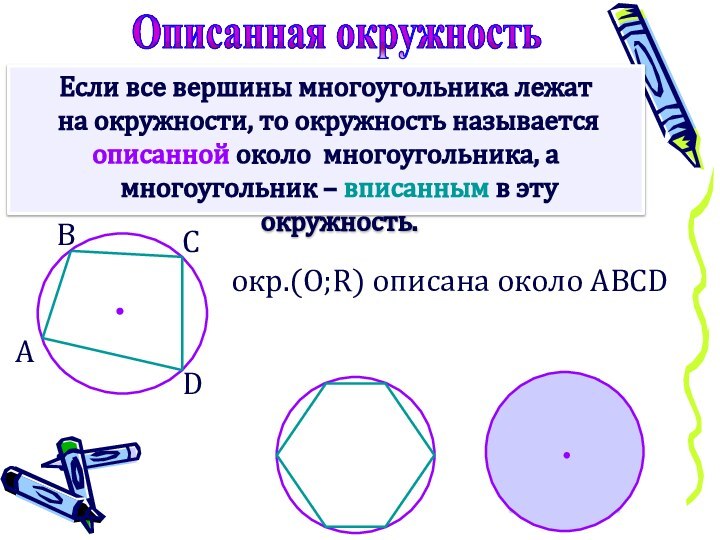
в эту окружность.Описанная окружность
окр.(О;R) oписана около ABCD
А
В
С
D
Слайд 11 Около любого треугольника можно описать окружность и притом
только одну.
Доказать: существует окр.(О;R),
описанная около треугольника
Доказательство:
Проведём серединные перпендикуляры
ОА = ОВ = ОС, по свойству серединных перпендикуляров.
О – центр окружности, ОА, ОВ, ОС – радиусы.
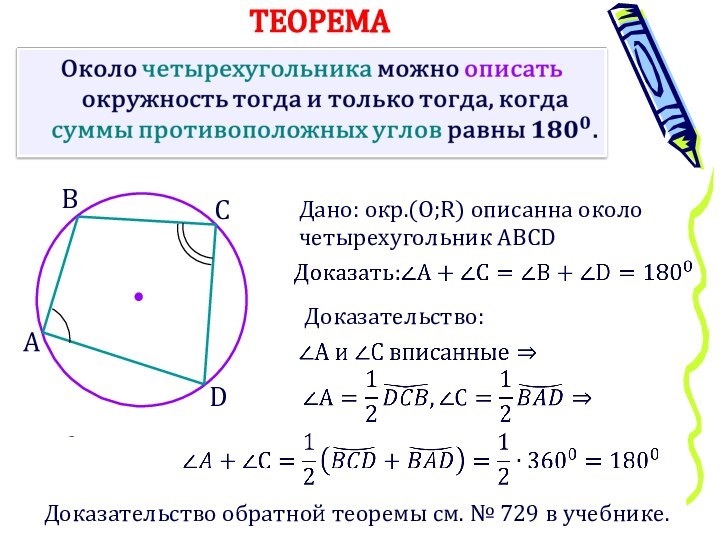
ТЕОРЕМА
А
В
С
О
Центр описанной окружности - точка пересечения серединных перпендикуляров.
