- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Пирамида
Содержание
- 2. пирамида Составила учитель математики МОУ «Гимназия им. Горького А.М.»:Фабер Г.Н.
- 3. Информационно-коммуникативную компетентность учащихся: учить, искать и находить
- 4. содержаниеопределение пирамидывиды пирамидправильные пирамидыпостроение правильной пирамидысвойства правильной пирамидыплощадь поверхностиплощадь поверхности площадь поверхности пирамиды
- 5. Определениепирамида это n-треугольниковэлементы пирамидыSBCDEАвершинаМногогранникn-угольник в основании иоснованиебоковые гранибоковые ребравысота
- 6. Высота проецируетсяВ вершину основанияНа сторону основанияВо внутреннюю область основанияВо внешнюю область основания
- 7. Высота проецируется в центр описанной окружностиСвойстваsABC123645 1. SA=SB=SC 2. ∠1=∠2=∠3 3. ∠4=∠5=∠6
- 8. Высота проецируется в центр вписанной окружностисвойстваSMNK12345 1.SM=SN=SK2.∠1= ∠2= ∠33.∠4= ∠5= ∠6
- 9. Правильная пирамидав основании правильный многоугольниквысота проецируется в центр основанияпостроениесвойстваАПОФЕМА- высота правильной пирамиды
- 10. Построение правильной пирамидывысота пирамидыоснованиецентр основания
- 11. Свойства правильной пирамидыSA=SB=SCБоковые ребра образуют равные углы
- 12. Площадь поверхности пирамидыSпол.=Sбок.+Sосн.
- 13. Пирамиды вокруг нас (Дом. задан. уч-ся)
- 14. Пирамиды вокруг нас«В немой дали застыли пирамиды
- 15. Рабочие группыМатематикиИсторикиИсследователи мировой системы пирамидИсследователи свойств пирамидАрхитекторы
- 16. Математическая точка зренияЕвклид пирамиду определяет как телесную
- 17. Математическая точка зренияАдриен Мари Лежандр в своём
- 18. ЕГИПЕТСКИЕ ПИРАМИДЫИсследование мировой системы пирамидИсследование мировой системы пирамид
- 19. Учебник элементарной геометрии А. Киселева, 1907 г.
- 20. Историческая точка зрения ПИРАМИДА, монументальное сооружение, имеющее
- 21. Историческая точка зренияМексиканская пирамида СолнцаСтупенчатая пирамида в Египте
- 22. АЛЕКСАНДРОВСКИЙ МАЯКИсследование мировой системы пирамид
- 23. Исследование мировой системы пирамидГора Кайлас на Тибете
- 24. Исследование мировой системы пирамид
- 25. Золотое сечениеЗОЛОТОЕ СЕЧЕНИЕ, деление отрезка АС на
- 26. Исследование свойств пирамидПри постройке египетских пирамид было
- 27. Исследование свойств пирамидМы знаем, что отношение между
- 28. Пирамиды в архитектуреТорговый центр в Илинге, Лондон
- 29. Задание группе «Математиков»Изучить пирамиду как геометрическое тело.Найти
- 30. Задание группе «Историков»Найти материалы о первых пирамидах.Изучить
- 31. Задание группе «Исследователей мировой системы пирамид»Установить наличие
- 32. Скачать презентацию
- 33. Похожие презентации
пирамида Составила учитель математики МОУ «Гимназия им. Горького А.М.»:Фабер Г.Н.






























Слайд 3
Информационно-коммуникативную компетентность учащихся:
учить, искать и находить нужные
сведения в огромных информационных массивах, в том числе в
Интернете; развивать способность структурировать и обрабатывать данные в зависимости от конкретной задачи;
учить применять полученные навыки и информацию в организации процесса собственного труда для плодотворной работы в группе и творческом коллективе
Цели урока – формировать
Слайд 4
содержание
определение пирамиды
виды пирамид
правильные пирамиды
построение правильной пирамиды
свойства правильной пирамиды
площадь
поверхностиплощадь поверхности площадь поверхности пирамиды
Слайд 5
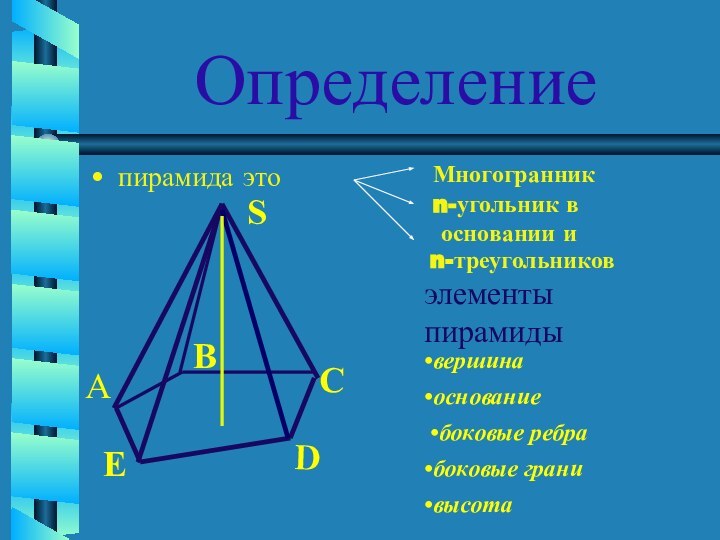
Определение
пирамида это
n-треугольников
элементы пирамиды
S
B
C
D
E
А
вершина
Многогранник
n-угольник в
основании и
основание
боковые
грани
боковые ребра
высота
Слайд 6
Высота проецируется
В вершину основания
На сторону основания
Во внутреннюю область
основания
Во внешнюю область основания
Слайд 7
Высота проецируется в центр описанной окружности
Свойства
s
A
B
C
1
2
3
6
4
5
1. SA=SB=SC
2. ∠1=∠2=∠3
3. ∠4=∠5=∠6
Слайд 8
Высота проецируется в центр вписанной окружности
свойства
S
M
N
K
1
2
3
4
5
1.SM=SN=SK
2.∠1= ∠2=
∠3
3.∠4= ∠5= ∠6
Слайд 9
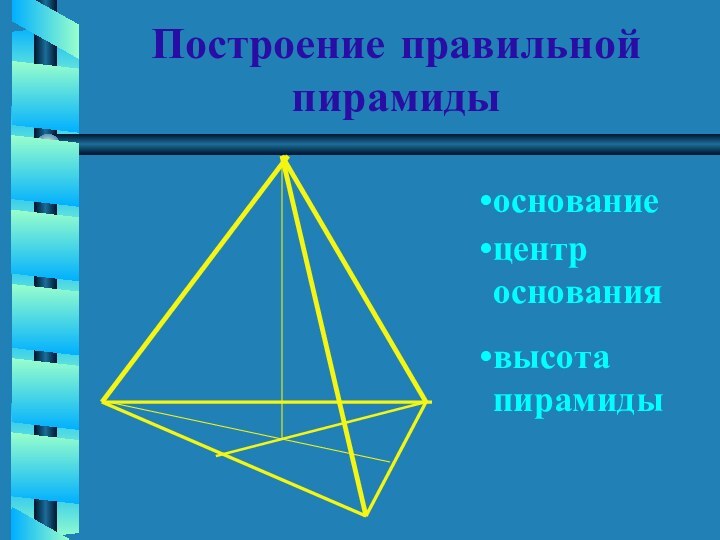
Правильная пирамида
в основании правильный многоугольник
высота проецируется в центр
основания
построение
свойства
АПОФЕМА- высота правильной пирамиды
Слайд 11
Свойства правильной пирамиды
SA=SB=SC
Боковые ребра образуют равные углы с
плоскостью основания
Боковые ребра образуют равные углы с высотой
SM=SN=SK
Боковые грани
образуют равные углы с основаниемВысота пирамиды образует равные углы с высотами боковых граней
Слайд 14
Пирамиды вокруг нас
«В немой дали застыли пирамиды
фараонов, саркофаги
древней были.
Величавые как вечность, молчаливые как смерть»
Михай Эминеску
Слайд 15
Рабочие группы
Математики
Историки
Исследователи мировой системы пирамид
Исследователи свойств пирамид
Архитекторы
Слайд 16
Математическая точка зрения
Евклид пирамиду определяет как телесную фигуру,
ограниченную плоскостями, которые от одной плоскости сходятся к одной
точке.Герон предложил следующее определение пирамиды: «Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник».
Слайд 17
Математическая точка зрения
Адриен Мари Лежандр в своём труде
«Элементы геометрии» в 1794 г. даёт определение: «Пирамида –
телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания».В учебнике XIX в. Фигурировало определение: «пирамида – телесный угол, пересечённый плоскостью».
Слайд 18
ЕГИПЕТСКИЕ ПИРАМИДЫ
Исследование
мировой системы пирамид
Исследование
мировой системы пирамид
Слайд 20
Историческая точка зрения
ПИРАМИДА, монументальное сооружение, имеющее геометрическую
форму пирамиды (иногда ступенчатую или башнеобразную). Пирамидами называют гробницы
древне-египетских фараонов 3 – 2-го тыс. до н. э., а также постаменты храмов в Центральной и Южной Америке, связанные с космологическими культами.Терра-Лексикон: Иллюстрированный
энциклопедический словарь, 1998
Слайд 25
Золотое сечение
ЗОЛОТОЕ СЕЧЕНИЕ, деление отрезка АС на две
части таким образом, что большая его часть АВ относится
к меньшей ВС так, как весь отрезок АС относится к АВ. Приближённо это отношение равно 5/3, точнее 8/5, 13/8 и т. д. Принципы З. с. используются в архитектуре. Термин «З. с.» ввёл Леонардо да Винчи (кон. 15 в.).
Слайд 26
Исследование свойств пирамид
При постройке египетских пирамид было установлено,
что квадрат, построенный на высоте пирамиды, в точности равен
площади каждого из боковых треугольников. Это подтверждается новейшими измерениями.Если сторону основания пирамиды разделить на точную длину года – 365,2422 суток, то получается 10-миллионная доля земной полуоси с большой точностью.
Слайд 27
Исследование свойств пирамид
Мы знаем, что отношение между длиной
окружности и её диаметром есть постоянная величина, хорошо известная
современным математикам, школьникам – это число π = 3,1416… Но если сложить четыре стороны основания пирамиды Хеопса, мы получим 931,22 м. Разделив это число на удвоенную высоту пирамиды (2*148,208), мы получим 3,1416…, то есть число π.
Слайд 29
Задание группе «Математиков»
Изучить пирамиду как геометрическое тело.
Найти определения
пирамиды, которые были сформулированы древними учёными.
Сравнить современные трактовки с
древними.
Слайд 30
Задание группе «Историков»
Найти материалы о первых пирамидах.
Изучить древние
пирамиды с математической точки зрения.
Сформулировать вывод о значимости пирамид
с исторической и математической точек зрения.
Слайд 31
Задание группе «Исследователей мировой системы пирамид»
Установить наличие мест
расположения пирамид на Земле.
Установить связи между местами расположения пирамид.
Сформулировать
вывод о расположении пирамид на Земле.





























