- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
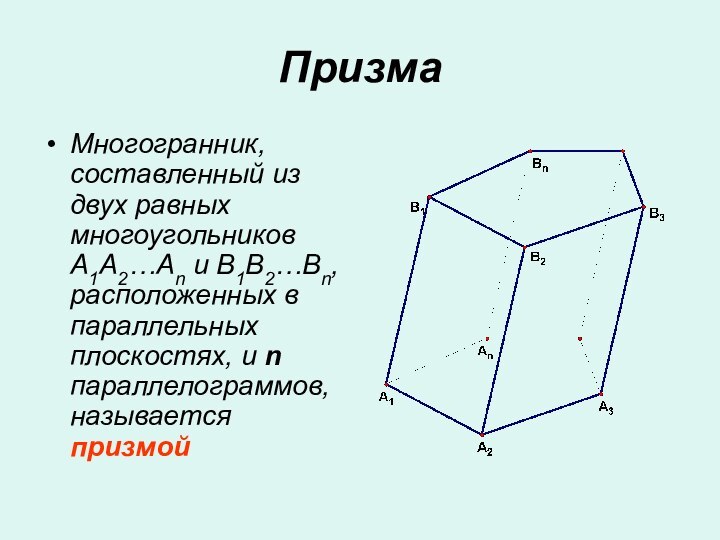
Презентация на тему Призма и ее свойства
Содержание
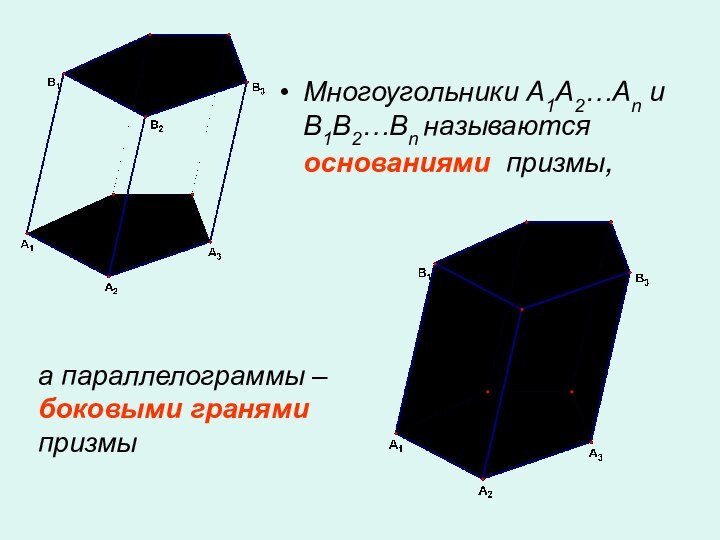
- 2. Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,а параллелограммы – боковыми гранями призмы
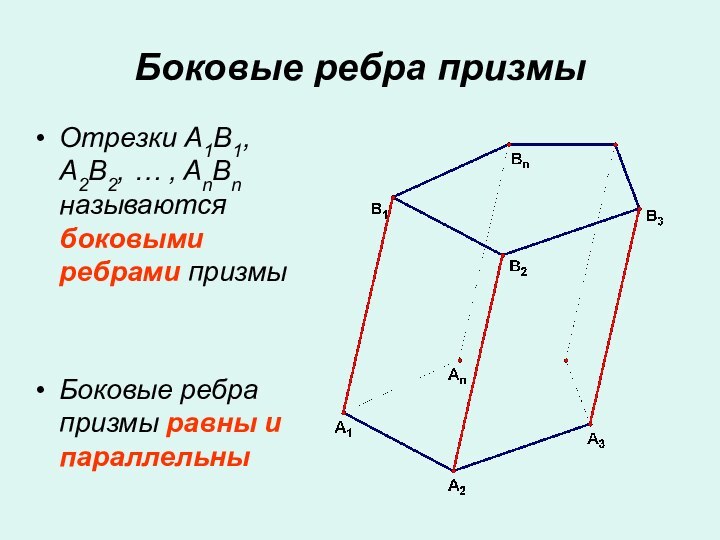
- 3. Отрезки A1B1, A2B2, … , AnBn называются
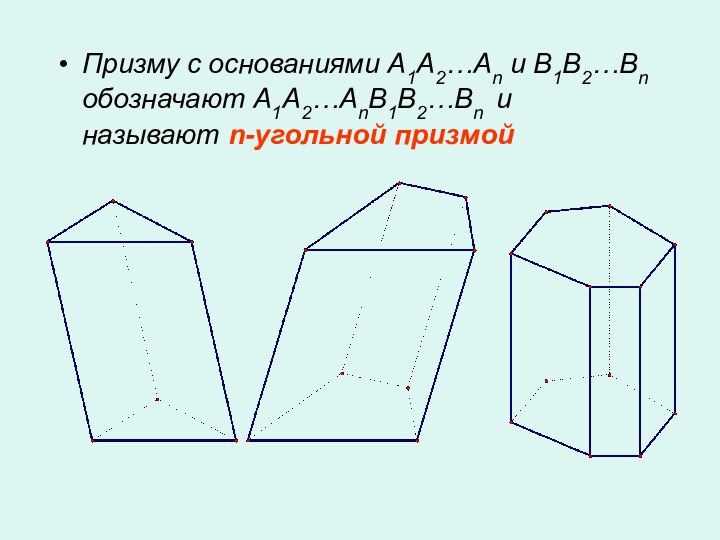
- 4. Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют n-угольной призмой
- 5. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы Высота призмы
- 6. Если боковые ребра призмы перпендикулярны к основаниям,
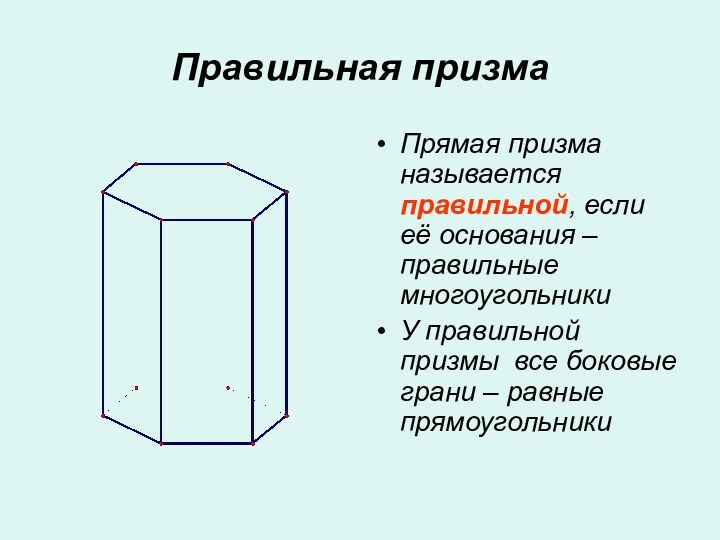
- 7. Правильная призмаПрямая призма называется правильной, если её
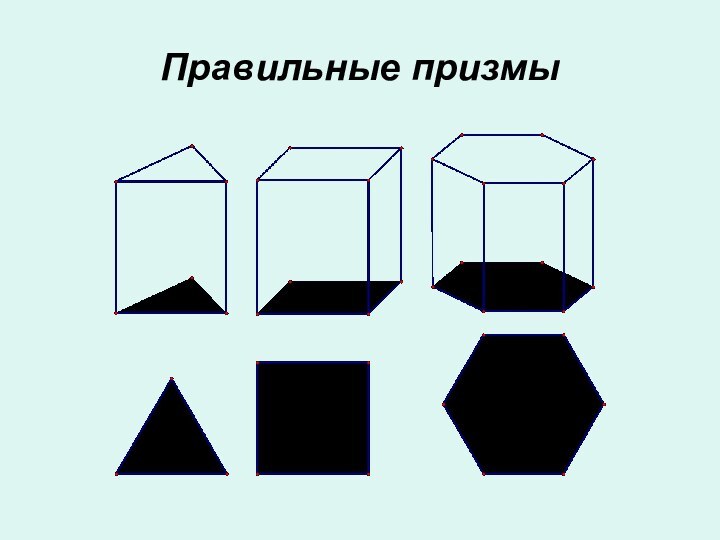
- 8. Правильные призмы
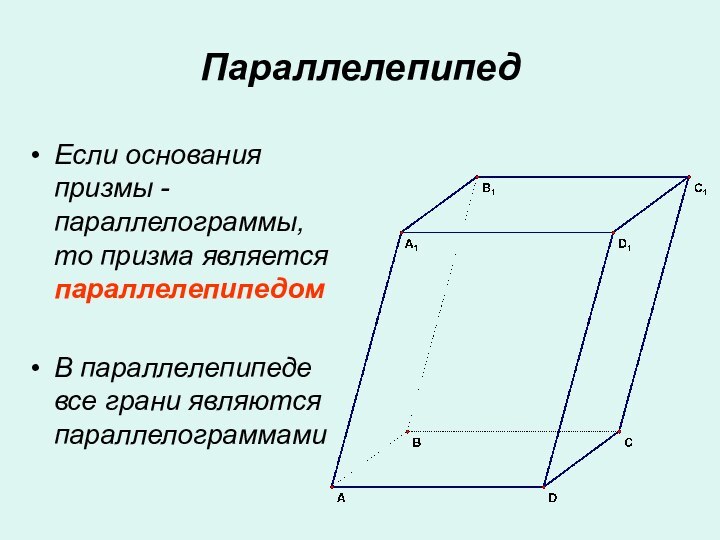
- 9. ПараллелепипедЕсли основания призмы - параллелограммы, то призма является параллелепипедомВ параллелепипеде все грани являются параллелограммами
- 10. Диагонали призмыДиагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
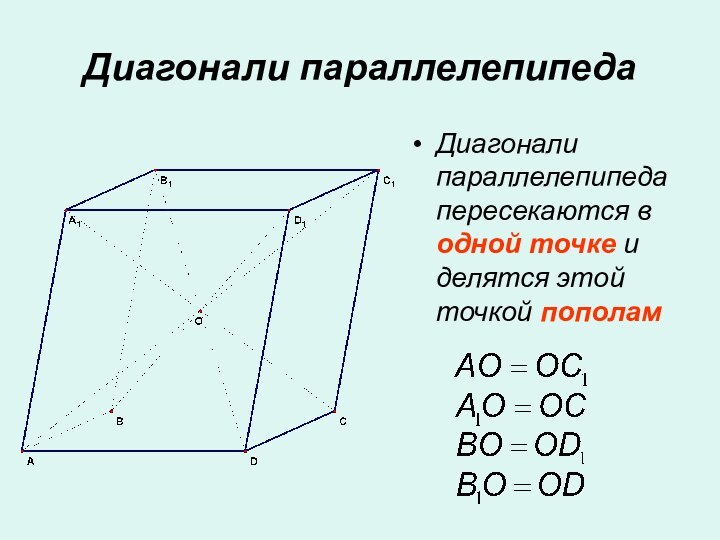
- 11. Диагонали параллелепипедаДиагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
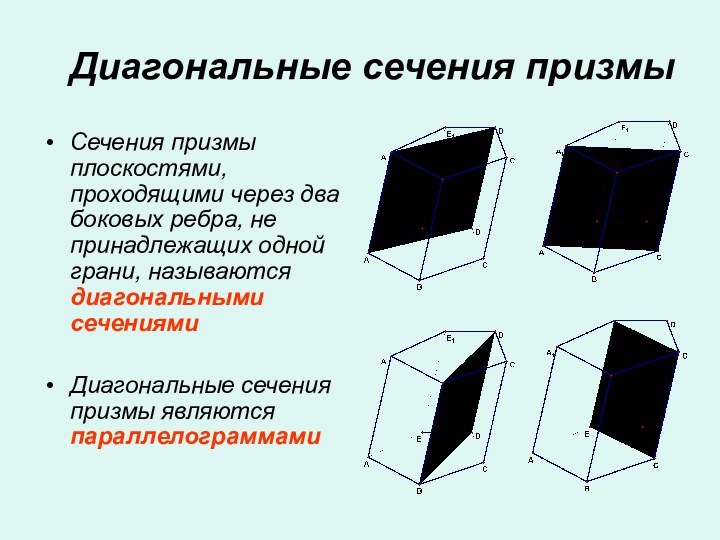
- 12. Диагональные сечения призмыСечения призмы плоскостями, проходящими через
- 13. Диагональные сечения параллелепипеда
- 14. Площадь поверхности призмыПлощадью полной поверхности призмы называется
- 15. Теорема о площади боковой поверхности прямой призмы Теорема.
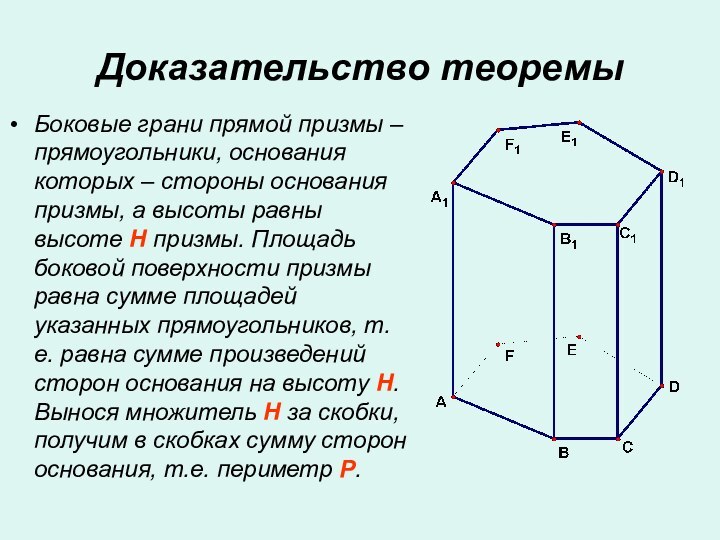
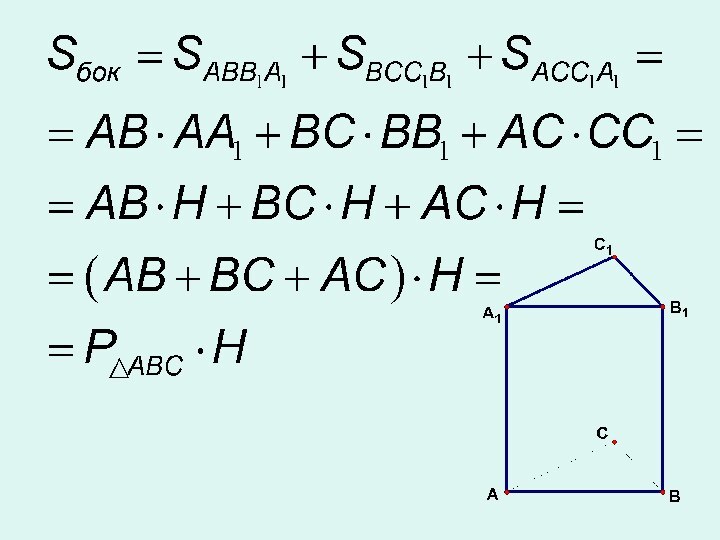
- 16. Доказательство теоремыБоковые грани прямой призмы – прямоугольники,
- 17. Скачать презентацию
- 18. Похожие презентации
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,а параллелограммы – боковыми гранями призмы





Слайд 2
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,
а параллелограммы
– боковыми гранями призмы
Слайд 3 Отрезки A1B1, A2B2, … , AnBn называются боковыми
ребрами призмы
Боковые ребра призмы равны и параллельны
Боковые ребра призмы
Слайд 4 Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn
и называют n-угольной призмой
Слайд 5 Перпендикуляр, проведенный из какой-нибудь точки одного основания к
плоскости другого основания, называется высотой призмы
Высота призмы
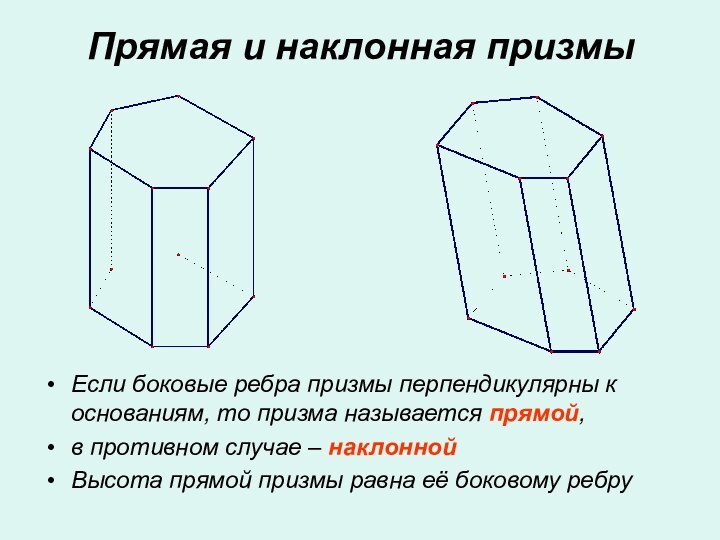
Слайд 6 Если боковые ребра призмы перпендикулярны к основаниям, то
призма называется прямой,
в противном случае – наклонной
Высота прямой
призмы равна её боковому ребруПрямая и наклонная призмы





























