Презентация на тему Построение сечений

школы Пестречинского муниципального района Республики Татарстан
Галяутдинов Ильдар Искандарович.

Руководитель

: учитель информатики Надеждинской основной общеобразовательной школы
Ганеева Гузаль Гилязиевна.

задачи
Задача на построение сечения в тетраэдре
Задачи на построение

сечений в призме

Алгоритм построения сечений в пирамиде и призме

Литература

в школьных учебниках геометрии. Решение этого вида задач способствует

усвоению аксиом стереометрии, следствий из них, систематизации знаний и умений, развитию пространственных представлений и конструктивных навыков.
Сечение выпуклого многогранника есть выпуклый многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с рёбрами многогранника, а стороны – линиями пересечения секущей плоскости с гранями.

две общие точки этих плоскостей и провести через них

прямую. Это основано на аксиомах стереометрии:

1) если две точки прямое лежат в плоскости, то все точки прямой лежат в плоскости

2) если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную прямую.

Решим несколько задач.

Построить точку пересечения прямой MN с плоскостью ABC.



A
C
B
D
M
N

X





решение

AD, точка N лежит на грани BCD. Построить пересечение

прямой MN с плоскостью ABC.

A

C

B

D

M

N

Е

X

решение

Построить сечение тетраэдра плоскостью MNP.

А
С
В
D
N
M
P
Е
Q








решение

точки P,Q и R где R є (AA1C1C), P є

B1C1, Q є AB.

B

C

A

B1

C1

A1

Q

R

P

P1

R1

X

K

E

Y

F

решение

плоскостью, проходящей через точки К, М, N ,

если
К є пл.(CDD1C1), N є пл. (FEE1F1), M є пл.(ABB1A1).

A

B

C

D

E

F

A1

B1

C1

D1

E1

F1

N

K

M

M1

K1

N1

X1

X2

X3

Q

R

X4

P

O

T

L

S

решение

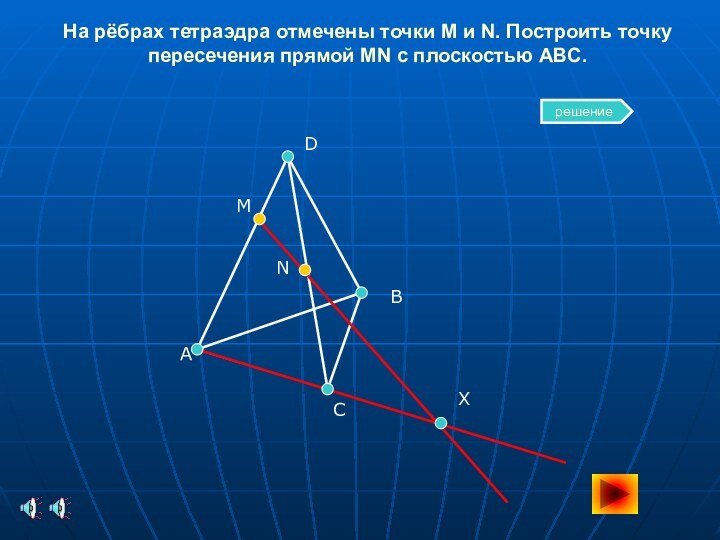
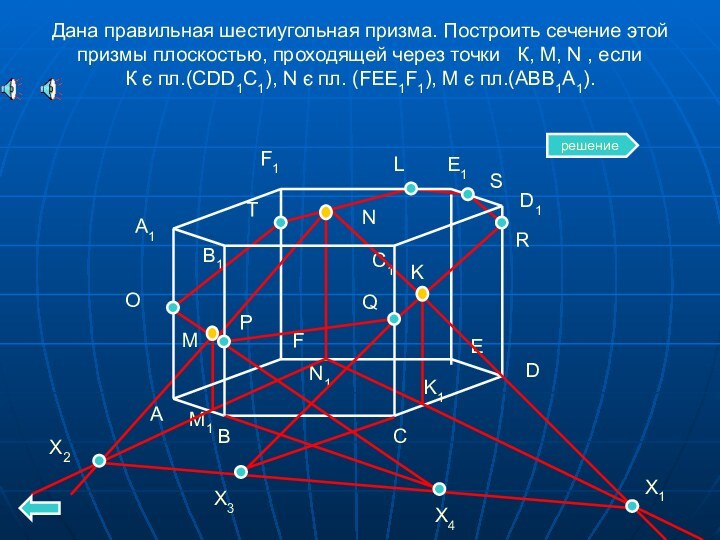
пирамид по трем точкам( пусть точки М, N, K):

Шаг

1. Строим проекции M 1 ,N1, K1 данных точек M, N, K на плоскость основания (параллельно боковым ребрам в случае призм и из вершины пирамиды как из центра проекции в случае пирамид); эту плоскость называют основной.

Шаг 2. Пересекая прямые, соединяющие данные точки с их проекциями, находим точки пересечения этих прямых с основной плоскостью. Проходящая через них прямая есть след сечения на основании. Чтобы ее провести, достаточно найти хотя бы две ее точки.

Шаг 3. Находим точки пересечения следа со сторонами основания или их продолжениями. Используя эти точки и те из данных точек, которые лежат на боковой поверхности многогранника, последовательно находим вершины сечения на боковых ребрах, а в случае призмы – и на сторонах второго основания.

«Математика»
Р.А. Гильманов, С.Ф. Гагуцкий «Как решать конкурсные задачи

по геометрии»
Геометрия 10-11 (учебник). Авторы: Л.С. Атанасян и др.