- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Повторение геометрии
Содержание
- 2. Устная работаД/зРешение задачПроверка д/зЗадача 1Задача 2Задача 3Дано: CBD=35; BF=2см; AD=3см; AF=FC; CAD=ACB.Найти: ADF; FD; BC.РешениеACDFB3212
- 3. Устная работаД/зРешение задачПроверка д/зACDFB32Решение1). Так как CAD=ACB
- 4. Д/зРешение задачУстная работаПроверка д/зЗадача 2Задача 1 Задача 3ADFBДано: AB=BC; CF=FD.Доказать, что AB||DF.ДоказательствоC12
- 5. Д/зРешение задачУстная работаПроверка д/зЗадача 2Задача 1 Задача
- 6. Д/зРешение задачУстная работаПроверка д/зЗадача 2Задача 3Задача 1
- 7. Д/зРешение задачУстная работаПроверка д/зЗадача 2Задача 3Задача 1
- 8. Д/зРешение задачПроверка д/зУстная работаПроверка д/зЗадача 1Задача 2 Из
- 9. Д/зРешение задачПроверка д/зУстная работаПроверка д/зЗадача 1Задача 2Слайд
- 10. Д/зРешение задачПроверка д/зУстная работаПроверка д/зЗадача 2 В параллелограмме
- 11. Д/зРешение задачПроверка д/зУстная работаПроверка д/зЗадача 2РешениеТочка О
- 12. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2 Две
- 13. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2РешениеACBabИскомую
- 14. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2РешениеACBabИскомую
- 15. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2РешениеACBabИскомую
- 16. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2РешениеACBabИскомую
- 17. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2РешениеACBabИскомую
- 18. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2ДоказательствоACBПусть
- 19. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2ACBabИз
- 20. Д/зПроверка д/зРешение задачУстная работаПроверка д/з Точка N лежит
- 21. Д/зПроверка д/зРешение задачУстная работаПроверка д/зОколо всякого треугольника
- 22. Д/зПроверка д/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2BACNПрименяя
- 23. Проверка д/зД/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2 Трапеция
- 24. Проверка д/зД/зРешение задачУстная работаПроверка д/зЗадача 1Задача 2MADBCN
- 25. Проверка д/зД/зРешение задачУстная работаПроверка д/зЗадача 2Задача 2Задача
- 26. Проверка д/зД/зРешение задачУстная работаПроверка д/зЗадача 2Задача 2Задача
- 27. Скачать презентацию
- 28. Похожие презентации

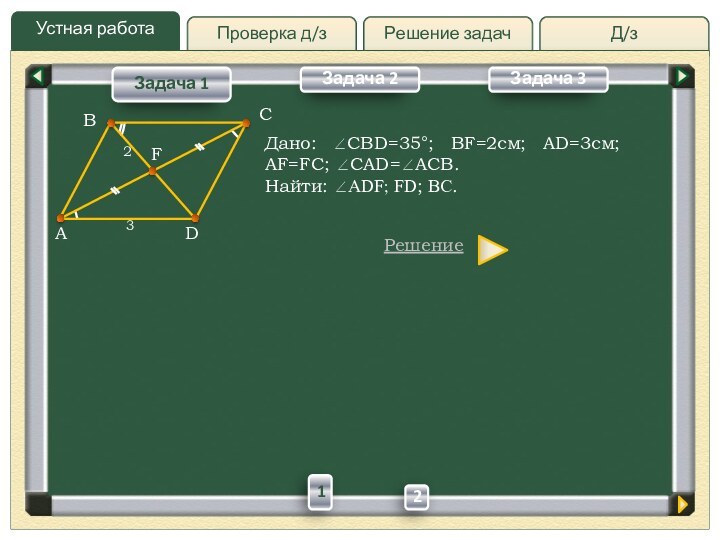





Слайд 2
Устная работа
Д/з
Решение задач
Проверка д/з
Задача 1
Задача 2
Задача 3
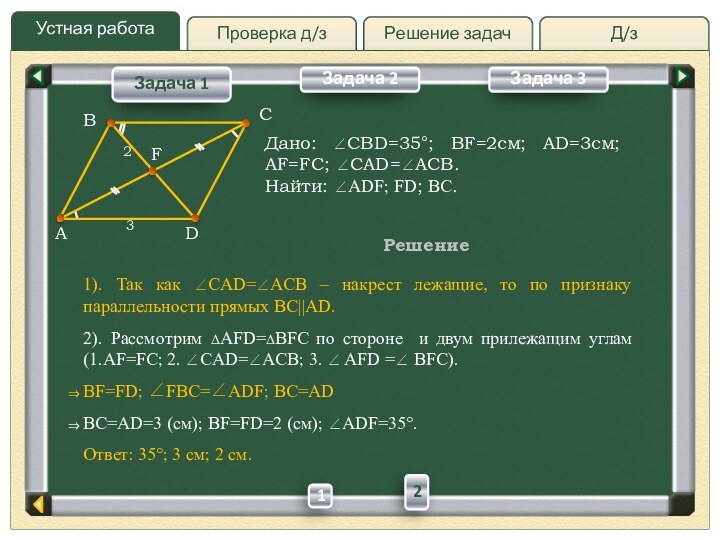
Дано: CBD=35;
BF=2см; AD=3см; AF=FC; CAD=ACB.
Слайд 3
Устная работа
Д/з
Решение задач
Проверка д/з
A
C
D
F
B
3
2
Решение
1). Так как CAD=ACB –
накрест лежащие, то по признаку параллельности прямых BC||AD.
Дано: CBD=35;
BF=2см; AD=3см; AF=FC; CAD=ACB.Найти: ADF; FD; BC.
2). Рассмотрим AFD=BFC по стороне и двум прилежащим углам (1.AF=FC; 2. CAD=ACB; 3. AFD = BFC).
ВF=FD; FBC=ADF; BC=AD
BC=AD=3 (см); ВF=FD=2 (см); ADF=35.
Ответ: 35; 3 см; 2 см.
2
Задача 1
Задача 2
Задача 3
1
Слайд 4
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 2
Задача 1
Задача 3
A
D
F
B
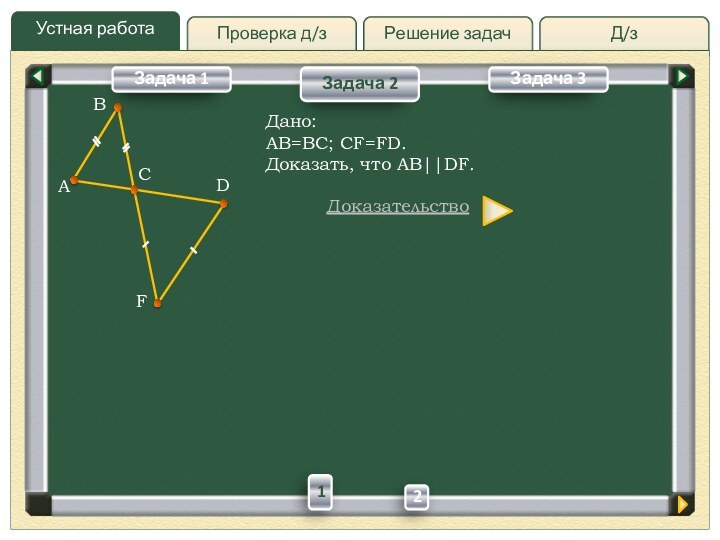
Дано:
AB=BC; CF=FD.
Доказать, что AB||DF.
Доказательство
C
1
2
Слайд 5
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 2
Задача 1
Задача 3
A
D
F
B
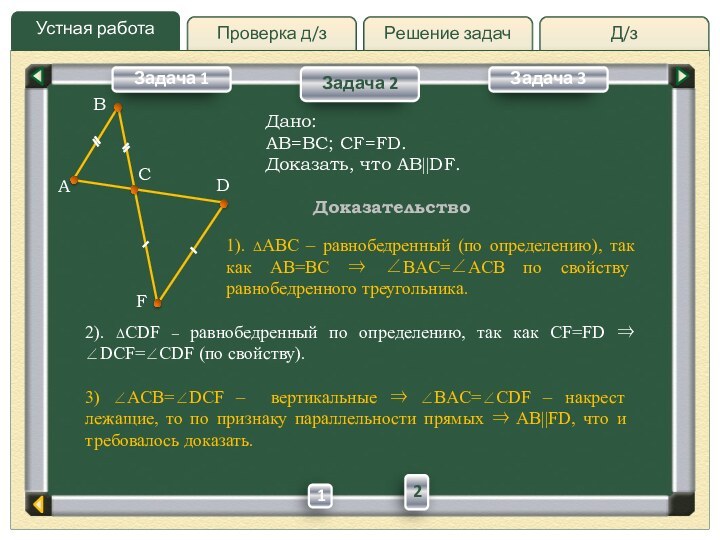
Дано:
AB=BC; CF=FD.
Доказать, что AB||DF.
C
Доказательство
1). ABC – равнобедренный (по определению),
так как AB=BC BAC=ACB по свойству равнобедренного треугольника.2). CDF – равнобедренный по определению, так как CF=FD DCF=CDF (по свойству).
3) ACB=DCF – вертикальные BAC=CDF – накрест лежащие, то по признаку параллельности прямых AB||FD, что и требовалось доказать.
2
1
Слайд 6
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 2
Задача 3
Задача 1
B
A
C
O
D
F
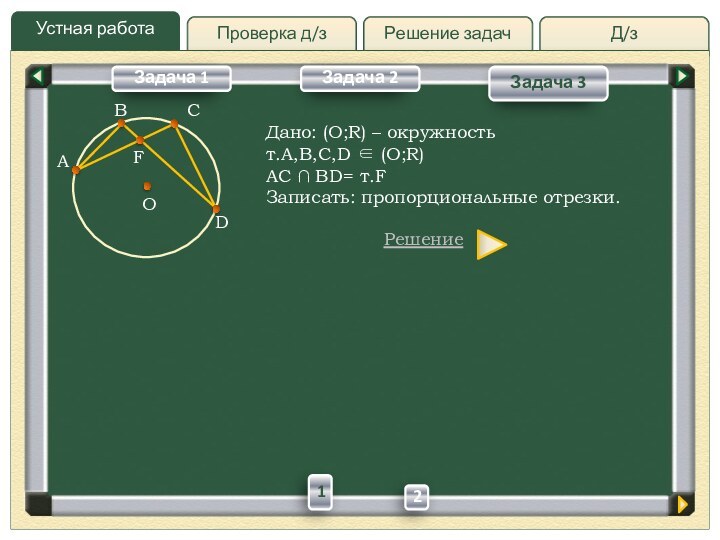
Дано:
(O;R) – окружность
т.A,B,C,D (O;R)
AC ∩ BD= т.F
Записать:
пропорциональные отрезки.Решение
1
2
Слайд 7
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 2
Задача 3
Задача 1
B
A
C
O
D
F
Дано:
(O;R) – окружность
т.A,B,C,D (O;R)
AC ∩ BD= т.F
Записать:
пропорциональные отрезки.Решение
1). ABD=ACD – вписанные, опирающиеся на одну и туже дугу AD.
2). BAC=CDB – вписанные, опирающиеся на одну и туже дугу BC.
3). AFB=CFD – вертикальные стороны AF и DF; BF и CF; AB и CD – сходственные стороны ABF CDF
2
1
Слайд 8
Д/з
Решение задач
Проверка д/з
Устная работа
Проверка д/з
Задача 1
Задача 2
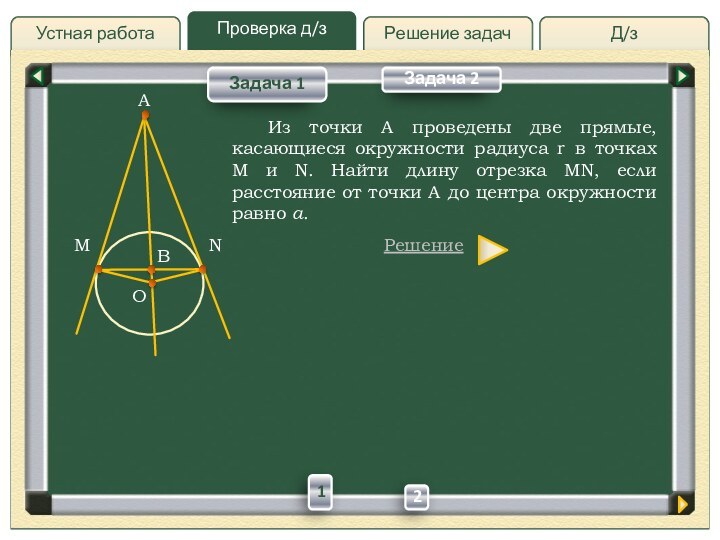
Из точки
А проведены две прямые, касающиеся окружности радиуса r в
точках M и N. Найти длину отрезка MN, если расстояние от точки A до центра окружности равно a.Решение
A
M
N
O
B
1
2
Слайд 9
Д/з
Решение задач
Проверка д/з
Устная работа
Проверка д/з
Задача 1
Задача 2
Слайд 5
Решение
A
M
N
O
B
Задача
1
Задача 2
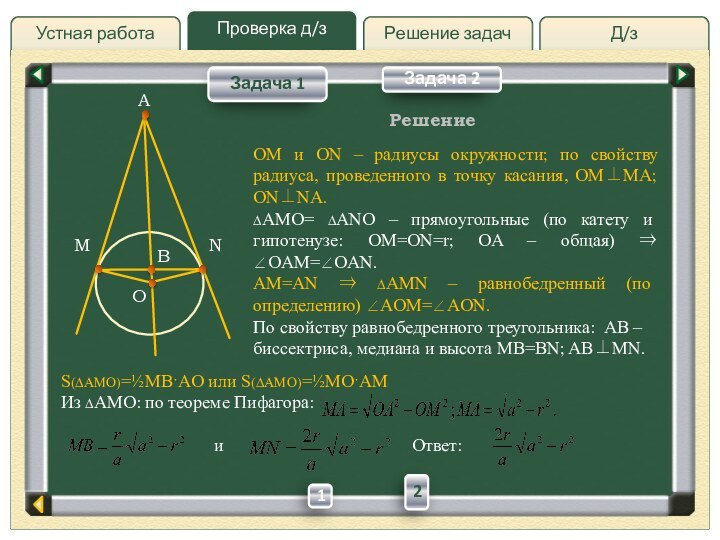
OM и ON – радиусы окружности; по свойству
радиуса, проведенного в точку касания, OMMA; ONNA.∆AMO= ∆ANO – прямоугольные (по катету и гипотенузе: OM=ON=r; OA – общая) OAM=OAN.
AM=AN ∆AMN – равнобедренный (по определению) AOM=AON.
По свойству равнобедренного треугольника: AB – биссектриса, медиана и высота MB=BN; ABMN.
S(∆AMO)=½MBˑAO или S(∆AMO)=½MOˑAM
Из ∆AMO: по теореме Пифагора:
и Ответ:
2
1
Слайд 10
Д/з
Решение задач
Проверка д/з
Устная работа
Проверка д/з
Задача 2
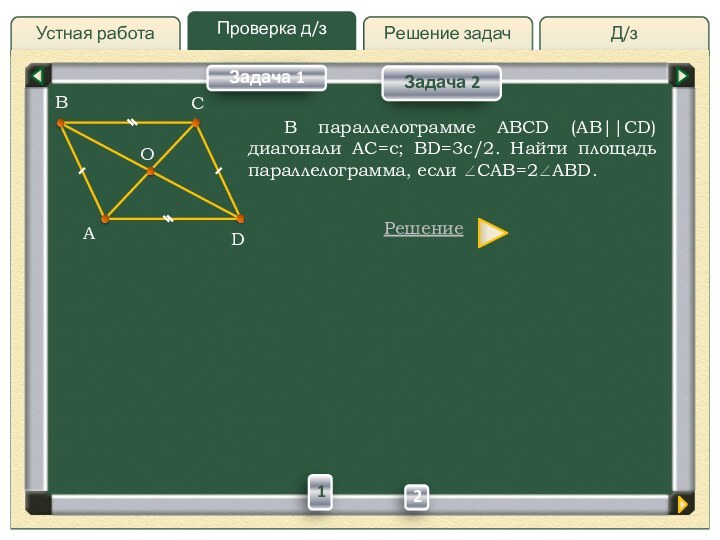
В параллелограмме ABCD
(AB||CD) диагонали AC=c; BD=3с/2. Найти площадь параллелограмма, если CAB=2ABD.
Решение
A
C
D
O
B
Задача
11
2
Слайд 11
Д/з
Решение задач
Проверка д/з
Устная работа
Проверка д/з
Задача 2
Решение
Точка О –
точка пересечения диагоналей параллелограмма ABCD. Для вычисления площади применим
формулу S(ABCD)=½ACˑBDˑsin AOB;S(ABCD)=¾c2ˑsin AOB
Пусть DBA=, тогда CAB=2, AOB=π – 3.
По теореме синусов из ∆AOB:
Тогда, используя формулу sin3, получаем
sin AOB=sin3 =3sin –4sin3=
Ответ:
Задача 2
Задача 1
A
C
D
O
B
3
2
1
Слайд 12
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
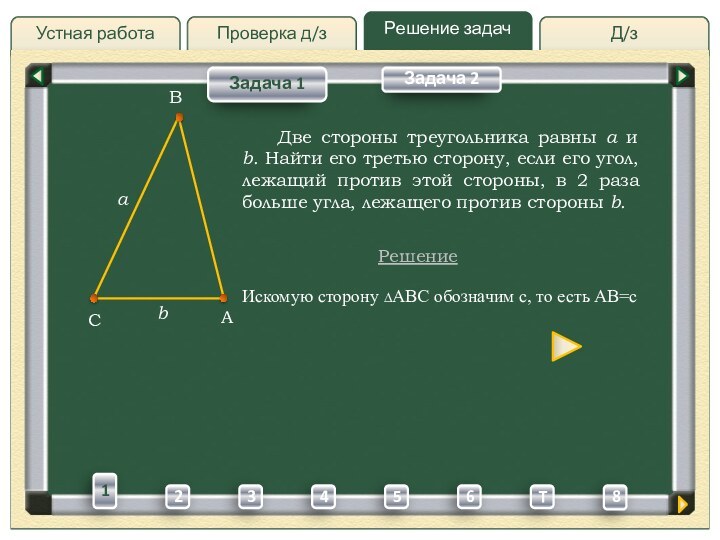
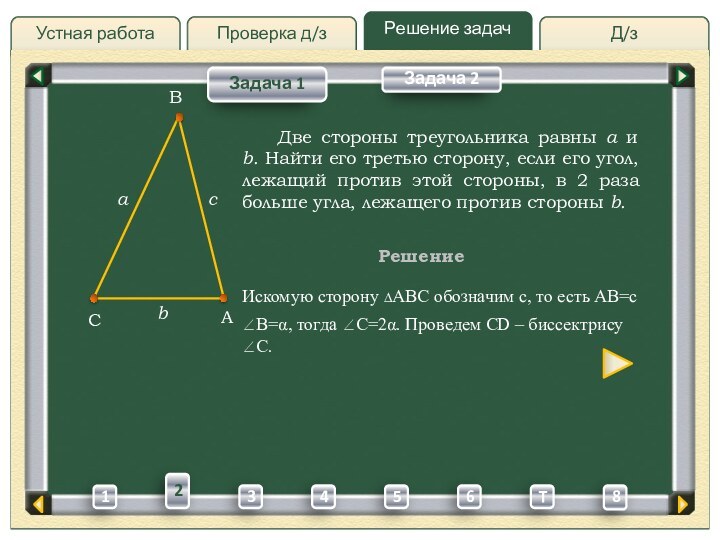
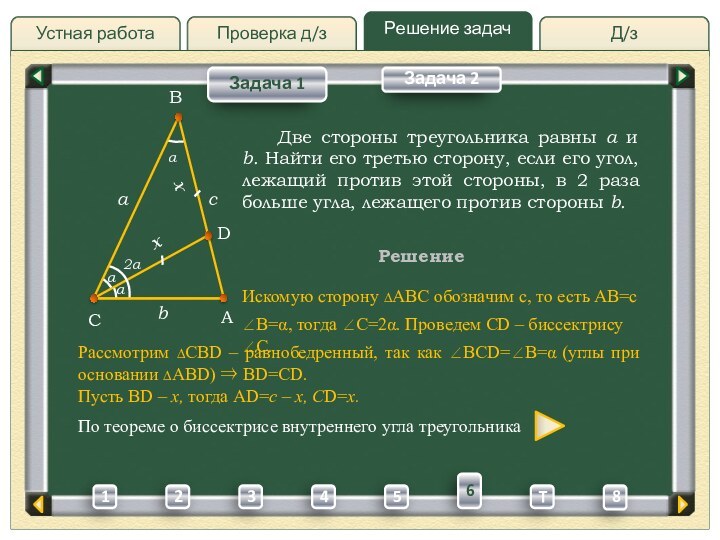
Две стороны
треугольника равны a и b. Найти его третью сторону,
если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b.Решение
A
C
B
a
b
Искомую сторону ∆ABC обозначим c, то есть AB=c
3
4
5
2
6
8
T
1
Слайд 13
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
Решение
A
C
B
a
b
Искомую сторону
∆ABC обозначим c, то есть AB=c
c
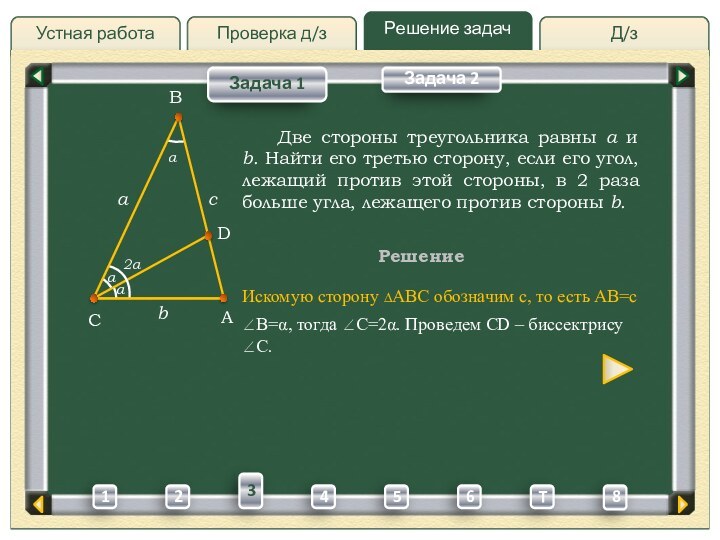
B=, тогда C=2.
Проведем CD – биссектрису C. Две стороны треугольника равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b.
3
4
5
6
1
8
T
2
Слайд 14
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
Решение
A
C
B
a
b
Искомую сторону
∆ABC обозначим c, то есть AB=c
Две стороны треугольника
равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b.c
B=, тогда C=2. Проведем CD – биссектрису C.
2
D
4
5
2
6
1
8
T
3
Слайд 15
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
Решение
A
C
B
a
b
Искомую сторону
∆ABC обозначим c, то есть AB=c
Две стороны треугольника
равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b.c
B=, тогда C=2. Проведем CD – биссектрису C.
2
D
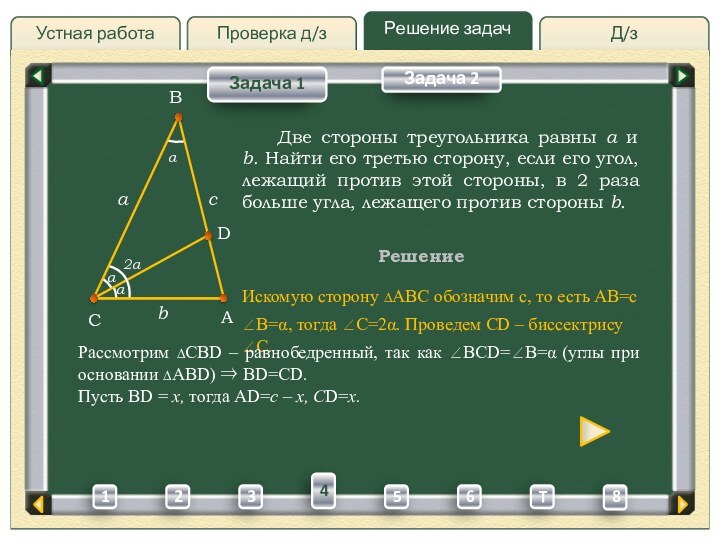
Рассмотрим ∆CBD – равнобедренный, так как BCD=B= (углы при основании ∆ABD) BD=CD.
Пусть BD = x, тогда AD=c – x, CD=x.
3
5
2
6
1
8
T
4
Слайд 16
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
Решение
A
C
B
a
b
Искомую сторону
∆ABC обозначим c, то есть AB=c
Две стороны треугольника
равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b.c
B=, тогда C=2. Проведем CD – биссектрису C.
2
D
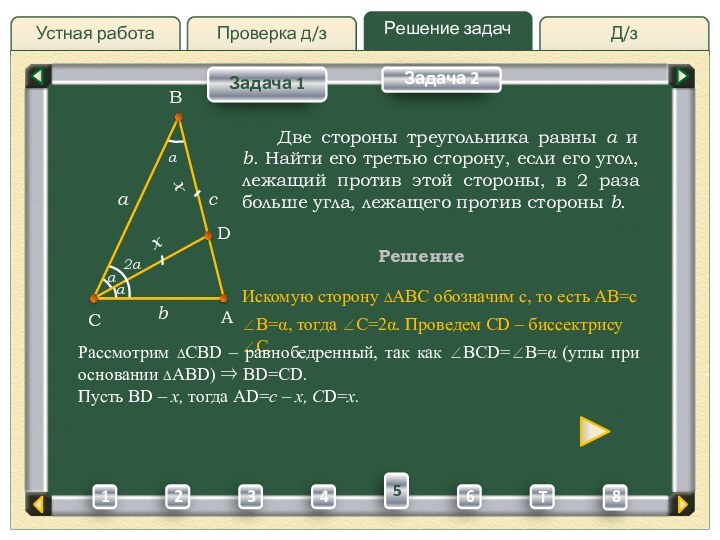
Рассмотрим ∆CBD – равнобедренный, так как BCD=B= (углы при основании ∆ABD) BD=CD.
Пусть BD – x, тогда AD=c – x, CD=x.
x
x
3
4
2
6
1
8
T
5
Слайд 17
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
Решение
A
C
B
a
b
Искомую сторону
∆ABC обозначим c, то есть AB=c
Две стороны треугольника
равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b.c
B=, тогда C=2. Проведем CD – биссектрису C.
2
D
Рассмотрим ∆CBD – равнобедренный, так как BCD=B= (углы при основании ∆ABD) BD=CD.
Пусть BD – x, тогда AD=c – x, CD=x.
x
x
По теореме о биссектрисе внутреннего угла треугольника
3
4
5
2
1
8
T
6
Слайд 18
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
Доказательство
A
C
B
Пусть AD
– биссектриса ABC.
Так как площади треугольников, имеющих общую
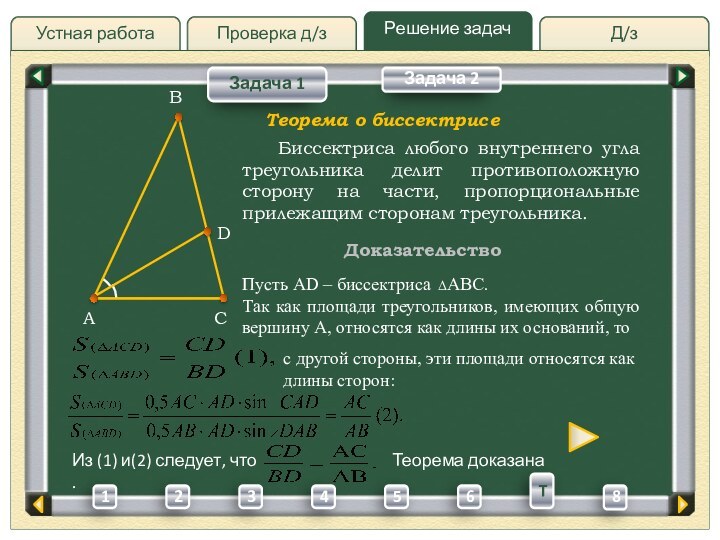
вершину A, относятся как длины их оснований, то Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
D
Теорема о биссектрисе
с другой стороны, эти площади относятся как
длины сторон:
Из (1) и(2) следует, что Теорема доказана .
3
4
5
2
6
1
8
T
Слайд 19
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
A
C
B
a
b
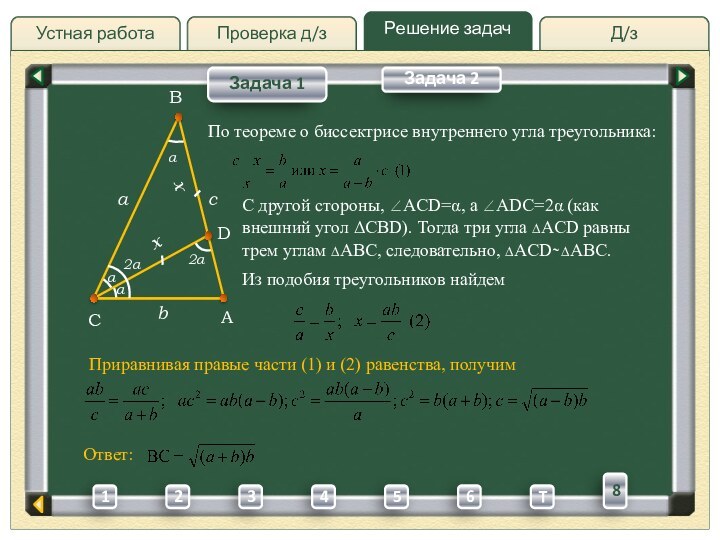
Из подобия
треугольников найдем
c
Приравнивая правые части (1) и (2) равенства, получим
2
D
x
x
По
теореме о биссектрисе внутреннего угла треугольника:С другой стороны, ACD=, a ADC=2 (как внешний угол CBD). Тогда три угла ∆ACD равны трем углам ∆ABC, следовательно, ∆ACD ̴ ∆ABC.
2
Ответ:
3
4
5
2
6
1
T
8
Слайд 20
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
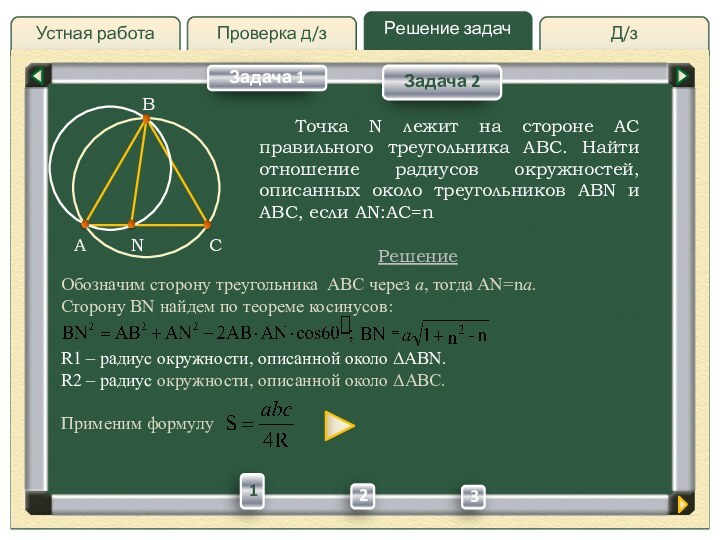
Точка N лежит на
стороне AC правильного треугольника ABC. Найти отношение радиусов окружностей,
описанных около треугольников ABN и ABC, если AN:AC=nРешение
Задача 1
Задача 2
B
A
C
N
Обозначим сторону треугольника ABC через а, тогда AN=na.
Сторону BN найдем по теореме косинусов:
R1 – радиус окружности, описанной около ABN.
R2 – радиус окружности, описанной около ABC.
Применим формулу
1
2
3
Слайд 21
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Около всякого треугольника можно
описать окружность, и притом только одну.
Задача 1
Задача 2
Центр окружности,
описанной около треугольника, лежит на пересечении перпендикуляров, восстановленных из середин сторон этого треугольника.Радиус R окружности, описанной около треугольника, по его сторонам и полупериметру вычисляется по формуле:
Также радиус R окружности, описанной около треугольника, может быть вычислен по формулам:
где S – площадь треугольника,
hc – высота, проведенная из вершины С.
3
2
1
Слайд 22
Д/з
Проверка д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
B
A
C
N
Применяя формулу
получим, что
Если у треугольников равны высоты, то их
площади относятся как основания. А так как ABN и ABC имеют общую высоту, проведенную из вершины B, то их площади относятся как длины оснований: Подставляя выражения для площадей, получим:
Ответ:
2
1
3
Слайд 23
Проверка д/з
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
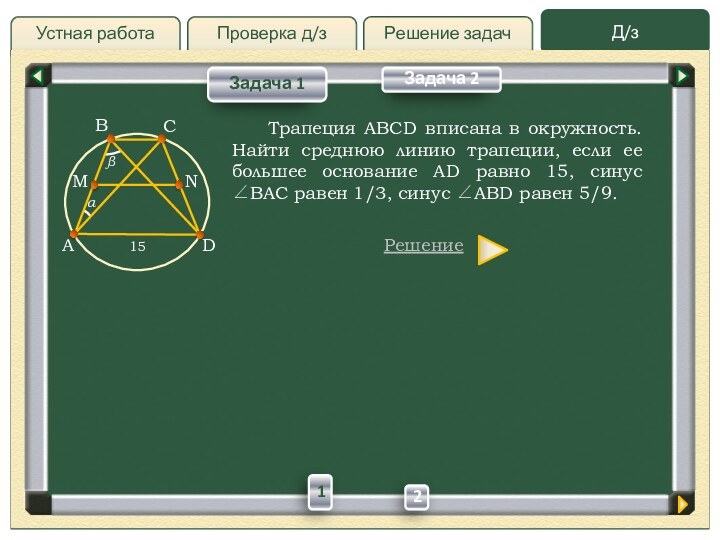
Трапеция ABCD
вписана в окружность. Найти среднюю линию трапеции, если ее
большее основание AD равно 15, синус BAC равен 1/3, синус ABD равен 5/9.Решение
M
A
D
B
C
N
15
1
2
Слайд 24
Проверка д/з
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 1
Задача 2
M
A
D
B
C
N
15
Решение
Средняя
линия трапеции равна
Для нахождения средней линии надо найти длину
основания BC.Используя свойства вписанных и центральных углов окружности, а также радиус описанной окружности R, выразим:
Длина
Ответ: 12
2
1
Слайд 25
Проверка д/з
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 2
Задача 2
Задача 1
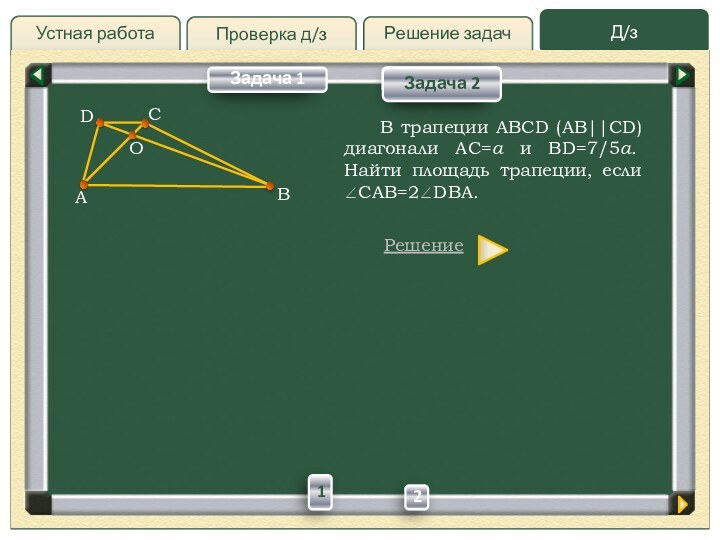
В
трапеции ABCD (AB||CD) диагонали AC=a и BD=7/5a. Найти площадь
трапеции, если CAB=2DBA.Решение
A
D
B
C
О
1
2
Слайд 26
Проверка д/з
Д/з
Решение задач
Устная работа
Проверка д/з
Задача 2
Задача 2
Задача 1
A
D
B
C
О
E
Решение
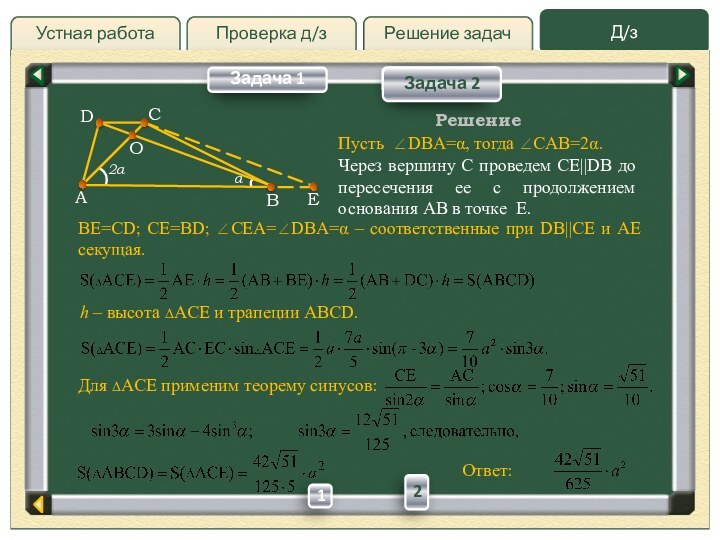
Пусть
DBA=, тогда CAB=2.
BE=CD; CE=BD; CEA=DBA= – соответственные при
DB||CE и AE секущая.Ответ:
Через вершину C проведем CE||DB до пересечения ее с продолжением основания AB в точке E.
2
h – высота ACE и трапеции ABCD.
Для ACE применим теорему синусов:
2
1