Слайд 2
ЭЛЛИПС
Возьмите плотный лист бумаги.
Прикрепите к нему в
двух точках нитку.
И натяните карандашом эту нитку.
Нарисуйте линию, двигая карандаш и
натягивая нитку. Получите эллипс.
Слайд 3
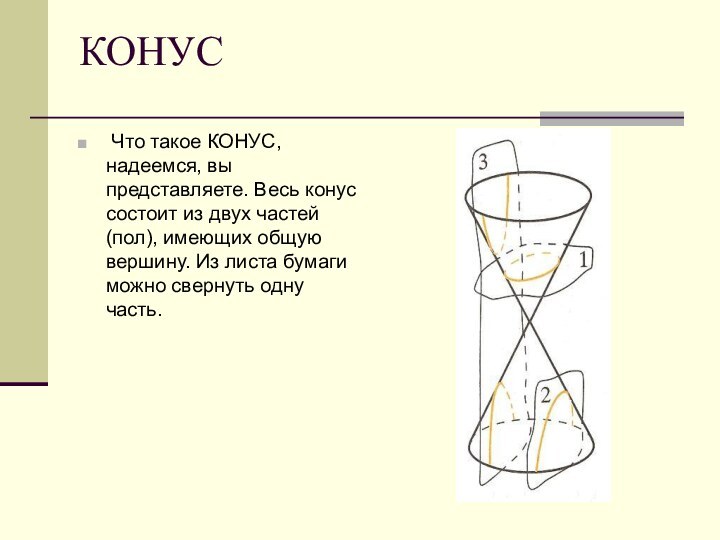
КОНУС
Что такое КОНУС, надеемся, вы представляете. Весь
конус состоит из двух частей (пол), имеющих общую вершину.
Из листа бумаги можно свернуть одну часть.
Слайд 4
ГИПЕРБОЛА
Используя определение гиперболы, нетрудно изготовить простейший прибор
для её вычерчивания. Нужно взять линейку, нить и три
кнопки. Две кнопки воткнуть в лист бумаги (рис) – и в этих точках будут фокусы гиперболы – и к ним привязать концы нити. Третью кнопку втыкают в линейку около её края, привязав к ней нить недалеко от середины нити, но не в середине. Если теперь, прижимая нить к краю линейки кончиком карандаша и держа нить всё время в натянутом состоянии, двигать карандаш, то её графит будет вычерчивать на бумаге одну из ветвей гиперболы. Заметим, что если нить привязать к третьей кнопке ровно в середине нити то гипербола вырождается в прямую – срединный перпендикуляр отрезка F1F2.
Слайд 5
ПАРАБОЛА
Парабола – одно из конических сечений. Эту кривую

можно определить как фигуру состоящую из всех точек М
плоскости, расстояние которых до заданной точки F, называемой фокусом параболы, равно расстоянию до заданной прямой L , называемой директрисой параболы (рис). Ближайшая к директрисе точка параболы называется вершиной параболы; прямая, проходящая через фокус перпендикулярно директрисе, - это ось симметрии параболы. Её называют просто осью параболы.
Определение параболы наводит на идею конструкции чертёжного пробора, способного вычерчивать параболу. На листе бумаги (рис) нужно закрепить линейку (её край будет директрисой будущей параболы), в точке F, которая станет фокусом параболы, булавкой прикрепить конец нити, другой конец которой закрепить в вершине острого угла чертёжного треугольника, притом так, чтобы длина нити равнялась катету этого треугольника. Перемещая второй катет вдоль линейки, и прижимая нить остриём карандаша к первому катету треугольника, мы получим кривую, точки которой находятся на Одинаковом расстоянии от края линейки и от точки F, т.е. параболу.
Слайд 6
СПИРАЛЬ АРХИМЕДА
Пусть по радиусу равномерно вращающегося
диска с постоянной скоростью ползет муравей. Проползая вперед, он
одновременно смещается в сторону вращения диска.
Слайд 7
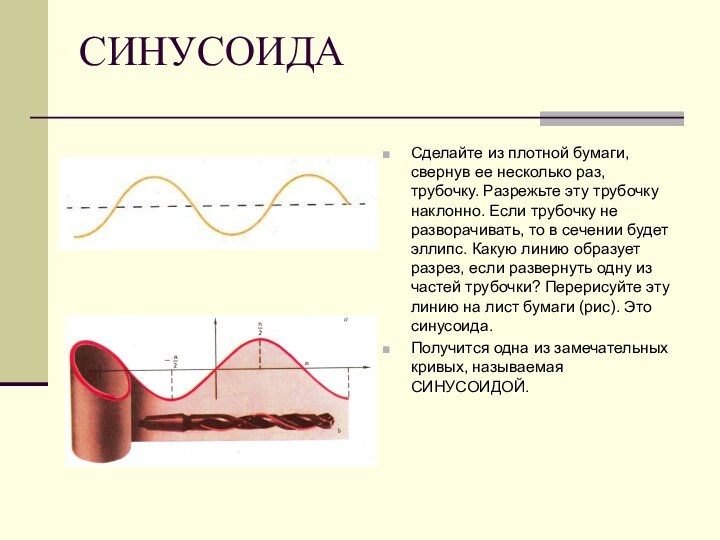
СИНУСОИДА
Сделайте из плотной бумаги, свернув ее несколько раз,
трубочку. Разрежьте эту трубочку наклонно. Если трубочку не разворачивать,
то в сечении будет эллипс. Какую линию образует разрез, если развернуть одну из частей трубочки? Перерисуйте эту линию на лист бумаги (рис). Это синусоида.
Получится одна из замечательных кривых, называемая СИНУСОИДОЙ.
Слайд 8
ЦИКЛОИДА
Представьте, что по прямой линии без скольжения катится
круг. Проследите за траекторией, которую опишет при этом точка
А, взятая на окружности этого круга (рис. а). Начертите получившуюся кривую.
ТЕОРИЯ: Она называется ЦИКЛОИДОЙ (рис.). Циклоида обладает многими замечательными свойствами. Вот одно из них. Давно математики пытались решить такую задачу: какой формы должен быть гладкий желоб, соединяющий две точки А и В (А выше, чем В), чтобы гладкий металлический шарик скатился по этому желобу из точки А в точку В под действием своего веса за кратчайшее время? Можно подумать, что желоб должен быть прямолинейным. Но это не так. Может быть, желоб следует выгнуть по дуге окружности, как думал великий итальянский физик, астроном и математик Галилео Галилей, живший на рубеже XVI-XVII вв.? Нет, Галилей ошибался. Только в 1696 г. швейцарский математик Иоганн Бернулли установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз (рис. в).
Слайд 9
ГИПОЦИКЛОИДА
Возьмите кусок толстого картона и вырежьте в нем
круг радиусом 12 см. Из того же материала вырежьте
три круга радиусами 4 см, 3 см и 2 см. Положите кусок картона с вырезанным в нем отверстием на лист бумаги, вложите в этот вырез первый из трех кружков, чтобы он касался края, и отметьте на окружности маленького круга точку (рис. а). Проследите за тем, какую линию опишет отмеченная точка, когда кружок катится по окружности выреза без скольжения. Проделайте то же самое со вторым и третьим кругами.
ТЕОРИЯ: Получившиеся линии – ГИПОЦИКЛОИДЫ (рис.б). Все кривые, которые вычерчивает точка на окружности, катящейся внутри другой окружности, принадлежит семейству гипоциклоид (от греческого «гипо» - «под», «внизу» и «киклоидес» - «кругообразный»).
ЗАДАНИЕ НА САМОСТОЯТЕЛЬНОЕ РЕШЕНИЕ: о что превратится гипоциклоида, если радиус меньшего круга равен 6 см, а большего – 12 см? Как выглядит гипоциклоида для кругов с радиусом 8 см, 9 см и 10 см?