Презентация на тему Конус, его элементы и формулы

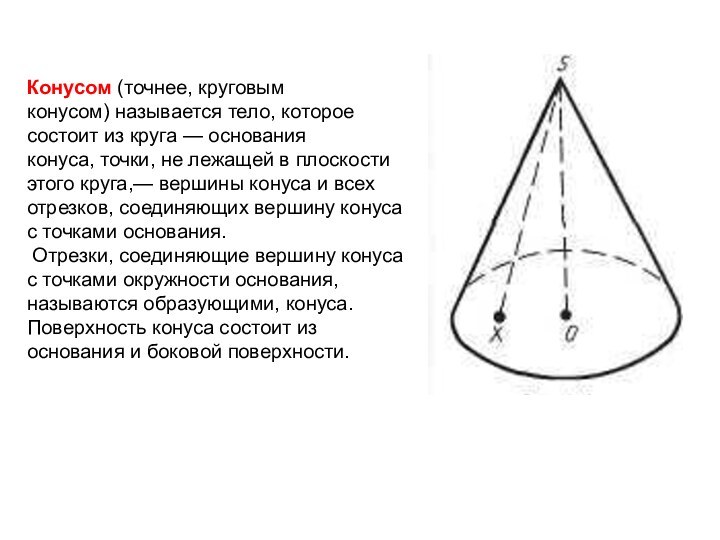
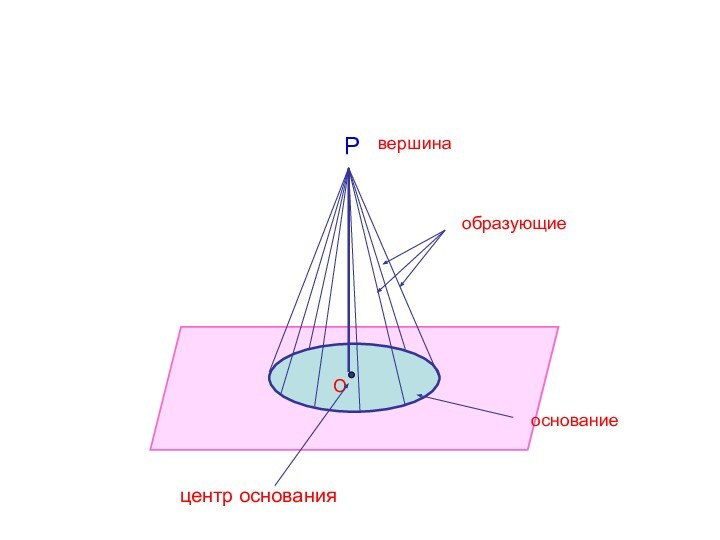
круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины

конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.

центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем

рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту. 

собой равнобедренный треугольник, у которого боковые стороны являются образующими

конуса (рис. 3).

В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4).

(рис. 3).

(рис. 4)

меньший конус. Оставшуюся часть называют усеченным конусом. Усеченный конус можно

получить и как тело вращения.
Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.
Круги O и O1 - его основания, его образующие AA1 равны между собой, прямая OO1 - ось, отрезок OO1 - высота. Его осевое сечение - равнобедренная трапеция.

по кругу, а боковую поверхность  - по окружности с

центром на оси конуса.

Доказательство. Пусть   - плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость     с плоскостью основания, совмещает сечение конуса плоскостью     с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. 
Теорема доказана.

(рис.5)

R_{2}) \cdot l $$

Объем усеченного конуса: 
$$V = \frac{1}{3}\pi H(R^{2}_{1}

+ R_{1} \cdot R_{2} + R^{2}_{2})$$,

где h - высота усеченного конуса; R1,R2 - радиусы верхнего и нижнего оснований; l - образующая.

выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки,

гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
«Конусами» называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры.