объектами: прямыми , плоскостями и телами
Знакомство с новым понятием:
расстояние между скрещивающимися прямымиУсвоение и отработка общих приемов определения расстояний между скрещивающимися прямыми
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Расстояние между скрещивающимися прямыми
Содержание
- 2. Цели: Систематизация и обобщение приемов работы с
- 3. Задачи: Устная работа по актуализация необходимых известных
- 4. Средства: Модели пространственных фигур, чертежи к задачамТеорема
- 5. План: Первый урок: Актуализация: выполнение устных заданий,
- 6. Первый урокПодготовительные устные задачиMKLNПараллельны ли прямая B1K
- 7. Первый урокПодготовительные устные задачиMKLNУстановите все пары: прямая и параллельная ей плоскость
- 8. Первый урокПодготовительные устные задачиMKLNКак определяется расстояние между
- 9. Первый урокПостановка проблемыKLКак можно определить расстояние между
- 10. Первый урокКакие следствия можно сформулировать?KLОтрезок с концами
- 11. Первый урокТеоремаOДиагональ куба перпендикулярна каждой диагонали грани
- 12. Первый урокСледствие теоремы. Задача.OMРассмотрим треугольники BB1D и
- 13. Второй урокОбобщение.Три типовых случая определения расстояния между
- 14. Второй урокПроблема: Как найти плоскость с одной
- 15. Второй урокТиповые задачиЧаще других возникают задачи с
- 16. Второй урокРешение задачДан куб ABCDA1B1C1D1 с длиной
- 17. Второй урокРешение задачДан куб ABCDA1B1C1D1 с длиной
- 18. Второй урокПрием параллельных плоскостейДан куб ABCDA1B1C1D1 с
- 19. Второй урокПрием параллельных плоскостейO1KMOMNРассмотрим сечение куба плоскостью
- 20. Третий урокОбобщение приемов определения расстояний между скрещивающимися
- 21. Третий урокЗадача на обобщение приема Проведем через
- 22. Третий урокЗадача на обобщение приема ABCMDKNВычислим длину
- 23. Третий урокРефлексия. Осмысление обобщенного приема Рассмотренный способ
- 24. Третий урокОриентировочная основа обобщенного приема Первый этап:
- 25. Третий урокКак найти точки на скрещивающихся прямых
- 26. Третий урокЗадача на закрепление обобщеннного способаВ кубе
- 27. Скачать презентацию
- 28. Похожие презентации
Цели: Систематизация и обобщение приемов работы с пространственными объектами: прямыми , плоскостями и теламиЗнакомство с новым понятием: расстояние между скрещивающимися прямымиУсвоение и отработка общих приемов определения расстояний между скрещивающимися прямыми
Слайд 2
Цели:
Систематизация и обобщение приемов работы с пространственными
объектами: прямыми , плоскостями и телами
расстояние между скрещивающимися прямымиУсвоение и отработка общих приемов определения расстояний между скрещивающимися прямыми
Слайд 3
Задачи:
Устная работа по актуализация необходимых известных приемов
работы с пространственными объектами: прямыми и плоскостями
Определение нового понятия:
расстояние между скрещивающимися прямымиРешение типовых задач на определение расстояний между скрещивающимися прямыми
Решение проблемной задачи на обобщение приема нахождения расстояния между скрещивающимися прямыми
Слайд 4
Средства:
Модели пространственных фигур, чертежи к задачам
Теорема Фалеса
и теорема о трех перпендикулярах
Приемы стерео и планиметрических
построенийТиповые и проблемные задачи
Компьютер с мультимедийным проектором
Слайд 5
План:
Первый урок:
Актуализация: выполнение устных заданий, доказательство
теоремы, решение задачи
Определение и усвоение нового понятия
Второй
урок . Решение типовых задач на усвоение и отработку нового понятияТретий урок. Проблемная задача на обобщение приема нахождения расстояния между двумя скрещивающимися прямыми
Слайд 6
Первый урок
Подготовительные устные задачи
M
K
L
N
Параллельны ли прямая B1K и
плоскость DD1C1C?
Параллельны ли прямые C1D и B1K?
Параллельны ли прямая
AC и плоскость A1B1C1D1?Параллельны ли прямая AL и плоскость A1B1C1D1?
Слайд 7
Первый урок
Подготовительные устные задачи
M
K
L
N
Установите все пары: прямая и
параллельная ей плоскость
Слайд 8
Первый урок
Подготовительные устные задачи
M
K
L
N
Как определяется расстояние между прямой
и параллельной ей плоскостью?
Найдите расстояние между прямой MN и
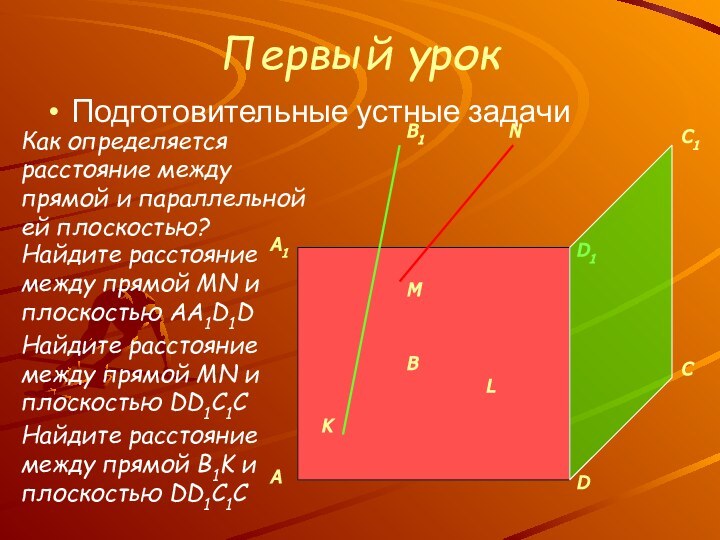
плоскостью AA1D1DНайдите расстояние между прямой MN и плоскостью DD1C1C
Найдите расстояние между прямой B1K и плоскостью DD1C1C
Слайд 9
Первый урок
Постановка проблемы
K
L
Как можно определить расстояние между скрещивающимися
прямыми ?
K1
L1
Найдите расстояние между прямыми:
A1B и C1D,
A1B
и DK ,A1B и DL.
Слайд 10
Первый урок
Какие следствия можно сформулировать?
K
L
Отрезок с концами на
двух скрещивающихся прямых одновременно перпендикулярный им и есть расстояние
между этими прямымиK1
L1
Этот отрезок равен расстоянию от одной из скрещивающихся прямых до параллельной ей плоскости в которой лежит другая прямая
Слайд 11
Первый урок
Теорема
O
Диагональ куба перпендикулярна каждой диагонали грани куба,
скрещивающейся с ней
Доказательство: AC⊥BB1D1D, отсюда AC ⊥ любой прямой
плоскости BB1D1D
Слайд 12
Первый урок
Следствие теоремы. Задача.
O
M
Рассмотрим треугольники BB1D и OMD.
Из их подобия следует OM/BB1=OD/B1D
OM=BB1⋅OD/B1D=a/√6
Найдите расстояние между скрещивающимися диагональю
куба и диагональю его грани. Решение. Треугольник BB1D перпендикулярен AC. Отрезок OM ⊥ B1D, будет перпендикулярен и AC . OM - расстояние между AC и B1D.
Слайд 13
Второй урок
Обобщение.Три типовых случая определения расстояния между скрещивающимися
прямыми
Общий перпендикуляр к обеим прямым (единственный!)
Перпендикуляр от одной из
прямых до параллельной плоскости, в которой расположена другая прямая, конец которого не обязательно лежит на прямой!Перпендикуляр между параллельными плоскостями в которых лежат скрещивающиеся прямые, концы которого не обязательно лежат на прямых!
Слайд 14
Второй урок
Проблема: Как найти плоскость с одной прямой,
параллельную другой скрещивающейся прямой ?
Достаточно провести через одну из
скрещивающихся прямых прямую линию, параллельную другой скрещивающейсяЗаметим, что отрезок соединяющий точки пересечения пар параллельных прямых не равен расстоянию между скрещивающимися прямыми!
Слайд 15
Второй урок
Типовые задачи
Чаще других возникают задачи с перпендикулярными
скрещивающимися прямыми.
К этому типу относится уже рассмотренная задача
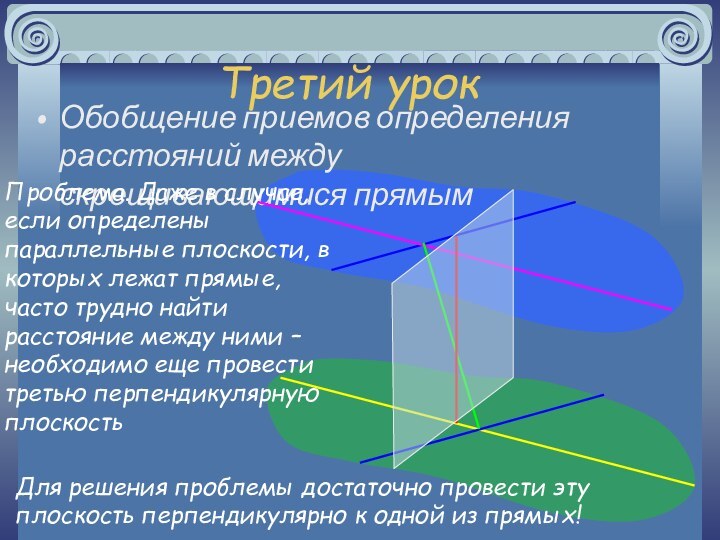
о расстоянии между диагональю куба и скрещивающейся диагональю его грани.Стандартный прием решения этих задач заключается в проведении плоскости, в которой лежит одна прямая, перпендикулярно другой скрещивающейся прямой
Слайд 16
Второй урок
Решение задач
Дан куб ABCDA1B1C1D1 с длиной ребра
AB=a. Найдите расстояние между прямыми AD и D1 M,
где M – середина ребра DCПлоскость грани DD1C1C перпендикулярна ребру AD. Из точки D опустим перпендикуляр DK на D1 M. Треугольники DD1M и DKM подобны с коэффициентом подобия 1/2. DK=D1M/2=a⋅√5/2
M
K
Слайд 17
Второй урок
Решение задач
Дан куб ABCDA1B1C1D1 с длиной ребра
AB=a. Найдите расстояние между прямыми BD и O1 M,
где M – середина AO, O и O1 – центры граней ABCD и A1B1C1D1, соответственноДиагональная плоскость AA1C1C перпендикулярна прямой BD. Из точки O опустим перпендикуляр OK на O1 M. Треугольники OO1M и OKM подобны. OK=OO1⋅OM/O1M =a/3 (по теореме Пифагора O1M=3/2√2, OM=1/2√2)
O1
K
M
O
Слайд 18
Второй урок
Прием параллельных плоскостей
Дан куб ABCDA1B1C1D1 с длиной
ребра AB=a. Найдите расстояние между скрещивающимися диагоналями AC и
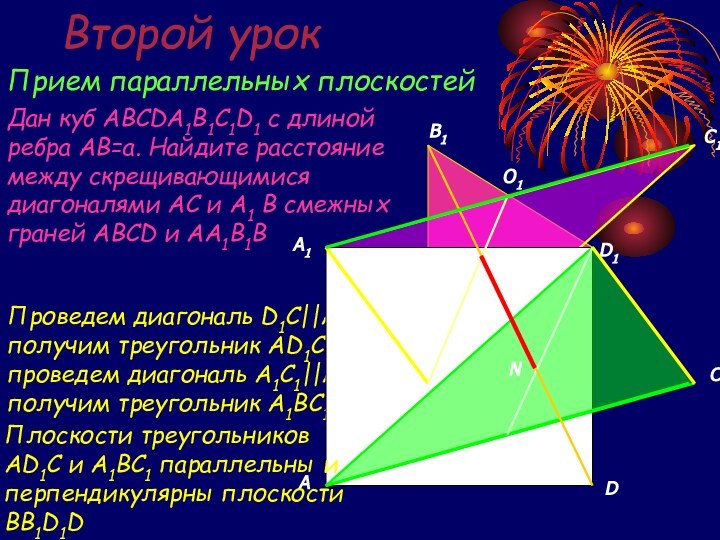
A1 B смежных граней ABCD и AA1B1BПроведем диагональ D1C||A1B, получим треугольник AD1C||A1B, проведем диагональ A1C1||AC, получим треугольник A1BC1||AC
O1
K
M
O
M
N
Плоскости треугольников AD1C и A1BC1 параллельны и перпендикулярны плоскости BB1D1D
Слайд 19
Второй урок
Прием параллельных плоскостей
O1
K
M
O
M
N
Рассмотрим сечение куба плоскостью BB1D1D.
Искомое расстояние MN по теореме Фалеса равно 1/3 диагонали
B1D: MN=a/√3M
N
B
B1
D1
D
O1
O
Замечание. Перпендикулярность B1D к B1O и OD1 следует из доказанной теоремы на первом уроке.
Слайд 20
Третий урок
Обобщение приемов определения расстояний между скрещивающимися прямым
Проблема. Даже в случае, если определены параллельные плоскости, в
которых лежат прямые, часто трудно найти расстояние между ними –необходимо еще провести третью перпендикулярную плоскостьДля решения проблемы достаточно провести эту плоскость перпендикулярно к одной из прямых!
Слайд 21
Третий урок
Задача на обобщение приема
Проведем через точку
A прямую параллельную BM. Из точки B опустим на
неё перпендикуляр BK.A
B
C
M
D
K
N
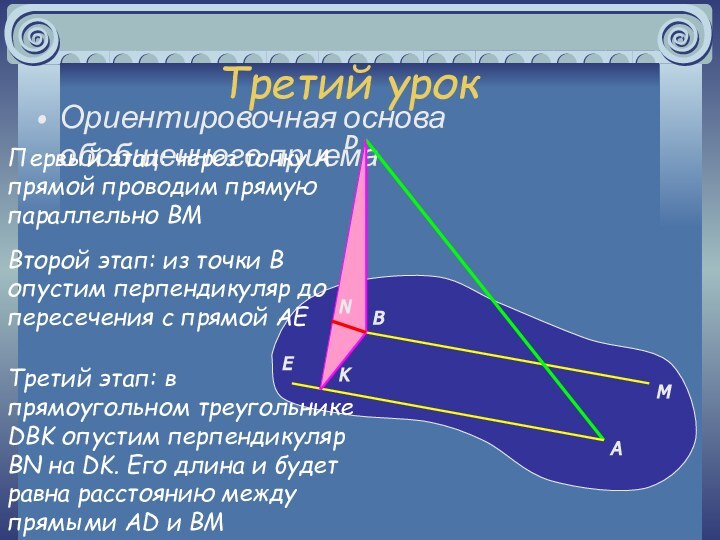
По теореме о трех перпендикулярах DK ⊥ AK и треугольник DBK ⊥ треугольнику ADK , в которой лежит прямая AD.
Прямая BM находится на расстоянии BN от плоскости ADK, равном длине перпендикуляра BN к DK!
Слайд 22
Третий урок
Задача на обобщение приема
A
B
C
M
D
K
N
Вычислим длину отрезка
BN через площадь DBK и длину DK.
SDBK =a2/4,
DK=√5∙a/2, BN=2⋅ SDBK /DK BN=a/ √5
Слайд 23
Третий урок
Рефлексия. Осмысление обобщенного приема
Рассмотренный способ последней
задачи носит обобщенный характер.
Если не проходят более элементарные приемы,
то последний способ часто оказывается решающим.A
B
M
D
Идея этого приема связана с двумя дополнительными объектами: а) плоскостью, в которой лежит одна из прямых. б) перпендикуляром к ней, через который проходит вторая прямая.
Запомните последнюю картинку!
Слайд 24
Третий урок
Ориентировочная основа обобщенного приема
Первый этап: через
точку A прямой проводим прямую параллельно BM
A
B
M
D
Второй этап: из
точки B опустим перпендикуляр до пересечения с прямой AEE
K
Третий этап: в прямоугольном треугольнике DBK опустим перпендикуляр BN на DK. Его длина и будет равна расстоянию между прямыми AD и BM
N
Слайд 25
Третий урок
Как найти точки на скрещивающихся прямых AD
и BM, ближайшие друг к другу?
Через точку N
проводим прямую параллельно BM до пересечения с прямой AD в точке L (в плоскости треугольника ADK).A
B
M
D
E
K
Прямоугольный треугольник DBK переносим параллельно вдоль прямой на отрезок NL. Новые положения точек B и N будут ближайшими друг к другу точками прямых AD и BM
N
L
Слайд 26
Третий урок
Задача на закрепление обобщеннного способа
В кубе с
длиной ребра a=5 на ребрах AD и D1C взяты
точки K и M, соответственно. Найдите расстояние между прямыми A1K и D1M, если AK=4 и DM=3.M
K
E
H
N
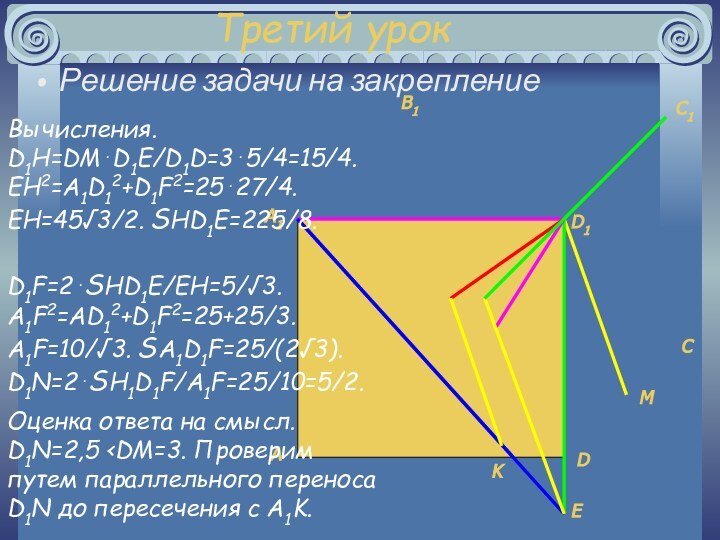
Решение. Через точку E пересечения A1K c D1D проведем прямую || D1M. Из точки D1 на неё опустим перпендикуляр до пересечения в точке F. Высота D1N треугольника A1D1F и дает искомое расстояние.
F
