Презентация на тему по геометрии Пифагор и его знаменитая теорема (8 класс)

ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто

в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина это :

КРАСОТА

ПРОСТОТА

ЗНАЧИМОСТЬ

имеет огромное значение: она применяется в геометрии буквально на

каждом шагу, а так же является основой всех математических вычислений, расчетов и многих изобретений. Разработка творческого проекта полезна еще и потому, что в современных школьных учебниках дается алгебраическое доказательство теоремы. При этом бесследно исчезает первозданная геометрическая аура теоремы, которая вела древних мудрецов к истине, а путь этот почти всегда оказывался кратчайшим и всегда красивым.

значение теоремы Пифагора в развитии науки и техники многих

стран и народов мира, а также в наиболее простой и интересной форме преподать содержание теоремы.

различных способов существующих доказательств теоремы.

Определение значения теоремы Пифагора для

развития науки и использования в различных областях.

Работа с литературой, в сети Интернета.

Умение обобщать и обрабатывать полученную информацию.

метод систематизации и обработки данных.
В данном проекте будут подробно

разобраны: биография Пифагора, история создания теоремы и рассмотрены некоторые классические доказательства теоремы Пифагора, известные из древних трактатов.

490 года до н.э.) Пифагор в Сидоне Финикийском. Факты

биографии Пифагора не известны достоверно. О его жизненном пути можно судить лишь из произведений других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учеными того времени.
Как математик Пифагор достиг больших успехов. Ему приписывают открытие и доказательство теоремы Пифагора, создание таблицы Пифагора. Известно, что члены его ордена занимались космологией, верили в переселение душ. Философское учение Пифагора можно разделить на две части – научную и религиозную.

жизни
научный подход к постижению мира

культа, запрещающего есть бобы. Фактически Пифагор создал тайное общество,

ставившее перед собой не только политические цели, но и работавшее над нравственным и физическим очищением. В частности, пифагорейцы считали, что душа переселяется с небес в тело животного или человека, пока не заслужит права снова вернуться на небо.
Среди заслуг пифагорейцев стоит выделить пропагандирование идеи о количественных закономерностях развития мира. Пифагор считал, что в основе мироздания лежит число. По его мнению, познание мира состоит в познании управляющих им чисел. В результате пифагорейцы разработали различные числовые отношения во многих областях человеческой деятельности.

космологом, но в ранних источниках не упоминается о таких

его заслугах. К примеру, Ямвлих пишет, что пифагорейцы часто приписывали собственные открытия Пифагору. В частности, философу отдают авторство известной теоремы. Но многие современные исследователи придерживаются мнения, что Пифагор не доказывал данную теорему, а просто передал знание, известное в Вавилоне задолго до его рождения. Некоторые приписывают Пифагору открытие того, что Земля — шар. Но Диоген Лаэртский утверждает, что такое суждение высказывал Анаксимандр Милетский, который учил Пифагор в юности. Тем не менее, научные заслуги пифагорейской школы в космологии и математике бесспорны.

Утверждение, гласящее, что квадрат гипотенузы равен сумме квадратов катетов,

было известно еще задолго до рождения греческого математика.

Однако теорема Пифагора, история создания и доказательства ее связываются для большинства именно с этим ученым. Согласно некоторым источникам, причиной тому послужило первое доказательство теоремы, которое было приведено Пифагором. Однако часть исследователей опровергает этот факт.

соотношение между гипотенузой и катетами прямоугольного треугольника.
Рассмотрим прямоугольный треугольник

с катетами a, b и гипотенузой с. Докажем, что c² = a² + b²

Достроим треугольник до квадрата со стороной a + b.
Площадь этого квадрата равна
(a + b)² С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна  
2ab + c², и квадрата со стороной с, поэтому S = 4 × +c² = 2ab + c²
Таким образом, (a + b)² =2ab + c² откуда c² = a² + b²
Теорема доказана.

выяснила, что можно применить подобие треугольников к доказательству теоремы

Пифагора. А именно, я воспользовалась утверждением о том, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.

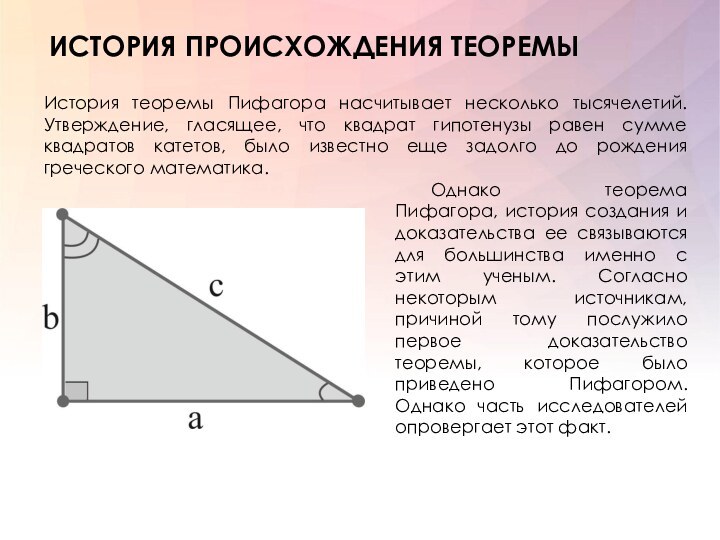
Рассмотрим прямоугольный треугольник с прямым углом C, CH– высота. Докажем, что AC² + CB² = AB²
На основании утверждения о катете прямоугольного треугольника:

Возведем в квадрат и сложим полученные равенства:
AC²=AB×AH, CB²=AB×HB;
AC²+CB²=AB×(AH+HB),где AH+HB=AB
АС² + СВ² = АВ × АВ,
АС² + СВ² = АВ².
Доказательство закончено.