- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площадь криволинейной трапеции и интеграл
Содержание
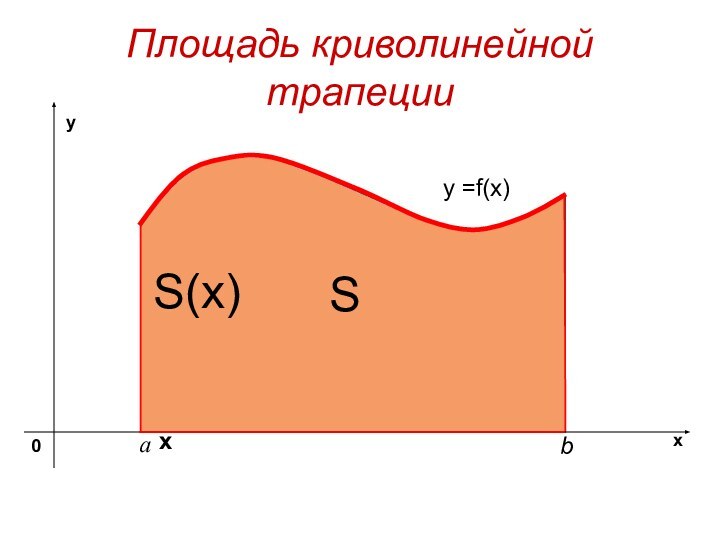
- 2. Площадь криволинейной трапецииy =f(x) SхS(x)
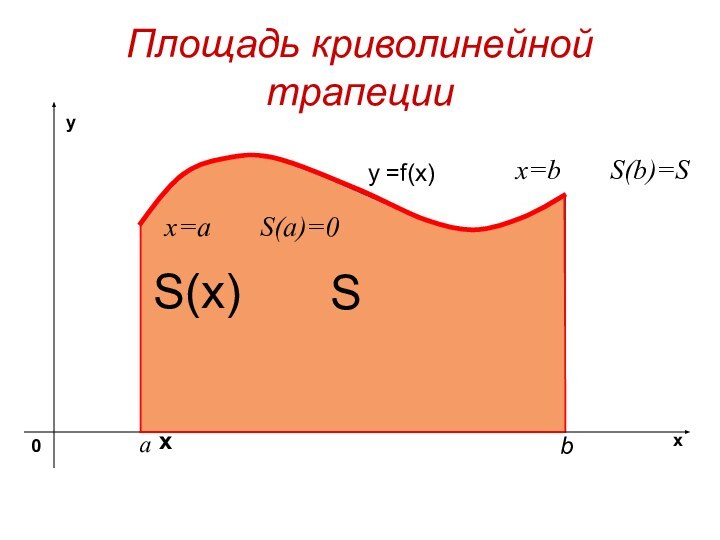
- 3. Площадь криволинейной трапецииy =f(x) SхS(x)x=a S(a)=0x=b S(b)=S
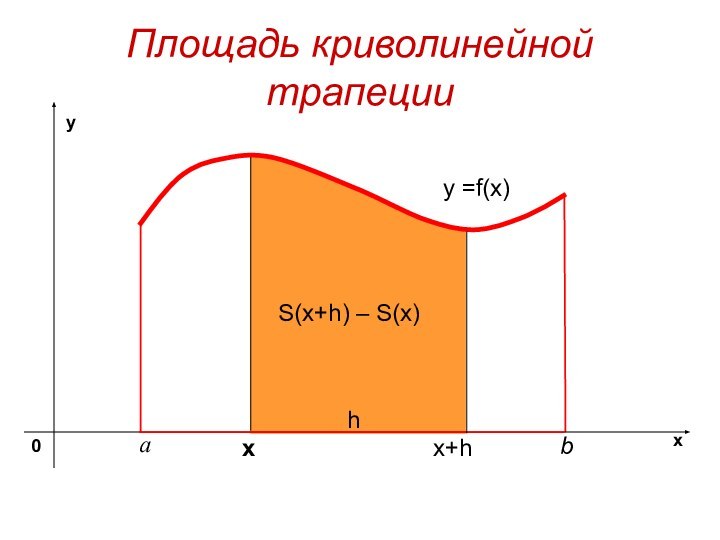
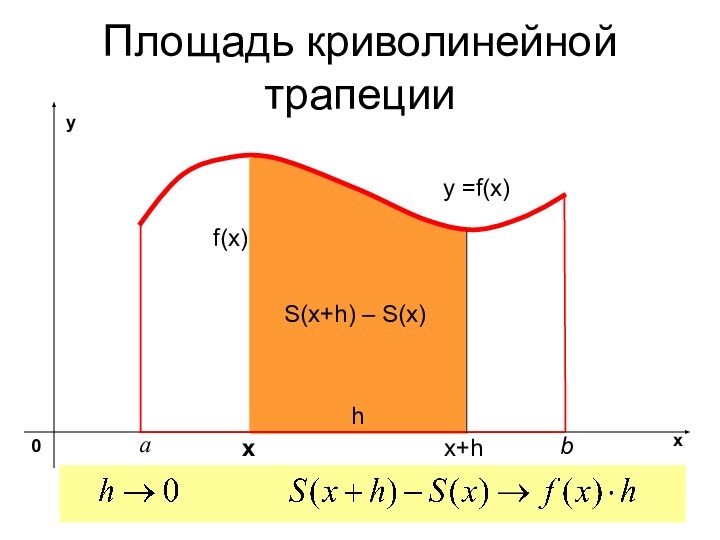
- 4. Площадь криволинейной трапецииy =f(x) хS(x+h) – S(x)x+hh
- 5. Площадь криволинейной трапецииy =f(x) хS(x+h) – S(x)x+hhf(x)
- 6. Площадь криволинейной трапеции
- 7. Фигура, ограниченная снизу отрезком [a, b]
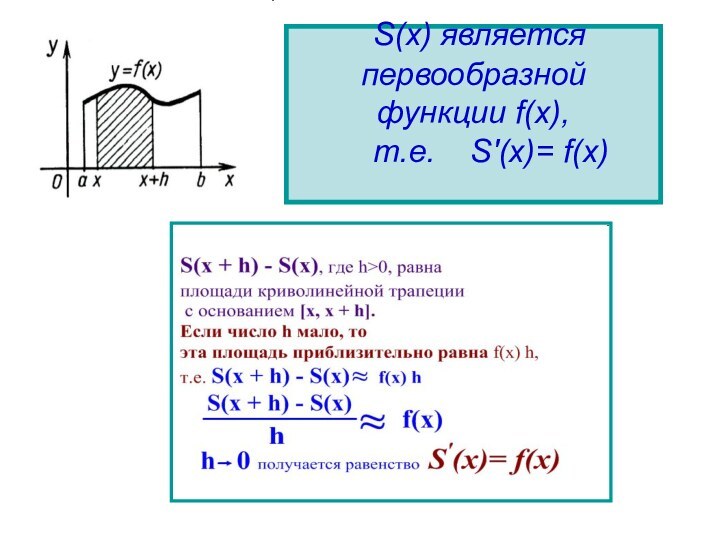
- 8. Обозначим S(х) - площадь криволинейной трапеции с
- 9. S(х) является первообразной функции f(x), т.е. S'(х)= f(x)
- 10. Площадь криволинейной трапеции
- 11. Любая другая первообразная F(x) отличается от
- 12. Немного истории -1675 г, опубликовано в 1686
- 13. Лейбниц Готфрид Вильгельм (1646-1716) « Общее
- 14. Исаак Ньютон (1643-1727)Разумом он превосходил род человеческий.
- 15. Немного истории «Интеграл» придумал Я.Бернулли (1690)«восстанавливать» от латинского integro«целый» от латинского integer
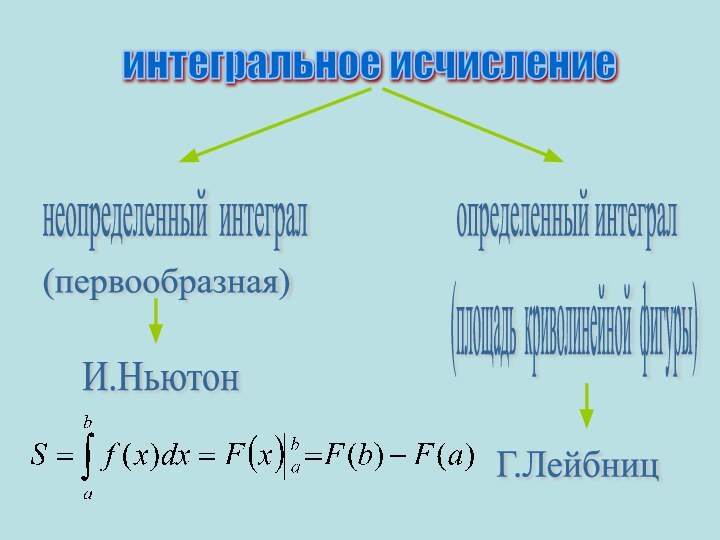
- 16. интегральное исчисление неопределенный интеграл определенный интеграл (первообразная) (площадь криволинейной фигуры) И.Ньютон Г.Лейбниц
- 17. Применение интеграла Площадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силыЦентр масс
- 18. В классе:№ 999(1,3)№ 1000(1,2)
- 19. Скачать презентацию
- 20. Похожие презентации
Площадь криволинейной трапецииy =f(x) SхS(x)


![Площадь криволинейной трапеции и интеграл Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной](/img/tmb/12/1141994/12c3c5c641c79de68a0919b4c4ccbcd2-720x.jpg)
![Площадь криволинейной трапеции и интеграл Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х] , х](/img/tmb/12/1141994/1bef270e2cead4212e51085838154df5-720x.jpg)









Слайд 7 Фигура, ограниченная снизу отрезком [a, b] оси
Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные
значения , а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.Слайд 8 Обозначим S(х) - площадь криволинейной трапеции с основанием
[a, х] ,
х - любая точка отрезка
[a, b] При х = а отрезок [a, х] вырождается в
точку, поэтому S(а) = 0; при х = b,
S(b) = S
Слайд 10 Площадь криволинейной трапеции
вычисляется по формуле S = F(b)
- F(a)Разность F(b) - F(a) называют
интегралом от функции f(x)
на отрезке [a, b] и обозначают так :
Слайд 11 Любая другая первообразная F(x) отличается от S(x) на
постоянную,
т.е. F(x) = S(x) + С
При х =
а получаем F(a) = S(a) + CТак как S(a) = 0 , то С = F(a) и равенство
F(x) = S(x) + С можно записать так
S(x) = F(x) - F(a), отсюда при х =b получим
S(b) = F(b) - F(a)
Слайд 12
Немного истории
-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц
-
1675 г, Ж Лагранж
5 век до н.э. др.гр. ученый
Демокрит3-4 век до н.э. Архимед ввел метод исчерпывания
Слайд 13
Лейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков
представляет чудесное пособие, так как оно разгружает воображение… Следует
заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»Лейбниц