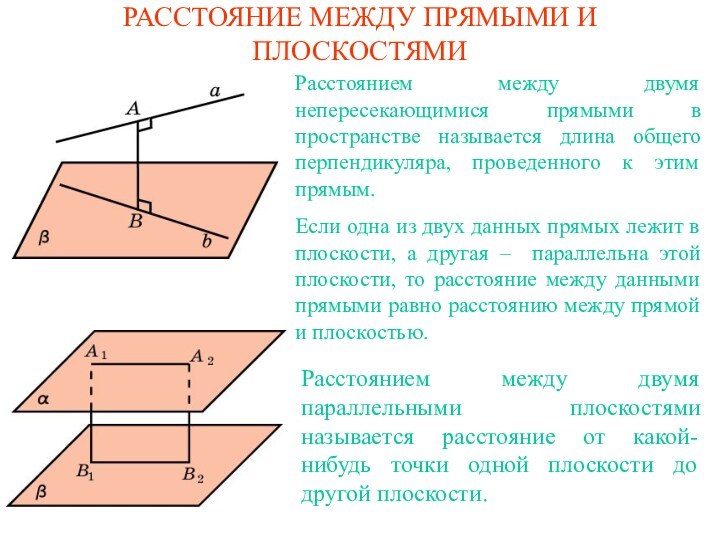
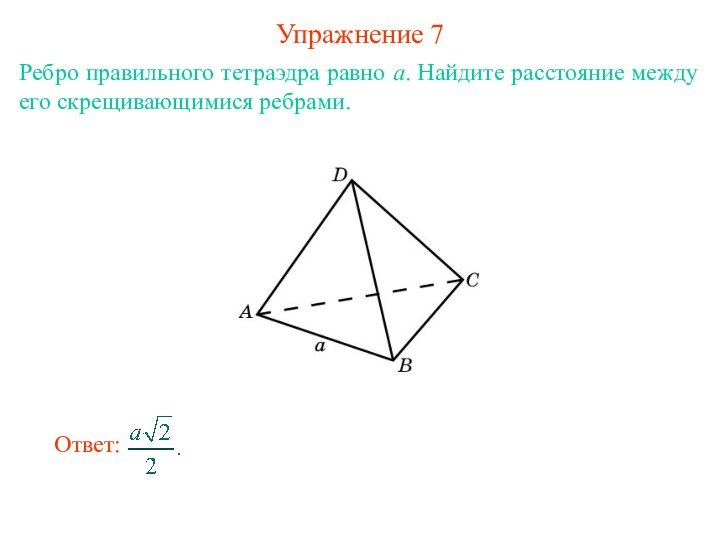
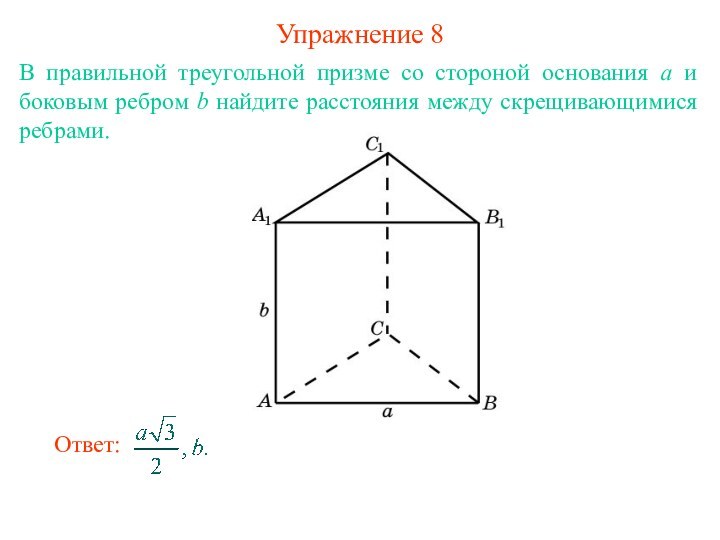
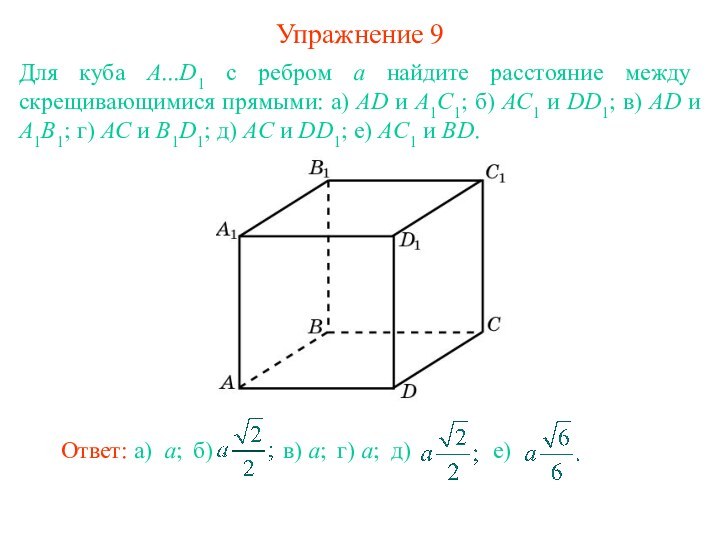
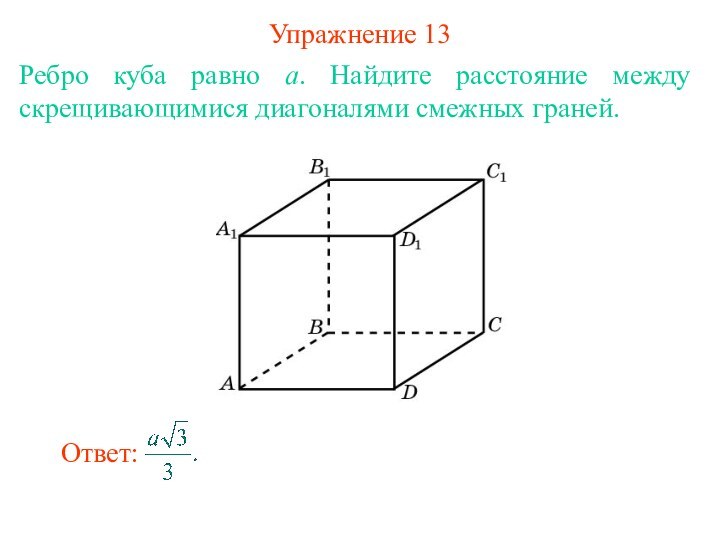
прямыми в пространстве называется длина общего перпендикуляра, проведенного к
этим прямым.Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.
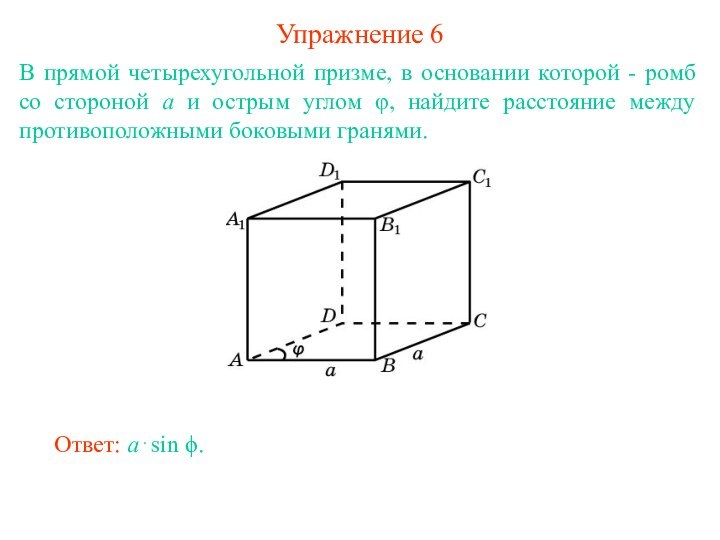
Расстоянием между двумя параллельными плоскостями называется расстояние от какой-нибудь точки одной плоскости до другой плоскости.