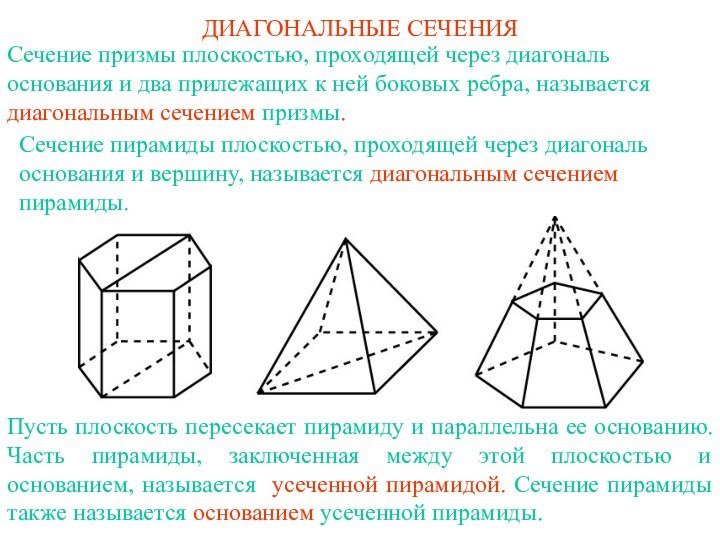
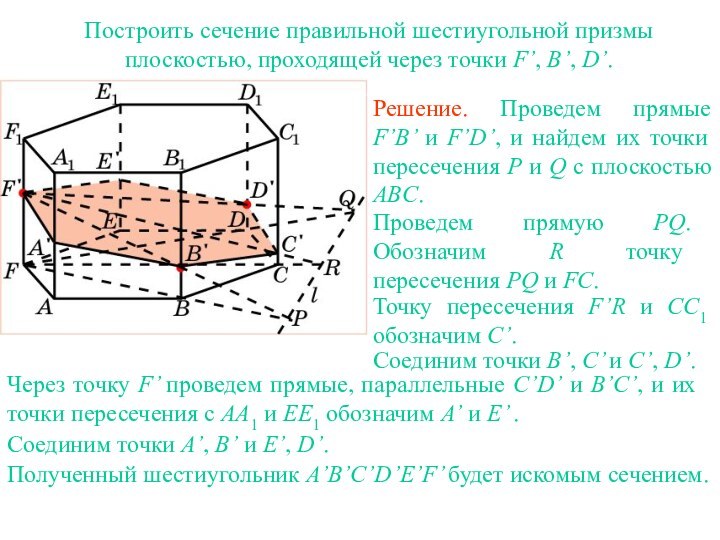
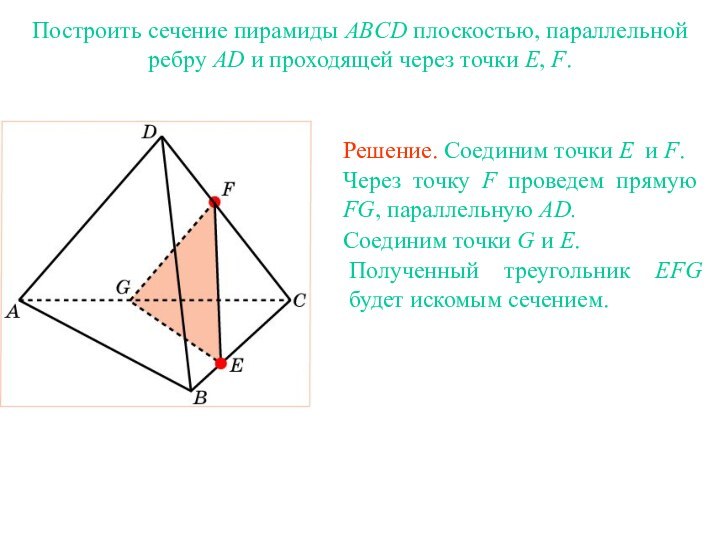
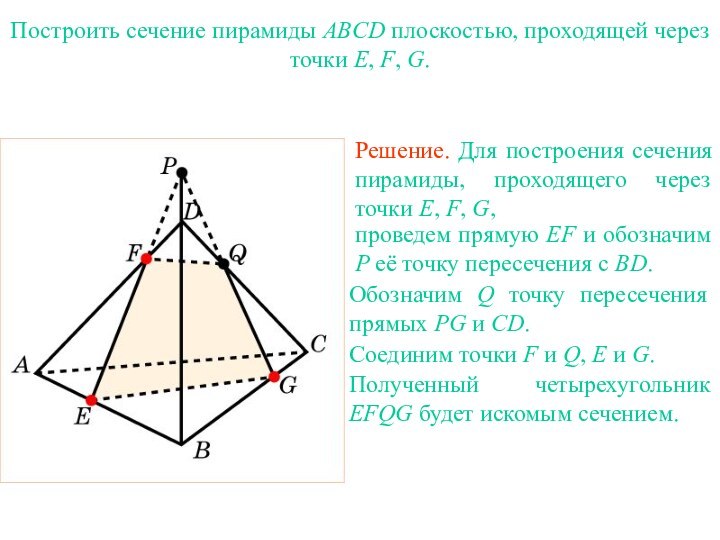
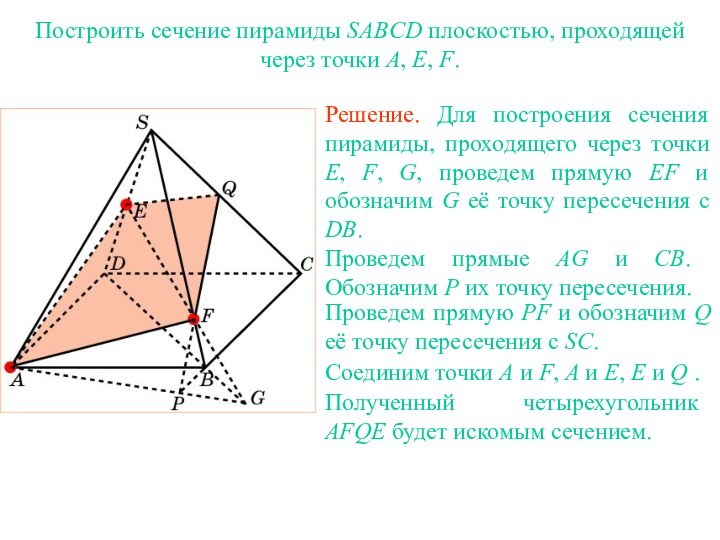
два прилежащих к ней боковых ребра, называется диагональным сечением
призмы.Сечение пирамиды плоскостью, проходящей через диагональ основания и вершину, называется диагональным сечением пирамиды.
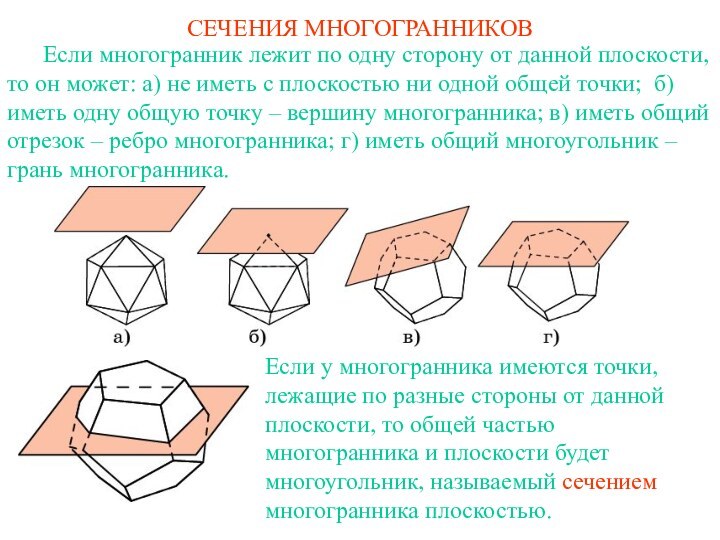
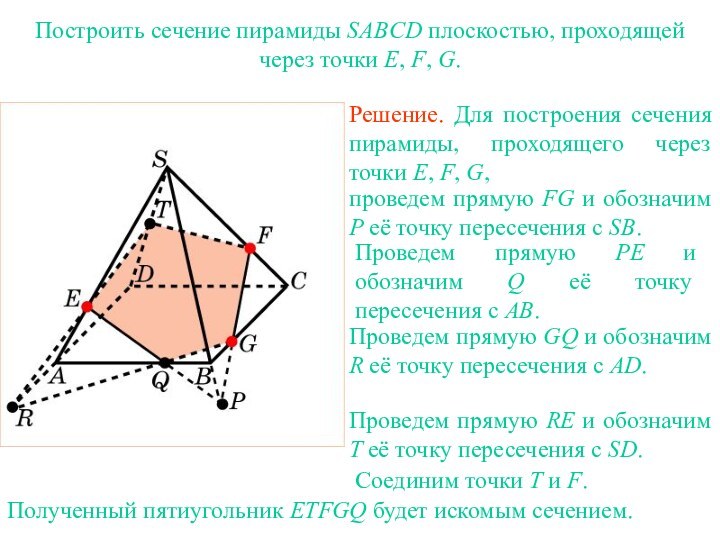
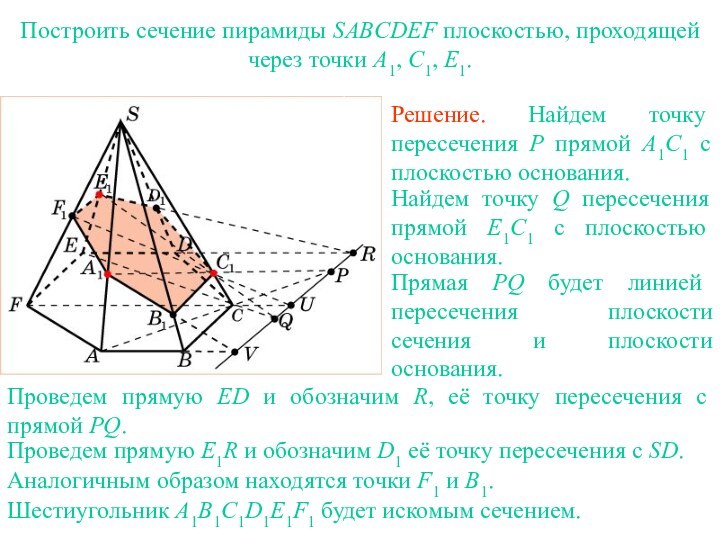
ДИАГОНАЛЬНЫЕ СЕЧЕНИЯ
Пусть плоскость пересекает пирамиду и параллельна ее основанию. Часть пирамиды, заключенная между этой плоскостью и основанием, называется усеченной пирамидой. Сечение пирамиды также называется основанием усеченной пирамиды.