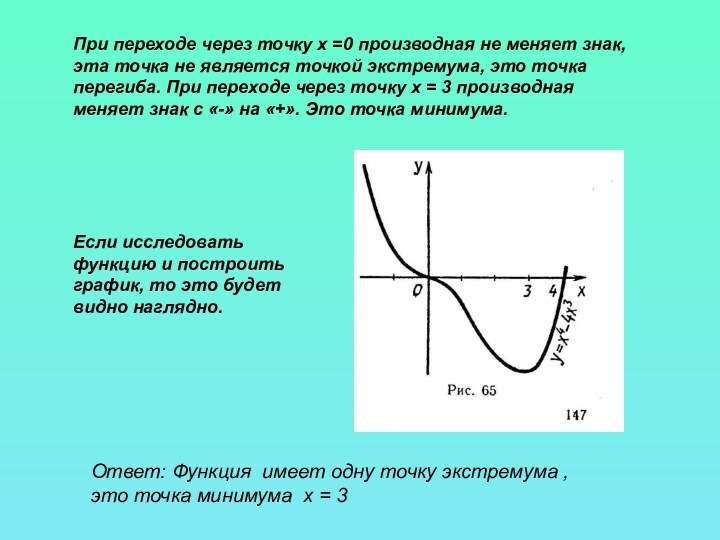
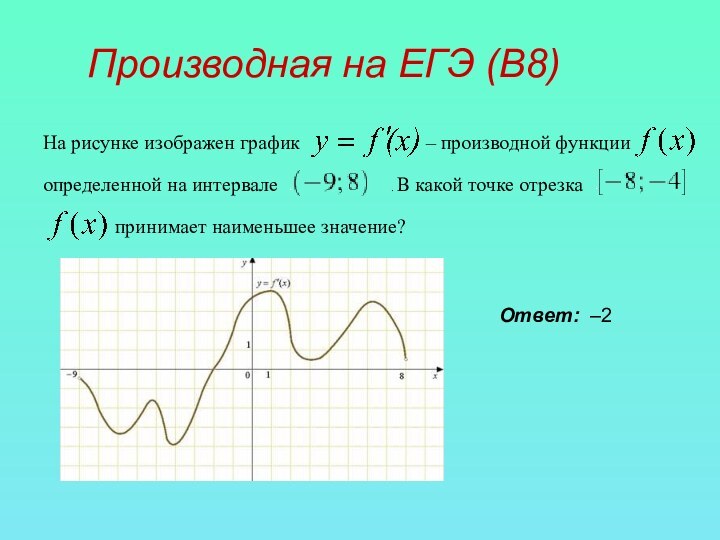
исследования
1) Находят область определения функции
2) Выясняют, является ли
функция четной (или нечетной), является ли периодической3) Находят точки пересечения функции с осями ОХ и ОУ
4) Находят промежутки знакопостоянства функции
5) Находят промежутки возрастания и убывания
6) Точки экстремума и значения функции в этих точках
7) Исследуют поведение функции в «особых» точках и при больших х (проверяют на асимптоты)