результаты освоения темы
Обоснование проекта
Учебно-тематическое планирование
Проект занятия факультатива
«Углы в пространстве» Литература
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


















Литература
Познавательные
умение анализировать, выделять главное, сравнивать, обобщать
графическую и функциональную культуру учащихся
пространственное мышление учащихся
Развивающие
показать взаимосвязь математики с окружающей действительностью
воспитание ответственного отношения к учебному труду
формирование навыков общения, умения работать в коллективе
Воспитательные
Для достижения поставленных целей в процессе обучения решаются следующие задачи:
В результате изучения темы «Метод координат в пространстве» ученик должен:
Тип урока:
комбинированный урок
Методы обучения:
объяснительный, репродуктивный, проблемный, частично-поисковый
Способ изложения
побуждает учащихся не только механически запоминать материал, но и размышлять над ним в процессе обучения
Формы обучения:
коллективная, фронтальная, индивидуальная
Средства обучения:
компьютер, проектор, экран
Проект занятия факультатива
«Старайся дать уму как можно больше пищи…»
М.В.Ломоносов
Метод координат.
Углы в пространстве.
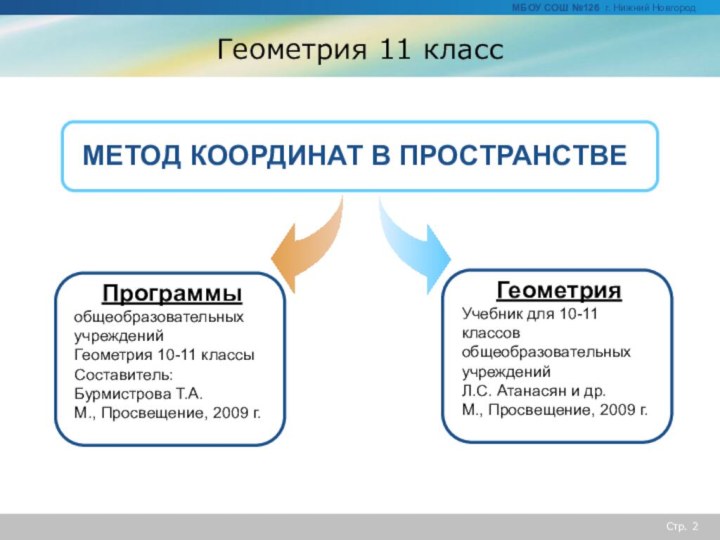
Задача: определить координаты вершин многогранников.
В каждом случае вводится прямоугольная система координат.
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), C (1,1,0),
D (0;1;0), A1 (0;0;1), B1 (1;0;1),
C1 (1;1;1), D1 (0;1;1)
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), C (1/2,√3/2,0),
A1 (0;0;1), B1 (1;0;1), C1 (1/2; √3/2,1)
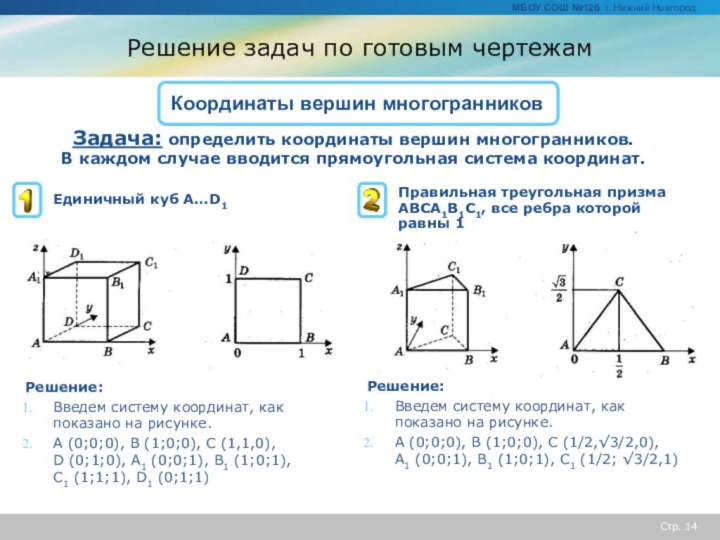
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), C (3/2,√3/2,0),
D (1;√3;0), E (0;√3;0),
F (-1/2,√3/2,0), A1 (0;0;1), B1 (1;0;1), C1 (3/2,√3/2,1), D1 (1;√3;1),
E1 (0;√3;1), F1 (-1/2,√3/2,1)
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), C (1/2,√3/2,0)
т.D проектируется в т.О – точку пересечения медиан ΔАВС, поэтому CO:ОК=2:1
ΔАOD – прямоугольный.
D (1/2;√3/6;√6/3)
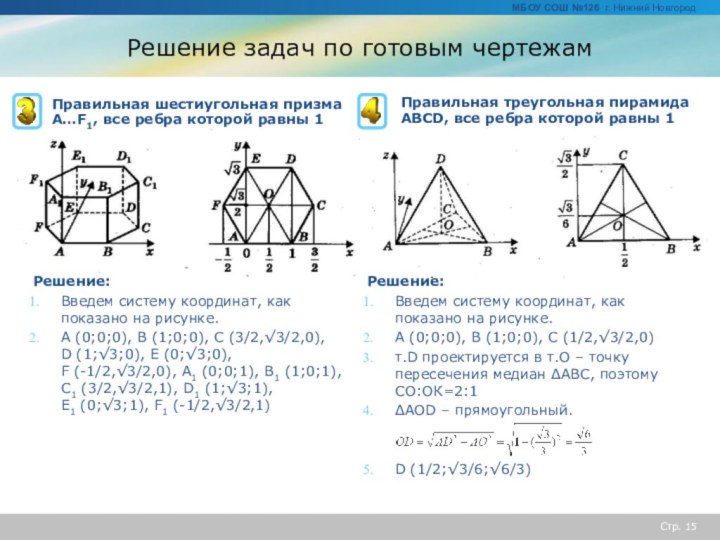
Правильная 4хугольная пирамида SABCD, все ребра которой равны 1
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), C (1,1,0),
D (0;1;0), S (1/2;1/2;√2/2)
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), C (3/2,√3/2,0),
D (1;√3;0), E (0;√3;0), F (-1/2;√3/2;0),
S (1/2;√3/2;√3)
Домашнее задание: Найти координаты вершин прямоугольного параллелепипеда, если три его измерения равны AB=6, BC=4, BB1=5.
Подведение итогов.
Ответ: 1/4
Решение:
Введем систему координат, как показано на рисунке.
A (0;0;0), B (1;0;0), D (0;1;0), S (1/2;1/2;√2/2)
AB{1;0;0} - направляющий вектор прямой АВ
(SAD): ax+by+cz+d=0 (*)
A: d=0 d=0
D: by=0 b=0
S: 1/2 a+√2/2 с=0 a =-√2c
*-√2cx+cz=0; -√2x+z=0; n{-√2;0;1} – вектор нормали (SAD)
6. ;
Ответ:
Решение задач по готовым чертежам
Угол между плоскостями
Задача: В правильном параллелепипеде А…D1, точки E и F – середины ребер B1C1 и C1D1 соответственно. AB=6, AD=4, AA1=5. Найти угол между плоскостями CEF и BDD1.
5. ;
Ответ:
Стр.