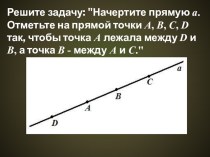
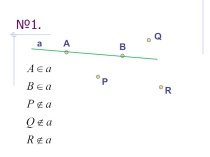
и докажем, что
А+ В+ С= 180.
Проведем через вершину
В прямую а, параллельную стороне АС. Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС. Поэтому 4= 1, 5= 3. (1)
Очевидно, сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т.е.
4+ 2+ 5=180. Отсюда, учитывая равенство (1), получаем: 1+ 2+ 3=180
или А+ В+ С= 180.
Теорема доказана.
Т
4
2
5
1
3
а
В
А
С