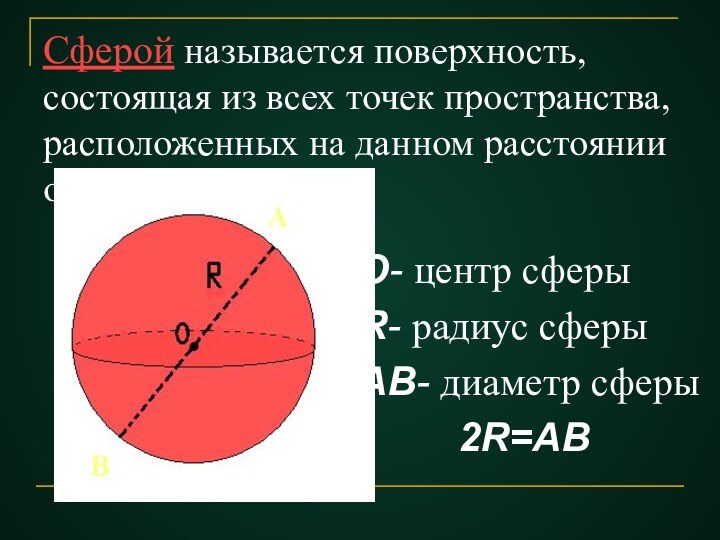
расположенных на данном расстоянии от данной точки.
О- центр сферы
R-
радиус сферыАВ- диаметр сферы
2R=АВ
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




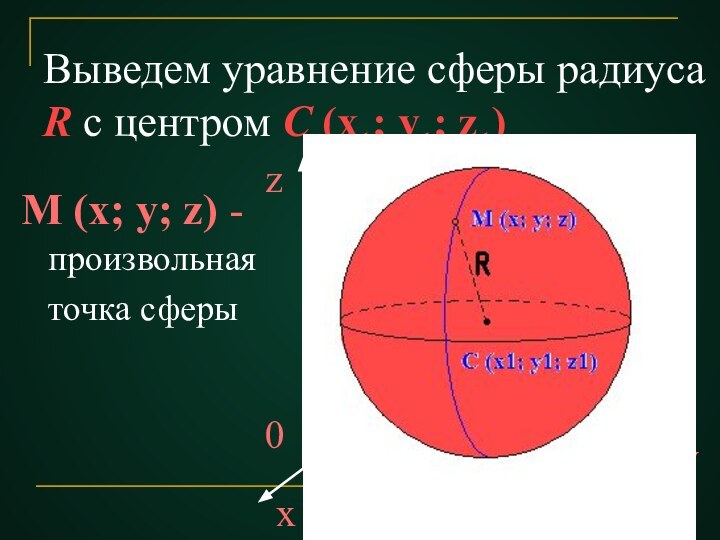













Уравнение сферы
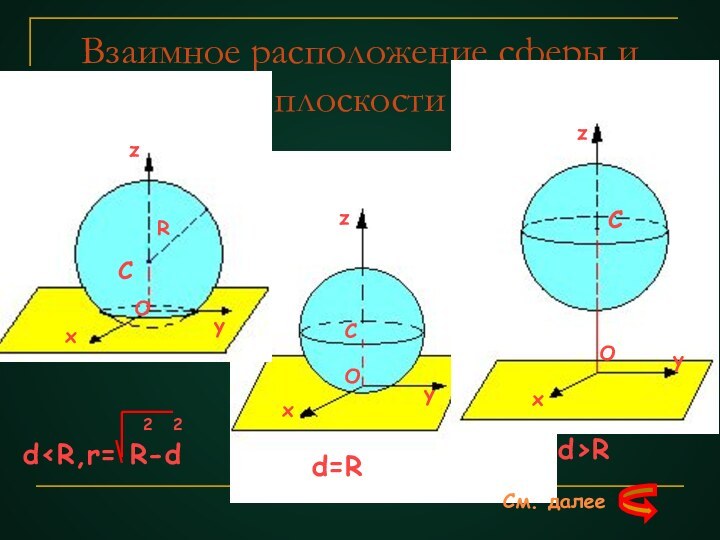
См. далее
x
z
y
0
Если точка М не лежит на данной сфере , то МС2= R2 т.е. координаты точки М не удовлетворяют данного уравнения.
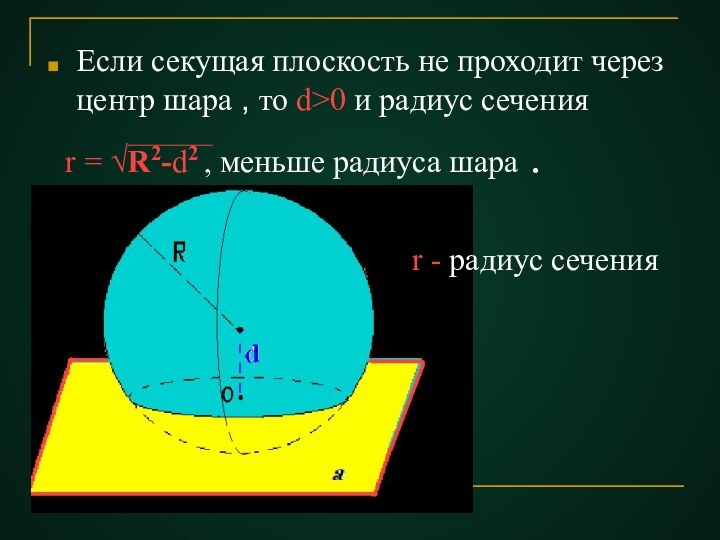
r - радиус сечения